山西省吕梁市交城县2023年中考数学模拟试卷
试卷更新日期:2023-04-18 类型:中考模拟
一、单选题
-
1. 化简的结果是( )A、2 B、 C、 D、2. 若 , 且 , 异号,则的符号为( )A、大于 B、小于 C、大于等于 D、小于等于3. 圆锥的高h、母线长l满足l=2h,底面半径为r,则其侧面展开图形的面积为( )A、πh2 B、2πh2 C、πhr2 D、πhr24. 下列计算中,正确的是( )A、 B、 C、 D、5. 如图 , 一副直角三角板和 , 将和按图放置,已知 , 在图的位置上,绕点按逆时针旋转至与重合,在旋转过程中,当与的边平行,旋转的角度是;;;;其中正确的是( )
 A、 B、 C、 D、6. 已知二次函数的顶点为 , 那么关于的一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定7. 如图,在△ABC中,AB=AC,BD=CD,点E为AC的中点,连接DE,若△ABC的周长为20cm,则△CDE的周长为( )
A、 B、 C、 D、6. 已知二次函数的顶点为 , 那么关于的一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定7. 如图,在△ABC中,AB=AC,BD=CD,点E为AC的中点,连接DE,若△ABC的周长为20cm,则△CDE的周长为( )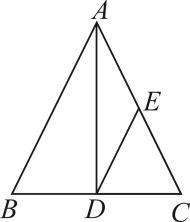 A、10 cm B、12 cm C、14 cm D、16 cm8. 下列说法正确的是( )A、有两边及一边的对角分别相等的两个三角形全等 B、有两边相等的两个直角三角形全等 C、有两个角及第三个角的对边分别相等的两个三角形全等 D、有两个角及一边相等的两个三角形全等9. 把标有号码1、2、3、4、5的5个乒乓球放在一个箱子中,摇匀后,从中任意取一个,记下号码后,放回摇匀,再从中任意取一个,则两号码之和大于2的概率是( )A、 B、 C、 D、10. 如图,△ABC是⊙O的内接三角形,AB=AC.BO的延长线交AC于点D.若∠ABD=23°.则∠A的度数为( )
A、10 cm B、12 cm C、14 cm D、16 cm8. 下列说法正确的是( )A、有两边及一边的对角分别相等的两个三角形全等 B、有两边相等的两个直角三角形全等 C、有两个角及第三个角的对边分别相等的两个三角形全等 D、有两个角及一边相等的两个三角形全等9. 把标有号码1、2、3、4、5的5个乒乓球放在一个箱子中,摇匀后,从中任意取一个,记下号码后,放回摇匀,再从中任意取一个,则两号码之和大于2的概率是( )A、 B、 C、 D、10. 如图,△ABC是⊙O的内接三角形,AB=AC.BO的延长线交AC于点D.若∠ABD=23°.则∠A的度数为( )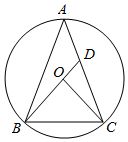 A、23° B、32° C、46° D、60°
A、23° B、32° C、46° D、60°二、填空题
-
11. 计算的结果为.12. 分解因式: .13. 写出一个不过原点,且y随x的增大而增大的函数.14. 一块材料形状是Rt△ABC,∠C=90°量得边AC=6cm,AB =10cm,用它来加工一个正方形零件,使正方形的至少一边在Rt△ABC的边上,其余顶点在其它边上,则这个正方形零件的边长为: .
 15. 如图,正方形的边长为 , 是边的中点,点是正方形内一动点, , 将线段绕点逆时针旋转得 , 连 , 线段的最小值为 .
15. 如图,正方形的边长为 , 是边的中点,点是正方形内一动点, , 将线段绕点逆时针旋转得 , 连 , 线段的最小值为 .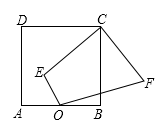
三、解答题n
-
16. 计算:17. 下面是“作一个角的平分线”的尺规作图过程.
已知:如图,钝角 . 求作:射线 , 使 .
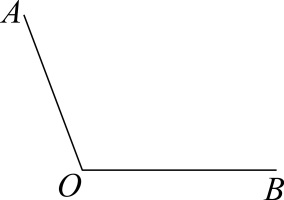
作法:
①在射线上任取一点;
②以点为圆心,长为半径作弧,交于点;
③分别以点为圆心,大于长为半径作弧,在内,两弧相交于点;
④作射线 . 则为所求作的射线.
(1)、使用直尺和圆规,补全图形(保留作图痕迹);(2)、完成下面的证明.证明:连接CD,CE,
由作图步骤②可知OD= ▲ ,
由作图步费③可知CD= ▲ ,
∵OC=OC,
∴△OCD≅△OCE.
∴∠AOC=∠BOC( )(填推理的依据).
18. 某文化用品商店准备购进甲、乙两种书包进行销售,经调查,乙书包的单价比甲书包贵元,用元购进乙书包的个数与用元购进甲书包的个数相等.(1)、求甲、乙两种书包的进价分别为多少元?(2)、商户购进甲、乙两种书包共个进行试销,其中甲书包的个数不少于个,且甲书包的个数 的倍不大于乙书包的个数,已知甲书包的售价为元/个,乙书包的售价为元/个,且 全部售出,设购进甲书包个,求该商店销售这批书包的利润与之间的函数关系式,并 写出的取值范围;(3)、在(2)的条件下,该店将个书包全部售出后,使用所获的利润又购进个书包捐赠给 贫困地区儿童,这样该商店这批书包共获利元.请求出该店第二次进货所选用的进货方案?19. 三月底,某学校迎来了以“学海通识品墨韵,开卷有益览书山”为主题的学习节活动为了让同学们更好的了解二十四节气的知识,本次学习节在沿袭以往经典项目的基础上,增设了十四节气之旅项目,并开展了相关知识竞赛该学校七、八年级各有400名学生参加了这次竞赛,现从七、八年级各随机抽取20名学生的成绩进行抽样调查.七年级:74 97 96 72 98 99 72 73 76 74 74 69 76 89 78 74 99 97 98 99
八年级:76 88 93 89 78 94 89 94 95 50 89 68 65 88 77 87 89 88 92 91
整理数据如下
成绩
人数
年级
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
七年级
0
1
10
1
a
八年级
1
2
3
8
6
分析数据如下
年级
平均数
中位数
众数
方差
七年级
84.2
77
74
138.56
八年级
84
b
89
129.7
根据以上信息,回答下列问题
(1)、a=;b=;(2)、你认为哪个年级知识竞赛的总体成绩较好,说明理由(至少从两个不同的角度说明推断的合理性).(3)、学校对知识竞赛成绩不低于80分的学生颁发优胜奖,请你估计学校七、八年级所有学生中获得优胜奖的大约有人.20. 如图,是的直径,是弦,是的半径,于点且 . 求证: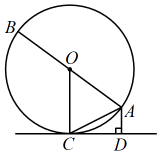 (1)、是的切线.(2)、 .21. 如图,点A表示一个半径为400米的森林公园的中心,在森林公园附近有B、C两个村庄,且∠B=45°,∠C=37°,如果在两村庄之间修一条长1000m的笔直公路将两村连通,那么该公路是否会穿过该森林公园?请说明理由.(参考数据:sin37°=0.60,cos37°=0.80,tan37°=0.75)
(1)、是的切线.(2)、 .21. 如图,点A表示一个半径为400米的森林公园的中心,在森林公园附近有B、C两个村庄,且∠B=45°,∠C=37°,如果在两村庄之间修一条长1000m的笔直公路将两村连通,那么该公路是否会穿过该森林公园?请说明理由.(参考数据:sin37°=0.60,cos37°=0.80,tan37°=0.75)