山西省晋中市昔阳县2023年中考数学质检试卷(3月份)
试卷更新日期:2023-04-18 类型:中考模拟
一、单选题
-
1. 的值为( )A、 B、1 C、 D、2. 矩形具有但菱形不一定具有的性质是( )A、对边平行且相等 B、对角相等、邻角互补 C、对角线互相垂直 D、对角线相等3. 对于反比例函数y= ,下列判断正确的是( )A、图象经过点(-1,3) B、图象在第二、四象限 C、不论x为何值,y>0 D、图象所在的第一象限内,y随x的增大而减小4. 运动会的领奖台可以近似的看成如图所示的立体图形,则它的左视图是( )
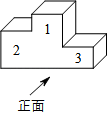 A、
A、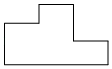 B、
B、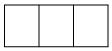 C、
C、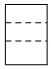 D、
D、 5. 在平面直角坐标系中,将函数的图象先向右平移1个单位长度,再向上平移5个单位长度,得到图象的函数解析式是( )A、 B、 C、 D、6. 如图,点在的边上,要判断 , 添加下列一个条件,错误的是( )
5. 在平面直角坐标系中,将函数的图象先向右平移1个单位长度,再向上平移5个单位长度,得到图象的函数解析式是( )A、 B、 C、 D、6. 如图,点在的边上,要判断 , 添加下列一个条件,错误的是( ) A、 B、 C、 D、7. 如图是冬奥会首钢滑雪大跳台赛道的剖面图,剖面图的一部分可抽象为线段 , 已知坡长为m米,坡角为α,则坡的铅垂高度为( )
A、 B、 C、 D、7. 如图是冬奥会首钢滑雪大跳台赛道的剖面图,剖面图的一部分可抽象为线段 , 已知坡长为m米,坡角为α,则坡的铅垂高度为( ) A、米 B、米 C、米 D、米8. 如图,内接于的直径,若 , 则的度数是( )
A、米 B、米 C、米 D、米8. 如图,内接于的直径,若 , 则的度数是( ) A、50° B、55° C、60° D、70°9. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b和反比例函数y= 在同一平面直角坐标系中的图象可能是( )
A、50° B、55° C、60° D、70°9. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b和反比例函数y= 在同一平面直角坐标系中的图象可能是( )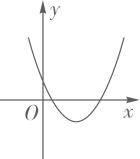 A、
A、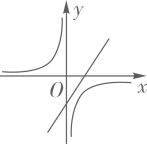 B、
B、 C、
C、 D、
D、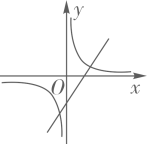 10. 如图,扇形纸片的半径为2,沿折叠扇形纸片,点O恰好落在上的点C处,图中阴影部分的面积为( )
10. 如图,扇形纸片的半径为2,沿折叠扇形纸片,点O恰好落在上的点C处,图中阴影部分的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 二次函数的顶点坐标是 .12. 如图,在菱形中,对角线与相交于点 , , , 则菱形的面积为 .
 13. 如图,的顶点在正方形网格的格点上,则的值为 .
13. 如图,的顶点在正方形网格的格点上,则的值为 . 14. 如图,四边形ABCD内接于☉O,四边形ABCO是平行四边形,则∠ADC=°
14. 如图,四边形ABCD内接于☉O,四边形ABCO是平行四边形,则∠ADC=° 15. 如图所示,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数在第一象限内的图象经过点D,交BC于点E.若 , 则k的值为 .
15. 如图所示,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数在第一象限内的图象经过点D,交BC于点E.若 , 则k的值为 .
三、解答题
-
16.(1)、计算: .(2)、下面是小明同学解方程的过程,请认真阅读并完成相应的任务.
解:
第一步
, 即第二步
第三步
第四步
任务一:
①填空:上述材料中小明同学解一元二次方程的数学方法是 ▲ , 依据的一个数学公式是 ▲ ;第 ▲ 步开始出现错误;
任务二:
②请你直接写出该方程的正确解.
17. “航天知识竞赛”活动中,获得“小宇航员”称号的小颖得到了A,B,C,D四枚纪念章(除图案外完全相同),如图所示,四枚纪念章上分别印有“嫦娥五号”、“天问一号”、“长征火箭”和“天宫一号”的图案.她将这四枚纪念章背面朝上放在桌面上,然后从中随机选取两枚送给同学小彬,求小颖送给小彬的两枚纪念章中恰好有一枚印有“嫦娥五号”图案的概率(请用“画树状图”或“列表”等方法写出分析过程).A.嫦娥五号
 B.天问一号
B.天问一号
C.长征火箭
 D.天宫一号
D.天宫一号 18. 如图,一次函数的图象与反比例函数(k为常数,)的图象交于A、B两点,B点的坐标为 .
18. 如图,一次函数的图象与反比例函数(k为常数,)的图象交于A、B两点,B点的坐标为 . (1)、求两个函数的表达式和A点坐标;(2)、根据图象直接写出当时,自变量x的取值范围.19. “眉山水街”走红网络,成为全国各地不少游客新的打卡地!游客小何用无人机对该地一标志建筑物进行拍摄和观测,如图,无人机从 处测得该建筑物顶端 的俯角为24°,继续向该建筑物方向水平飞行20米到达 处,测得顶端 的俯角为45°,已知无人机的飞行高度为60米,则这栋建筑物的高度是多少米?(精确到0.1米,参考数据: , , )
(1)、求两个函数的表达式和A点坐标;(2)、根据图象直接写出当时,自变量x的取值范围.19. “眉山水街”走红网络,成为全国各地不少游客新的打卡地!游客小何用无人机对该地一标志建筑物进行拍摄和观测,如图,无人机从 处测得该建筑物顶端 的俯角为24°,继续向该建筑物方向水平飞行20米到达 处,测得顶端 的俯角为45°,已知无人机的飞行高度为60米,则这栋建筑物的高度是多少米?(精确到0.1米,参考数据: , , )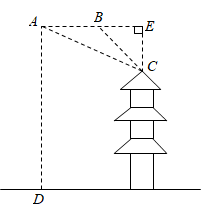 20. 2022北京冬奥会期间,冰墩墩和雪容融受到人们的广泛喜爱.某网店以每套96元的价格购进了一批冰墩墩和雪容融,由于销售火爆,销售单价经过两次的调整,从每套150元上涨到每套216元,此时每天可售出16套冰墩墩和雪容融.
20. 2022北京冬奥会期间,冰墩墩和雪容融受到人们的广泛喜爱.某网店以每套96元的价格购进了一批冰墩墩和雪容融,由于销售火爆,销售单价经过两次的调整,从每套150元上涨到每套216元,此时每天可售出16套冰墩墩和雪容融.
 (1)、若销售价格每次上涨的百分率相同,求每次上涨的百分率;(2)、预计冬奥会闭幕后需求会有所下降,需尽快将这批冰墩墩和雪容融售出,决定降价出售.经过市场调查发现:销售单价每降价10元,每天多卖出2套,当降价钱数m为多少元时每天的利润W(元)可达到最大,最大利润是多少?21. 阅读与思考
(1)、若销售价格每次上涨的百分率相同,求每次上涨的百分率;(2)、预计冬奥会闭幕后需求会有所下降,需尽快将这批冰墩墩和雪容融售出,决定降价出售.经过市场调查发现:销售单价每降价10元,每天多卖出2套,当降价钱数m为多少元时每天的利润W(元)可达到最大,最大利润是多少?21. 阅读与思考如图是小宇同学的错题积累本的部分内容,请仔细阅读,并完成相应的任务.
×年×月×日星期日错题积累
在中,平分交于点D,O是上一点,且经过B,D两点,分别交于点E,F.
…

【自勉】
读书使人头脑充实,讨论使人明辨是非,做笔记则能使知识精确.
——培根
任务:
(1)、使用直尺和圆规,根据题目要求补全图形(不写作法,保留作图痕迹);(2)、求证:与相切于点D;(3)、若 , 则劣弧的长为 .22. 综合与实践:问题情境:如图1,在正方形中,点E是对角线上一点,连接 , 过点E分别作的垂线,分别交直线于点F,G.试猜想线段的数量关系并加以证明.
 (1)、数学思考:
(1)、数学思考:请解答上述问题;
(2)、问题解决:如图2,在图1的条件下,将“正方形”改为“矩形”,其他条件不变.若 , , 求的值;
(3)、问题拓展:在(2)的条件下,当点E为的中点时,请直接写出的面积.
23. 在平面直角坐标系中,二次函数的图象与x轴交于两点,与y轴交于点C. (1)、求这个二次函数的解析式;(2)、点P是直线上方的抛物线上一动点,设三角形的面积为S,求S的最大值及S取得最大值时点P的坐标;(3)、点M为抛物线上一动点,在x轴上是否存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.
(1)、求这个二次函数的解析式;(2)、点P是直线上方的抛物线上一动点,设三角形的面积为S,求S的最大值及S取得最大值时点P的坐标;(3)、点M为抛物线上一动点,在x轴上是否存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.