山东省聊城市临清市2023年中考一模数学试题
试卷更新日期:2023-04-18 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、 B、25 C、 D、2. 1微米 , 一根头发丝的直径约为50微米,50微米用科学记数法可以表示为( )A、 B、 C、 D、3. 下列图形,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 已知点A(1﹣2x,x﹣1)在第二象限,则x的取值范围在数轴上表示正确的是( )A、
4. 下列运算正确的是( )A、 B、 C、 D、5. 已知点A(1﹣2x,x﹣1)在第二象限,则x的取值范围在数轴上表示正确的是( )A、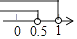 B、
B、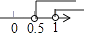 C、
C、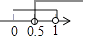 D、
D、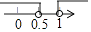 6. 一个由完全相同的小正方体组成的几何体的三视图如图所示,若在这个几何体的基础上增加几个相同的小正方体,将其补成一个大正方体,则需要增加的小正方体的个数最少为( )
6. 一个由完全相同的小正方体组成的几何体的三视图如图所示,若在这个几何体的基础上增加几个相同的小正方体,将其补成一个大正方体,则需要增加的小正方体的个数最少为( ) A、6个 B、5个 C、4个 D、3个7. 若α,β是方程的两个实数根,则代数式的值为( )A、 B、 C、2011 D、20238. 某中学对学生最喜欢的课外活动进行了随机抽样调查,要求每人只能选择其中的一项.根据得到的数据,绘制的不完整统计图如下,则下列说法中错误的是( )
A、6个 B、5个 C、4个 D、3个7. 若α,β是方程的两个实数根,则代数式的值为( )A、 B、 C、2011 D、20238. 某中学对学生最喜欢的课外活动进行了随机抽样调查,要求每人只能选择其中的一项.根据得到的数据,绘制的不完整统计图如下,则下列说法中错误的是( ) A、这次调查的样本容量是200 B、全校1600名学生中,估计最喜欢体育课外活动的大约有500人 C、扇形统计图中,科技部分所对应的圆心角是 D、被调查的学生中,最喜欢艺术课外活动的有50人9. 如图,中,弦 , 相交于点P,若 , , 则等于( )
A、这次调查的样本容量是200 B、全校1600名学生中,估计最喜欢体育课外活动的大约有500人 C、扇形统计图中,科技部分所对应的圆心角是 D、被调查的学生中,最喜欢艺术课外活动的有50人9. 如图,中,弦 , 相交于点P,若 , , 则等于( ) A、 B、 C、 D、10. 二次函数的图象如图所示,那么一次函数与反比例函数在同一平面直角坐标系中的图象大致是( )
A、 B、 C、 D、10. 二次函数的图象如图所示,那么一次函数与反比例函数在同一平面直角坐标系中的图象大致是( ) A、
A、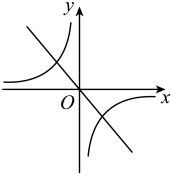 B、
B、 C、
C、 D、
D、 11. 如图,在平行四边形中,E为上一点,且 , 与相交于点F, , 则为( )
11. 如图,在平行四边形中,E为上一点,且 , 与相交于点F, , 则为( ) A、9 B、12 C、27 D、3612. 将两个等腰直角三角形与(其中 , , )如图放置在一起,点在上,与交于点 , 连接 , , 且 , 下列结论:
A、9 B、12 C、27 D、3612. 将两个等腰直角三角形与(其中 , , )如图放置在一起,点在上,与交于点 , 连接 , , 且 , 下列结论:①垂直平分;②为等边三角形;③;④ . 正确的结论是( )
 A、只有①② B、只有①②③ C、只有①③④ D、①②③④
A、只有①② B、只有①②③ C、只有①③④ D、①②③④二、填空题
-
13. 分解因式:4a﹣a3=.14. 如图,在中, , 将绕点顺时针旋转到的位置,点E恰好落在边上,且 , 则的度数为 .
 15. 如图,将半径为的圆形纸片剪去圆周的一个扇形,用剩下的扇形围成一个圆锥的侧面(接缝忽略不计),这个圆锥的高是 .
15. 如图,将半径为的圆形纸片剪去圆周的一个扇形,用剩下的扇形围成一个圆锥的侧面(接缝忽略不计),这个圆锥的高是 .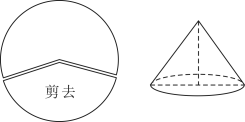 16. 看了《田忌赛马》故事后,小杨用数学模型来分析齐王与田忌的上中下三个等级的三匹马记分如表,每匹马只赛一场,两数相比,大数为胜,三场两胜则赢.已知齐王的三匹马出场顺序为10,8,6.若田忌的三匹马随机出场,则田忌能赢得比赛的概率为 .
16. 看了《田忌赛马》故事后,小杨用数学模型来分析齐王与田忌的上中下三个等级的三匹马记分如表,每匹马只赛一场,两数相比,大数为胜,三场两胜则赢.已知齐王的三匹马出场顺序为10,8,6.若田忌的三匹马随机出场,则田忌能赢得比赛的概率为 .马匹
姓名
下等马
中等马
上等马
齐王
6
8
10
田忌
5
7
9
17. 如图,点 , 是正方形的两个顶点,以对角线为边作正方形 , 再以对角线为边作正方形 , …,依此规律,点的坐标是 .
三、解答题
-
18. 化简求值: , 其中 .19. 为庆祝中国共产党建党100周年,某校举行了“红色华诞,党旗飘扬”党史知识竞赛.为了解竞赛成绩,抽样调查了七,八年级部分学生的分数,过程如下:
收集数据从该校七、八年级学生中各随机抽取20名学生的分数,其中八年级的分数如下:81 83 84 85 86 87 87 88 89 90
92 92 93 95 95 95 99 99 100 100
整理、描述数据按如下分段整理描述样本数据:分数
人数
年级
七年级
4
6
2
8
八年级
3
4
7
分析数据两组样本数据的平均数、中位数、众数、方差如下表所示:
年级
平均数
中位数
众数
方差
七年级
91
89
97
40.9
八年级
91
33.2
根据以上提供的信息,解答下列问题:
①填空: , , ;
②样本数据中,七年级甲同学和八年级乙同学的分数都为90分,同学的分数在本年级抽取的分数中从高到低排序更靠前(填“甲”或“乙”):
③从样本数据分析来看,分数较整齐的是年级(填“七”或“八”);
④如果七年级共有400人参赛,则该年级约有人的分数不低于95分.
20. 如图,平行四边形ABCD的对角线AC、BD相交于点O,AF=CE. (1)、求证:△BAE≌△DCF;(2)、若BD⊥EF,连接DE、BF,判断四边形EBFD的形状,并说明理由.21. 昌云中学计划为地理兴趣小组购买大、小两种地球仪,若购买1个大地球仪和3个小地球仪需要136元;若购买2个大地球仪和1个小地球仪需要132元.(1)、求每个大地球仪和每个小地球仪各多少元;(2)、昌云中学决定购买以上两种地球仪共30个,总费用不超过960元,那么昌云中学最多可以购买多少个大地球仪.22. 数学兴趣小组到一公园测量塔楼高度.如图所示,塔楼剖面和台阶的剖面在同一平面,在台阶底部点A处测得塔楼顶端点E的仰角 , 台阶AB长26米,台阶坡面AB的坡度 , 然后在点B处测得塔楼顶端点E的仰角 , 则塔顶到地面的高度EF约为多少米.
(1)、求证:△BAE≌△DCF;(2)、若BD⊥EF,连接DE、BF,判断四边形EBFD的形状,并说明理由.21. 昌云中学计划为地理兴趣小组购买大、小两种地球仪,若购买1个大地球仪和3个小地球仪需要136元;若购买2个大地球仪和1个小地球仪需要132元.(1)、求每个大地球仪和每个小地球仪各多少元;(2)、昌云中学决定购买以上两种地球仪共30个,总费用不超过960元,那么昌云中学最多可以购买多少个大地球仪.22. 数学兴趣小组到一公园测量塔楼高度.如图所示,塔楼剖面和台阶的剖面在同一平面,在台阶底部点A处测得塔楼顶端点E的仰角 , 台阶AB长26米,台阶坡面AB的坡度 , 然后在点B处测得塔楼顶端点E的仰角 , 则塔顶到地面的高度EF约为多少米.(参考数据: , , , )
 23. 如图,矩形的顶点O与坐标原点重合,点C在x轴上,点A在对角线OB上,且 , . 反比例函数的图象经过点A,交 , 于点M,N, , 连接 , , .
23. 如图,矩形的顶点O与坐标原点重合,点C在x轴上,点A在对角线OB上,且 , . 反比例函数的图象经过点A,交 , 于点M,N, , 连接 , , . (1)、求反比例函数的解析式及点N的坐标;(2)、若点P在x轴上,且的面积与四边形的面积相等,求点P的坐标.24. 如图,的弦 , 交于点E,连接 , , 延长到点P,连结 , 与相切,且 .
(1)、求反比例函数的解析式及点N的坐标;(2)、若点P在x轴上,且的面积与四边形的面积相等,求点P的坐标.24. 如图,的弦 , 交于点E,连接 , , 延长到点P,连结 , 与相切,且 .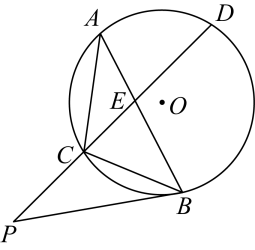 (1)、求证:点A是的中点;(2)、若 , , 求的长.25. 抛物线与x轴交于A,B两点,与y轴交于点C,点B的坐标为 , 抛物线的对称轴为 , 直线AD交抛物线于点 .
(1)、求证:点A是的中点;(2)、若 , , 求的长.25. 抛物线与x轴交于A,B两点,与y轴交于点C,点B的坐标为 , 抛物线的对称轴为 , 直线AD交抛物线于点 . (1)、求抛物线和直线的解析式;(2)、如图1,点Q是线段上一动点,过点Q作 , 交于点E,连接 , 若点Q的坐标为 , 求的面积S与m的函数表达式,并写出S是否存在最大值?若存在,求出S的最大值,并直接写出此时点E的坐标;(3)、如图2,直线交y轴于点F,点M为抛物线对称轴上的动点,点N在x轴上,当四边形周长取最小值时,求出满足条件的点M和点N的坐标.
(1)、求抛物线和直线的解析式;(2)、如图1,点Q是线段上一动点,过点Q作 , 交于点E,连接 , 若点Q的坐标为 , 求的面积S与m的函数表达式,并写出S是否存在最大值?若存在,求出S的最大值,并直接写出此时点E的坐标;(3)、如图2,直线交y轴于点F,点M为抛物线对称轴上的动点,点N在x轴上,当四边形周长取最小值时,求出满足条件的点M和点N的坐标.