山东省聊城市冠县2023年中考一模数学试题
试卷更新日期:2023-04-18 类型:中考模拟
一、单选题
-
1. 下列实数为无理数的是( )A、 B、0.2 C、 D、2. 化简的结果是( )A、 B、 C、 D、03. 下列图形是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、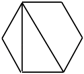 4. 如图,直线 , 截线c,d相交成角, , 则的度数是( )
4. 如图,直线 , 截线c,d相交成角, , 则的度数是( ) A、 B、 C、 D、5. 一组数据:3,4,4,6,若添加一个数据6,则不发生变化的统计量是( )A、平均数 B、中位数 C、众数 D、方差6. 若是方程的一个根,则此方程的另一个根是( )A、 B、0 C、3 D、47. 如图所示的几何体是由5个大小相同的小立方块搭成的,它的主视图是( )
A、 B、 C、 D、5. 一组数据:3,4,4,6,若添加一个数据6,则不发生变化的统计量是( )A、平均数 B、中位数 C、众数 D、方差6. 若是方程的一个根,则此方程的另一个根是( )A、 B、0 C、3 D、47. 如图所示的几何体是由5个大小相同的小立方块搭成的,它的主视图是( )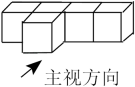 A、
A、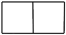 B、
B、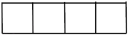 C、
C、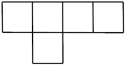 D、
D、 8. 如图,是由12个全等的等边三角形组成的图案,假设可以随机在图中取点,那么这个点取在阴影部分的概率是( )
8. 如图,是由12个全等的等边三角形组成的图案,假设可以随机在图中取点,那么这个点取在阴影部分的概率是( )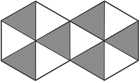 A、 B、 C、 D、9. 如图, , , 是上的三点,若 , 则的度数是( )
A、 B、 C、 D、9. 如图, , , 是上的三点,若 , 则的度数是( ) A、 B、 C、 D、10. 如图是关于的一个函数图象,根据图象,下列说法正确的是( )
A、 B、 C、 D、10. 如图是关于的一个函数图象,根据图象,下列说法正确的是( ) A、该函数的最大值为7 B、当时,随的增大而增大 C、当时,对应的函数值 D、当和时,对应的函数值相等11. 有一个正n边形旋转后与自身重合,则n为( )A、6 B、9 C、12 D、1512. 如图,在一个单位面积为1的方格纸上, , , , ……是斜边在x轴上,且斜边长分别为2,4,6,……的等腰直角三角形.若的顶点坐标分别为 , , , 则依图中所示规律,则的坐标是( )
A、该函数的最大值为7 B、当时,随的增大而增大 C、当时,对应的函数值 D、当和时,对应的函数值相等11. 有一个正n边形旋转后与自身重合,则n为( )A、6 B、9 C、12 D、1512. 如图,在一个单位面积为1的方格纸上, , , , ……是斜边在x轴上,且斜边长分别为2,4,6,……的等腰直角三角形.若的顶点坐标分别为 , , , 则依图中所示规律,则的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 因式分解: .14. 下图是根据甲、乙两城市一周的日均气温绘制的折线统计图,根据统计图判断本圈的日平均气温较稳定的城市是 . (选填“甲”或“乙”)
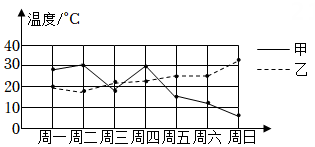 15. 如图,边长为4的正方形ABCD内接于 , 则的长是(结果保留)
15. 如图,边长为4的正方形ABCD内接于 , 则的长是(结果保留) 16. 一副三角板如图摆放,直线 , 则的度数是 .
16. 一副三角板如图摆放,直线 , 则的度数是 . 17. 如图,有一张平行四边形纸片 , , , 将这张纸片折叠,使得点落在边上,点的对应点为点 , 折痕为 , 若点在边上,则长的最小值等于 .
17. 如图,有一张平行四边形纸片 , , , 将这张纸片折叠,使得点落在边上,点的对应点为点 , 折痕为 , 若点在边上,则长的最小值等于 .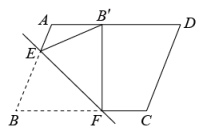
三、解答题
-
18. 解不等式组: , 并写出它的正整数解.19. 如图,点D,E分别在边 , 上,且 , 连接 , . . 求证:是等腰三角形.
 20. 某校在九年级学生中随机抽取了若干名学生参加“平均每天体育运动时间”的调查,根据调查结果绘制了如下不完整的频数分布表和频数分布直方图.
20. 某校在九年级学生中随机抽取了若干名学生参加“平均每天体育运动时间”的调查,根据调查结果绘制了如下不完整的频数分布表和频数分布直方图.频数分布表
运动时间t/min
频数
频率
4
0.1
7
0.175
a
0.35
9
0.225
6
b
合计
n
1
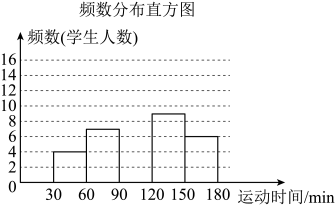
请根据图表中的信息解答下列问题:
(1)、频数分布表中的a= , b= , n=;(2)、请补全频数分布直方图;(3)、若该校九年级共有480名学生,试估计该校九年级学生平均每天体育运动时间不低于120 min的学生人数.21. 如图,湖边、两点由两段笔直的观景栈道和相连.为了计算、两点之间的距离,经测量得: , , 米,求、两点之间的距离.(参考数据: , , , , , ) 22. 某学校打算购买甲乙两种不同类型的笔记本.已知甲种类型的笔记本的单价比乙种类型的要便宜1元,且用110元购买的甲种类型的数量与用120元购买的乙种类型的数量一样.(1)、求甲乙两种类型笔记本的单价.(2)、该学校打算购买甲乙两种类型笔记本共100件,且购买的乙的数量不超过甲的3倍,则购买的最低费用是多少?23. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于点 , 与轴交于点 .
22. 某学校打算购买甲乙两种不同类型的笔记本.已知甲种类型的笔记本的单价比乙种类型的要便宜1元,且用110元购买的甲种类型的数量与用120元购买的乙种类型的数量一样.(1)、求甲乙两种类型笔记本的单价.(2)、该学校打算购买甲乙两种类型笔记本共100件,且购买的乙的数量不超过甲的3倍,则购买的最低费用是多少?23. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于点 , 与轴交于点 .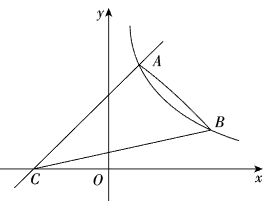 (1)、求点的坐标和反比例函数的解析式;(2)、点是反比例函数图象上一点且纵坐标是1,连接 , , 求的面积.
(1)、求点的坐标和反比例函数的解析式;(2)、点是反比例函数图象上一点且纵坐标是1,连接 , , 求的面积.
