山东省济南市长清区2023年(东片区)中考一模数学试题
试卷更新日期:2023-04-18 类型:中考模拟
一、单选题
-
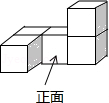
1. 的倒数是( )A、 B、3 C、 D、2. 如图是一个由5个完全相同的小正方体组成的立体图形,它的俯视图是( )
 A、
A、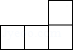 B、
B、 C、
C、 D、
D、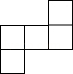 3. 中国空间站俯瞰地球的高度约为400000米,将400000用科学记数法表示应为( )A、 B、 C、 D、4.
3. 中国空间站俯瞰地球的高度约为400000米,将400000用科学记数法表示应为( )A、 B、 C、 D、4.如图,将三角板的直角顶点放在两条平行线a、b中的直线b上,如果∠1=40°,则∠2的度数是()
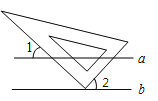 A、30° B、45° C、40° D、50°5. 位于四川省的三星堆遗址被称为20世纪人类最伟大的考古发现之一,其中出土的文物是宝贵的人类文化遗产,在中国的文物群体中,属最具历史、科学、文化、艺术价值和最富观赏性的文物群体之一.下列四个图案是三星堆遗址出土文物图,其中是中心对称图形的是( )A、
A、30° B、45° C、40° D、50°5. 位于四川省的三星堆遗址被称为20世纪人类最伟大的考古发现之一,其中出土的文物是宝贵的人类文化遗产,在中国的文物群体中,属最具历史、科学、文化、艺术价值和最富观赏性的文物群体之一.下列四个图案是三星堆遗址出土文物图,其中是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 2023年春节期间,全国各地迎来了旅游热潮,小丽和小希计划趁着寒假在省内结伴游玩.出发之前,两人用随机抽卡片的方式来决定去哪个景点旅游,于是两人制作了四张材质和外观完全一样的卡片,每张卡片的正面绘有一张景点图,将这四张卡片背面朝上洗匀,小丽随机抽取一张后放回,小希再随机抽取一张,则两人抽到的景点相同的概率是( )
6. 2023年春节期间,全国各地迎来了旅游热潮,小丽和小希计划趁着寒假在省内结伴游玩.出发之前,两人用随机抽卡片的方式来决定去哪个景点旅游,于是两人制作了四张材质和外观完全一样的卡片,每张卡片的正面绘有一张景点图,将这四张卡片背面朝上洗匀,小丽随机抽取一张后放回,小希再随机抽取一张,则两人抽到的景点相同的概率是( )


 A、 B、 C、 D、7. 如图,在中, , . 以点C为中心,把逆时针旋转 , 得到 , 则图中阴影部分的面积为( )
A、 B、 C、 D、7. 如图,在中, , . 以点C为中心,把逆时针旋转 , 得到 , 则图中阴影部分的面积为( )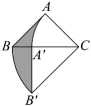 A、2 B、 C、4 D、8. 如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,3 ),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( )
A、2 B、 C、4 D、8. 如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,3 ),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( )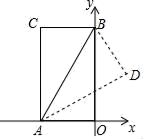 A、( , ) B、(2, ) C、( , ) D、( ,3﹣ )9. 已知二次函数 (a,b是常数, )的图象经过 , , 三个点中的其中两个点.平移该函数的图象,使其顶点始终在直线 上,则平移后所得抛物线与y轴交点纵坐标的( )A、最大值为 B、最小值为 C、最大值为 D、最小值为
A、( , ) B、(2, ) C、( , ) D、( ,3﹣ )9. 已知二次函数 (a,b是常数, )的图象经过 , , 三个点中的其中两个点.平移该函数的图象,使其顶点始终在直线 上,则平移后所得抛物线与y轴交点纵坐标的( )A、最大值为 B、最小值为 C、最大值为 D、最小值为二、填空题
-
10. 分解因式: .11. 如图,转盘中6个扇形的面积都相等.任意转动转盘1次,当转盘停止转动时(指向两个扇形交线处时,重新转动转盘),事件“指针落在蓝色扇形中”的概率为.
 12. 若一个多边形的每个内角都为 , 则它的边数为 .13. 代数式 与代数式 的和为4,则 .14. AB两地相距20km,甲从A地出发向B地前进,乙从B地出发向A地前进,两人沿同一直线同时出发,甲先以8km/h的速度前进1小时,然后减慢速度继续匀速前进,甲乙两人离A地的距离S(km)与时间t(h)的关系如图所示,则甲出发小时后与乙相遇.
12. 若一个多边形的每个内角都为 , 则它的边数为 .13. 代数式 与代数式 的和为4,则 .14. AB两地相距20km,甲从A地出发向B地前进,乙从B地出发向A地前进,两人沿同一直线同时出发,甲先以8km/h的速度前进1小时,然后减慢速度继续匀速前进,甲乙两人离A地的距离S(km)与时间t(h)的关系如图所示,则甲出发小时后与乙相遇.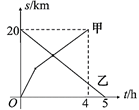 15. 如图,矩形中,E为边上一点,将沿折叠,使点A的对应点F恰好落在边上,连接交于点N,连接 . 若 , , 则矩形的面积为 .
15. 如图,矩形中,E为边上一点,将沿折叠,使点A的对应点F恰好落在边上,连接交于点N,连接 . 若 , , 则矩形的面积为 .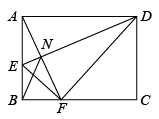
三、解答题
-
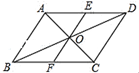
16. 计算: .17. 解不等式组: , 并写出的所有整数解.18. 如图,在▱ABCD 中,对角线 AC,BD 相交于点 O,过点 O 的一条直线分别交 AD,BC 于点 E,F.求证:AE=CF.
 19. 中华文化源远流长,文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”某中学为了解学生对四大名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如下尚不完整的统计图.
19. 中华文化源远流长,文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”某中学为了解学生对四大名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如下尚不完整的统计图.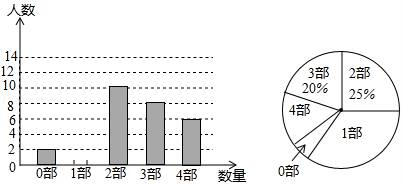
请根据以上信息,解决下列问题
(1)、本次调查所得数据的众数是部,中位数是部;(2)、扇形统计图中“4部”所在扇形的圆心角为度;(3)、请将条形统计图补充完整;(4)、没有读过四大古典名著的两名学生准备从中各自随机选择一部来阅读,求他们恰好选中同一名著的概率.20. 如图,某无人机兴趣小组在操场上开展活动,此时无人机在离地面30米的D处,无人机测得操控者A的俯角为30°,测得教学楼BC顶端点C处的俯角为45°.又经过人工测量测得操控者A和教学楼BC之间的距离为57米.求教学楼BC的高度.(点A,B,C,D都在同一平面上,结果保留根号)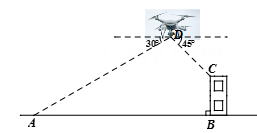 21. 如图,在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过D作⊙O的切线交AB的延长线于E,交BC于F.
21. 如图,在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过D作⊙O的切线交AB的延长线于E,交BC于F. (1)、求证:DF⊥BC;(2)、求证:DE2=AE•BE.22. 某社区在防治新型冠状病毒期间,需要购进一批防护服,现有甲、乙两种不同型号的防护服,已知每件甲型防护服的价格比每件乙型防护服的价格便宜30元,用4200元购买甲型防护服的件数与用5250元购买乙型防护服的件数刚好相等.(1)、求甲、乙两种型号的防护服每件各是多少元?(2)、如果该社区计划购进的防护服共需80件,且要求投入的经费不超过11400元,则最多可购买多少件乙型防护服?23. 如图1,直线l与坐标轴的正半轴分别交于A,B两点,与反比例函数()的图像交于C,D两点(点C在点D的左边),过点C作轴于点E,过点D作轴于点F,与交于点G(4,3).
(1)、求证:DF⊥BC;(2)、求证:DE2=AE•BE.22. 某社区在防治新型冠状病毒期间,需要购进一批防护服,现有甲、乙两种不同型号的防护服,已知每件甲型防护服的价格比每件乙型防护服的价格便宜30元,用4200元购买甲型防护服的件数与用5250元购买乙型防护服的件数刚好相等.(1)、求甲、乙两种型号的防护服每件各是多少元?(2)、如果该社区计划购进的防护服共需80件,且要求投入的经费不超过11400元,则最多可购买多少件乙型防护服?23. 如图1,直线l与坐标轴的正半轴分别交于A,B两点,与反比例函数()的图像交于C,D两点(点C在点D的左边),过点C作轴于点E,过点D作轴于点F,与交于点G(4,3). (1)、当点D恰好是中点时,求此时点C的横坐标;(2)、如图2,连接 , 求证:;(3)、如图3,将沿折叠,点G恰好落在边上的点H处,求此时反比例函数的解析式.24. 在学习了图形的旋转知识后,数学兴趣小组的同学们又进一步对图形旋转前后的线段之间、角之间的关系进行了探究.
(1)、当点D恰好是中点时,求此时点C的横坐标;(2)、如图2,连接 , 求证:;(3)、如图3,将沿折叠,点G恰好落在边上的点H处,求此时反比例函数的解析式.24. 在学习了图形的旋转知识后,数学兴趣小组的同学们又进一步对图形旋转前后的线段之间、角之间的关系进行了探究.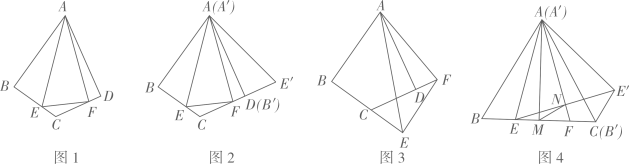
(一)尝试探究:如图1,在四边形ABCD中,AB=AD,∠BAD=60°,∠ABC=∠ADC=90°,点E、F分别在线段BC、CD上,∠EAF=30°,连接EF.
(1)、如图2,将△ABE绕点A逆时针旋转60°后得到△A′B′E′(A′B′与AD重合),请直接写出∠E′AF=度,线段BE、EF、FD之间的数量关系为 .(2)、如图3,当但点E、F分别在线段BC、CD的延长线上时,其他条件不变,请探究线段BE、EF、FD之间的数量关系,并说明理由.(3)、拓展延伸:如图4,在等边△ABC中,E、F是边BC上的两点,∠EAF=30°,BE=1,将△ABE绕点A逆时针旋转60°得到△A′B′E′(A′B′与AC重合),连接EE′,AF与EE′交于点N,过点A作AM⊥BC于点M,连接MN,求线段MN的长度.25. 已知抛物线y=ax2+bx+3经过点A (1,0)和点B (-3,0),与y轴交于点C,点P为第二象限内抛物线上的动点.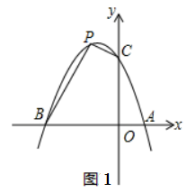

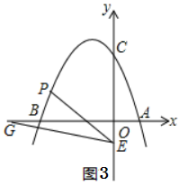 (1)、抛物线的解析式为 , 抛物线的顶点坐标为;(2)、如图1,是否存在点P,使四边形BOCP的面积为8?若存在,请求出点P的坐标;若不存在,请说明理由.(3)、如图2,连接OP交BC于点D,当S△CPD∶S△BPD=1∶2时,请求出点D的坐标;(4)、如图3,点E的坐标为(0,-1),点G为x轴负半轴上的一点,∠OGE=15°,连接PE,若∠PEG=2∠OGE,请求出点P的坐标.
(1)、抛物线的解析式为 , 抛物线的顶点坐标为;(2)、如图1,是否存在点P,使四边形BOCP的面积为8?若存在,请求出点P的坐标;若不存在,请说明理由.(3)、如图2,连接OP交BC于点D,当S△CPD∶S△BPD=1∶2时,请求出点D的坐标;(4)、如图3,点E的坐标为(0,-1),点G为x轴负半轴上的一点,∠OGE=15°,连接PE,若∠PEG=2∠OGE,请求出点P的坐标.