山东省菏泽市郓城县2023年九年级下学期第一次模拟数学考试
试卷更新日期:2023-04-18 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 据测算,世博会召开时,上海使用清洁能源可减少二氧化碳排放约16万吨,将16万吨用科学记数法表示为( )A、1.6×103吨 B、1.6×104吨 C、1.6×105吨 D、1.6×106吨3. 现实世界中,对称现象无处不在,中国的方块字中有些也只有对称性,下列汉字是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 由5个大小相同的小正方体搭成的几何体如图所示,它的主视图是( )
4. 由5个大小相同的小正方体搭成的几何体如图所示,它的主视图是( )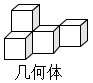 A、
A、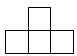 B、
B、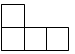 C、
C、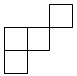 D、
D、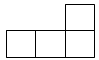 5. 已知直线 , 将一块含角的直角三角板( , )按如图方式放置,点A、B分别落在直线m、n上.若 . 则的度数为( )
5. 已知直线 , 将一块含角的直角三角板( , )按如图方式放置,点A、B分别落在直线m、n上.若 . 则的度数为( ) A、 B、 C、 D、6. 下列说法正确的是( )A、一个不透明的口袋中有3个白球和2个红球(每个球除颜色外都相同),则从中任意摸出一个球是红球的概率为 B、一个抽奖活动的中奖概率为 ,则抽奖2次就必有1次中奖 C、统计甲,乙两名同学在若干次检测中的数学成绩发现: , ,说明甲的数学成绩比乙的数学成绩稳定 D、要了解一个班有多少同学知道“杂交水稻之父”袁隆平的事迹,宜采用普查的调查方式7. 如图,四边形是的内接四边形,若 , 则的度数是( )
A、 B、 C、 D、6. 下列说法正确的是( )A、一个不透明的口袋中有3个白球和2个红球(每个球除颜色外都相同),则从中任意摸出一个球是红球的概率为 B、一个抽奖活动的中奖概率为 ,则抽奖2次就必有1次中奖 C、统计甲,乙两名同学在若干次检测中的数学成绩发现: , ,说明甲的数学成绩比乙的数学成绩稳定 D、要了解一个班有多少同学知道“杂交水稻之父”袁隆平的事迹,宜采用普查的调查方式7. 如图,四边形是的内接四边形,若 , 则的度数是( )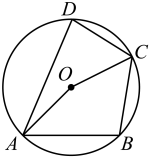 A、 B、 C、 D、8. 小明从图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:
A、 B、 C、 D、8. 小明从图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①c<0;②abc>0;③a-b+c>0;④2a-3b=0;⑤c-4b>0,
你认为其中正确信息的个数有( )
 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
9. 分解因式: .10. 式子 在实数范围内有意义,则a的取值范围是.11. 请填写一个常数,使得关于的方程有两个不相等的实数根.12. 一个不透明的袋子中装有9个小球,其中6个红球,3个绿球,这些小球除颜色外无其他差别,从袋子中随机摸出一个小球,则摸出的小球是红球的概率是;13. 小明同学逛书城,从地面一楼乘自动扶梯,随扶梯移动了13米,到达距离地面5米高的二楼,则该自动扶梯的坡度 .14. 如图放置的 , , , …都是边长为2的等边三角形,边在y轴上点 , , , …都在直线上,则点的坐标是 .

三、解答题
-
15. 计算:16. 已知关于x的一元二次方程 .(1)、求证:不论m取何值,该方程都有两个不相等的实数根;(2)、设方程的两个根分别为 , 且 , 若 , 求m的值.17. 已知:如图,点A、D、C、F在同一直线上, , , .
求证: .
 18. 某校数学兴趣小组利用无人机测量烈士塔的高度.无人机在点A处测得烈士塔顶部点B的仰角为 , 烈士塔底部点C的俯角为 , 无人机与烈士塔的水平距离为10m,求烈士塔的高度.(结果保留整数.参考数据: , , )
18. 某校数学兴趣小组利用无人机测量烈士塔的高度.无人机在点A处测得烈士塔顶部点B的仰角为 , 烈士塔底部点C的俯角为 , 无人机与烈士塔的水平距离为10m,求烈士塔的高度.(结果保留整数.参考数据: , , ) 19. 为改善城市人居环境,《成都市生活垃圾管理条例》(以下简称《条例》)于2021年3月1日起正式施行.某区域原来每天需要处理生活垃圾920吨,刚好被12个A型和10个B型预处置点位进行初筛、压缩等处理.已知一个A型点位比一个B型点位每天多处理7吨生活垃圾.(1)、求每个B型点位每天处理生活垃圾的吨数;(2)、由于《条例》的施行,垃圾分类要求提高,现在每个点位每天将少处理8吨生活垃圾,同时由于市民环保意识增强,该区域每天需要处理的生活垃圾比原来少10吨.若该区域计划增设A型、B型点位共5个,试问至少需要增设几个A型点位才能当日处理完所有生活垃圾?20. 如图,平面直角坐标系xOy中,▱OABC的边OC在x轴上,对角线AC,OB交于点M,函数y=(x>0)的图象经过点A(3,4)和点M.
19. 为改善城市人居环境,《成都市生活垃圾管理条例》(以下简称《条例》)于2021年3月1日起正式施行.某区域原来每天需要处理生活垃圾920吨,刚好被12个A型和10个B型预处置点位进行初筛、压缩等处理.已知一个A型点位比一个B型点位每天多处理7吨生活垃圾.(1)、求每个B型点位每天处理生活垃圾的吨数;(2)、由于《条例》的施行,垃圾分类要求提高,现在每个点位每天将少处理8吨生活垃圾,同时由于市民环保意识增强,该区域每天需要处理的生活垃圾比原来少10吨.若该区域计划增设A型、B型点位共5个,试问至少需要增设几个A型点位才能当日处理完所有生活垃圾?20. 如图,平面直角坐标系xOy中,▱OABC的边OC在x轴上,对角线AC,OB交于点M,函数y=(x>0)的图象经过点A(3,4)和点M. (1)、求k的值和点M的坐标;(2)、求▱OABC的周长.21. 为弘扬中华传统文化、某校开展“戏剧进课堂”的活动.该校随机抽取部分学生,四个类别:A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”,调查他们对戏剧的喜爱情况,将结果绘制成如图两幅不完整的统计图,根据图中提供的信息.解决下列问题:
(1)、求k的值和点M的坐标;(2)、求▱OABC的周长.21. 为弘扬中华传统文化、某校开展“戏剧进课堂”的活动.该校随机抽取部分学生,四个类别:A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”,调查他们对戏剧的喜爱情况,将结果绘制成如图两幅不完整的统计图,根据图中提供的信息.解决下列问题: (1)、此次共调查了名学生;(2)、扇形统计图中.B类所对应的扇形圆心角的大小为度;(3)、请通过计算补全条形统计图;(4)、该校共有1560名学生.估计该校表示“很喜欢”的A类的学生有多少人?22. 如图,AB是⊙O的直径,C是⊙O上一点,D是弧AC的中点,E为OD延长线上一点,且∠CAE=2∠C,AC与BD交于点H,与OE交于点F.
(1)、此次共调查了名学生;(2)、扇形统计图中.B类所对应的扇形圆心角的大小为度;(3)、请通过计算补全条形统计图;(4)、该校共有1560名学生.估计该校表示“很喜欢”的A类的学生有多少人?22. 如图,AB是⊙O的直径,C是⊙O上一点,D是弧AC的中点,E为OD延长线上一点,且∠CAE=2∠C,AC与BD交于点H,与OE交于点F. (1)、求证:AE⊥AB;(2)、求证:;(3)、若DH=9,tanC= , 求半径OA的长.23. 实践与探究(1)、操作一:如图①,将矩形纸片对折并展开,折痕与对角线交于点E,连结 , 则与的数量关系为 .
(1)、求证:AE⊥AB;(2)、求证:;(3)、若DH=9,tanC= , 求半径OA的长.23. 实践与探究(1)、操作一:如图①,将矩形纸片对折并展开,折痕与对角线交于点E,连结 , 则与的数量关系为 . (2)、操作二:如图②,摆放矩形纸片与矩形纸片 , 使B、C、G三点在一条直线上,在边上,连结 , M为的中点,连结、 . 求证: .(3)、拓展延伸:如图③,摆放正方形纸片与正方形纸片 , 使点F在边上,连结 , M为的中点,连结、、 . 已知正方形纸片的边长为5,正方形纸片的边长为 , 求 的面积.24. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B.抛物线经过点A、点B.
(2)、操作二:如图②,摆放矩形纸片与矩形纸片 , 使B、C、G三点在一条直线上,在边上,连结 , M为的中点,连结、 . 求证: .(3)、拓展延伸:如图③,摆放正方形纸片与正方形纸片 , 使点F在边上,连结 , M为的中点,连结、、 . 已知正方形纸片的边长为5,正方形纸片的边长为 , 求 的面积.24. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B.抛物线经过点A、点B. (1)、求抛物线的函数表达式并直接写出顶点的坐标;(2)、若在第三象限的抛物线上有一动点M,当点M到直线AB的距离最大时,求点M的坐标;(3)、点C,D分别为线段AO,线段AB上的点,且 , 连接CD.将线段CD绕点D顺时针旋转90度,点C旋转后的对应点为点E,连接OE.当线段OE的长最小时,请直接写出直线DE的函数表达式 .
(1)、求抛物线的函数表达式并直接写出顶点的坐标;(2)、若在第三象限的抛物线上有一动点M,当点M到直线AB的距离最大时,求点M的坐标;(3)、点C,D分别为线段AO,线段AB上的点,且 , 连接CD.将线段CD绕点D顺时针旋转90度,点C旋转后的对应点为点E,连接OE.当线段OE的长最小时,请直接写出直线DE的函数表达式 .