江西2023年最新中考模拟训练数学三
试卷更新日期:2023-04-18 类型:中考模拟
一、单选题
-
1. 下列各数中,是无理数的是( )A、 B、0 C、1 D、2. 计算的结果为( )A、 B、 C、 D、3. 将一个小正方体按图中所示的方式展开,则在展开图中表示棱a的线段可以是( )
 A、线段 B、线段 C、线段 D、线段4. “双减”政策实施后,中小学生的家庭作业明显减少.下图是某班甲、乙两名同学一周内每天完成家庭作业所花费时间的折线统计图,则下列说法正确的是( )
A、线段 B、线段 C、线段 D、线段4. “双减”政策实施后,中小学生的家庭作业明显减少.下图是某班甲、乙两名同学一周内每天完成家庭作业所花费时间的折线统计图,则下列说法正确的是( ) A、从星期三到星期六,甲每天完成家庭作业所花费的时间逐天减少 B、同一天中,甲、乙两人完成家庭作业所花费的时间最短相差0.5h C、这周甲平均每天完成家庭作业所花费的时间比乙长 D、这周甲完成家庭作业所花费的时间比乙稳定5. 如图,从A点发出的光线 , 经平面镜反射后得到反射光线 , , m,n为法线,设 , , , 那么之间的数量关系是( )
A、从星期三到星期六,甲每天完成家庭作业所花费的时间逐天减少 B、同一天中,甲、乙两人完成家庭作业所花费的时间最短相差0.5h C、这周甲平均每天完成家庭作业所花费的时间比乙长 D、这周甲完成家庭作业所花费的时间比乙稳定5. 如图,从A点发出的光线 , 经平面镜反射后得到反射光线 , , m,n为法线,设 , , , 那么之间的数量关系是( )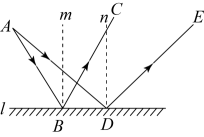 A、 B、 C、 D、6. 如图,抛物线与抛物线相交于A,B两点,顶点分别为M,N,则下列说法错误的是( )
A、 B、 C、 D、6. 如图,抛物线与抛物线相交于A,B两点,顶点分别为M,N,则下列说法错误的是( ) A、当或时, B、当时, C、当时,同时随着x的增大而增大 D、四边形是平行四边形
A、当或时, B、当时, C、当时,同时随着x的增大而增大 D、四边形是平行四边形二、填空题
-
7. 若式子有意义,则x的取值范围为 .8. 2022年10月16日上午10时,中国共产党第二十次全国代表大会在北京人民大会堂开幕,二十大代表共有2296名,这些代表是从全国9600多万党员中选举产生的.将9600万用科学记数法表示为 .9. 杨辉,字谦光,南宋时期杭州人,在他1261年所著的《详解九章算法》一书中,辑录了如下图所示的三角形数表,称之为“开方作法本源图”,还说明此表引自11世纪中叶(约公元1050年)贾宪的《释锁算术》,并绘画了“古法七乘方图”,故此,杨辉三角又被称为“贾宪三角”.探索杨辉三角中每一行的所有数字之和的规律,可求出第7行中所有数字之和为 .
 10. 已知m,n是一元二次方程的两个根,则多项式的值为 .11. 如图,在四边形ABCD中, , , , 若线段AC关于直线AB,AD对称的图形分别为线段 , 线段 , 点在直线BD上,则AC的长为 .
10. 已知m,n是一元二次方程的两个根,则多项式的值为 .11. 如图,在四边形ABCD中, , , , 若线段AC关于直线AB,AD对称的图形分别为线段 , 线段 , 点在直线BD上,则AC的长为 . 12. 如图,在菱形中,对角线 , 相交于点O, , , E为的中点,F为线段上一动点,当为等腰三角形时,的长为 .
12. 如图,在菱形中,对角线 , 相交于点O, , , E为的中点,F为线段上一动点,当为等腰三角形时,的长为 .
三、解答题
-
13.(1)、化简:(2)、解不等式组:14. 近年来,妇女权益得到有力保障,参加养老保险(即城镇职工养老保险和城乡居民养老保险)的妇女人数越来越多,2022年某地区参加养老保险的妇女共有165万人,比2010年增加120万人,其中参加城镇职工养老保险和城乡居民养老保险的人数分别是2010年的1.5倍和8倍,分别求2022年参加城镇职工养老保险和城乡居民养老保险的妇女人数.15. 某银行柜台在储户人数较多时常开放1、2、3号窗口办理日常业务,一般是先到取号机拿号按顾客“先到达,先服务”的方式服务.(1)、储户在1号窗口办业务的概率是 .(2)、储户乙取号时发现储户甲已办理完业务准备离开(储户甲、乙先后到达银行取号办理业务),请用画树状图或列表的方法求出储户甲、乙两人在不同窗口办理业务的概率.16. 如图,在正方形网格中,的顶点在格点上,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹).
 (1)、在图1中,作 .(2)、在图2中,作的角平分线 .17.(1)、课本再现
(1)、在图1中,作 .(2)、在图2中,作的角平分线 .17.(1)、课本再现如图1,在和中, , , ,
求证: . 我们在数学课上探索这一结论时进行了分析:要证 , 可设法证 , 若设 , 则只需证 .

请你根据以上分析,完成证明.
(2)、知识应用如图2,在四边形中, , , , 求的度数.
 18. 2022年10月12日,“天宫课堂”第三课开讲,神舟十四号乘组航天员陈冬、刘洋、蔡旭哲在中国空间站演示了A.微重力环境下毛细效应,B.水球变“懒”,C.太空趣味饮水,D.会调头的扳手四个精彩实验,被广大青少年称为“最牛网课”.为了解本次“太空科普知识”掌握情况,某校随机抽取部分学生进行问卷调查后并举行了测试,整理后得到如下统计图和统计表:
18. 2022年10月12日,“天宫课堂”第三课开讲,神舟十四号乘组航天员陈冬、刘洋、蔡旭哲在中国空间站演示了A.微重力环境下毛细效应,B.水球变“懒”,C.太空趣味饮水,D.会调头的扳手四个精彩实验,被广大青少年称为“最牛网课”.为了解本次“太空科普知识”掌握情况,某校随机抽取部分学生进行问卷调查后并举行了测试,整理后得到如下统计图和统计表:最喜欢的实验条形统计图(每人只能选一项)

“太空科普知识”测试成绩(百分制)频数统计表
组别
第1组
第2组
第3组
第4组
第5组
成绩x/分
组中值
55
65
75
85
95
频数
10
20
40
20
10
根据以上信息,回答下列问题:
(1)、这次调查的样本容量是 ▲ , 请补全条形统计图.(2)、在这次测试中,成绩的中位数在第组,成绩不低于80分的人数占测试人数的百分比为 .(3)、估计本次测试的平均数并对该校学生“太空科普知识”的掌握情况作出合理的评价(写出一条即可).19. 如图,在中, , , 在上取一点D,使 , 在上取一点E,使 , 作的外接圆 , 连接 . (1)、求证: .(2)、求证:是的切线.20. 图1是某简易座椅,图2是其侧面示意图,固定点O为椅腿和的中点,靠背的一端固定在上的点E处,将绕点E顺时针旋转180°后与重合,此时靠背收拢.已知 , , .
(1)、求证: .(2)、求证:是的切线.20. 图1是某简易座椅,图2是其侧面示意图,固定点O为椅腿和的中点,靠背的一端固定在上的点E处,将绕点E顺时针旋转180°后与重合,此时靠背收拢.已知 , , .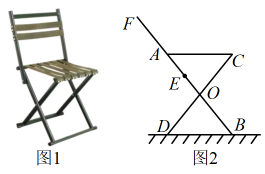 (1)、求坐垫的长.(2)、在收拢靠背的过程中,求点F到点C距离的最小值.(结果精确到;参考数据: , , , , )21. 如图,在平面直角坐标系中,一次函数(m为常数,且)的图象交x轴于点A,交y轴于点B,点C在x轴上,点D在反比例函数的图象上,已知四边形为矩形.
(1)、求坐垫的长.(2)、在收拢靠背的过程中,求点F到点C距离的最小值.(结果精确到;参考数据: , , , , )21. 如图,在平面直角坐标系中,一次函数(m为常数,且)的图象交x轴于点A,交y轴于点B,点C在x轴上,点D在反比例函数的图象上,已知四边形为矩形. (1)、直接写出点A,B,D的坐标(用含m的式子表示).(2)、求矩形的面积.22. 对于一个四边形给出如下定义:一组对角为 , 一组邻边相等的四边形称为“六零”四边形.(1)、图1是一个“六零”四边形,其中 , .
(1)、直接写出点A,B,D的坐标(用含m的式子表示).(2)、求矩形的面积.22. 对于一个四边形给出如下定义:一组对角为 , 一组邻边相等的四边形称为“六零”四边形.(1)、图1是一个“六零”四边形,其中 , .
①猜想与的数量关系是 ▲ ;
②证明你的猜想.
(2)、图2是一个“六零”四边形,其中 , , 连接 , .
①是三角形;
②若 , , 则(用含m,n的代数式表示).
(3)、在(2)的条件下,如图3,延长到点F,使得 , 连接DF.求证: .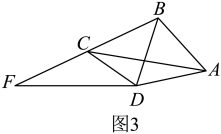 23. 已知抛物线(a,b,c是常数,)的自变量与函数值y的部分对应值如下表所示:
23. 已知抛物线(a,b,c是常数,)的自变量与函数值y的部分对应值如下表所示:…
0
1
2
…
…
5
0
0
5
…
 (1)、根据以上信息,可知抛物线开口向 , 对称轴为 .(2)、求抛物线的解析式及的值.(3)、请在下图所示的平面直角坐标系中画出所求的抛物线,设P为抛物线上的动点,过点P作直线的垂线,垂足为M,为线段PM的中点,描出相应的点 , 再把相应的点用平滑的曲线连接起来,猜想该曲线是哪种曲线(直接写出答案,不必说明理由).(4)、设直线与抛物线的两个交点记为(在左边),与(3)中的点所在曲线的两个交点记为(在左边),请根据图象直接写出线段 , 之间的数量关系: .
(1)、根据以上信息,可知抛物线开口向 , 对称轴为 .(2)、求抛物线的解析式及的值.(3)、请在下图所示的平面直角坐标系中画出所求的抛物线,设P为抛物线上的动点,过点P作直线的垂线,垂足为M,为线段PM的中点,描出相应的点 , 再把相应的点用平滑的曲线连接起来,猜想该曲线是哪种曲线(直接写出答案,不必说明理由).(4)、设直线与抛物线的两个交点记为(在左边),与(3)中的点所在曲线的两个交点记为(在左边),请根据图象直接写出线段 , 之间的数量关系: .