黑龙江省绥化市肇东市南片2023年九年级(五四制)下学期五校联考数学试题
试卷更新日期:2023-04-18 类型:中考模拟
一、单选题
-
1. 中国每年可对价值亿美元的美国进口商品征收关税.其中的亿用科学记数法表示为( )A、 B、 C、 D、2. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 一个几何体由若干个大小相同的小立方块搭成,如图是它的主视图和俯视图,该几何体最少要用a个立方块搭成,最多要用b个立方块搭成,则等于( )
3. 一个几何体由若干个大小相同的小立方块搭成,如图是它的主视图和俯视图,该几何体最少要用a个立方块搭成,最多要用b个立方块搭成,则等于( ) A、 B、 C、 D、4. 函数中,自变量的取值范围是( )A、且 B、 C、 D、5. 规定一种新运算“※”,如果a,b是有理数,那么 , 则等于( )A、3 B、6 C、2 D、06. 下列命题是真命题的是( )A、的两边为3,4,则斜边上的高是 B、角是轴对称图形,它的平分线所在的直线就是它的对称轴 C、三角形三个内角平分线的交点到三个顶点的距离相等 D、对角线互相垂直平分的四边形是正方形7. 下列运算正确的是( )A、 B、 C、 D、8. 如图,在中, , , , 点P从点A出发沿的路径运动到点C停止,点Q以相同的速度沿的路径运动到点C停止,连接 , 设点P的运动路程为x,的面积为y,则下列图象能大致反映y与x之间的函数关系的是( )
A、 B、 C、 D、4. 函数中,自变量的取值范围是( )A、且 B、 C、 D、5. 规定一种新运算“※”,如果a,b是有理数,那么 , 则等于( )A、3 B、6 C、2 D、06. 下列命题是真命题的是( )A、的两边为3,4,则斜边上的高是 B、角是轴对称图形,它的平分线所在的直线就是它的对称轴 C、三角形三个内角平分线的交点到三个顶点的距离相等 D、对角线互相垂直平分的四边形是正方形7. 下列运算正确的是( )A、 B、 C、 D、8. 如图,在中, , , , 点P从点A出发沿的路径运动到点C停止,点Q以相同的速度沿的路径运动到点C停止,连接 , 设点P的运动路程为x,的面积为y,则下列图象能大致反映y与x之间的函数关系的是( )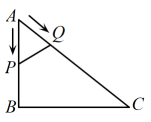 A、
A、 B、
B、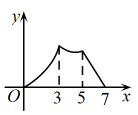 C、
C、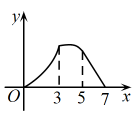 D、
D、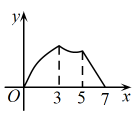 9. 爱心文具店购进A,B两种款式的圆珠笔,其中A种圆珠笔的单价比B种圆珠笔的单价低 . 已知购进A种圆珠笔用了元,购进B种圆珠笔用了元,且所购进的A种圆珠笔的数量比B种圆珠笔多盒.设文具店购进B种款式的圆珠笔x盒,则所列方程正确的是( )A、 B、 C、 D、10. 已知不等式组至少有两个整数解,则a的取值范围是( )A、 B、 C、 D、11. 如图,为的直径,且 , C为的中点,四边形为平行四边形,是的切线,则图中阴影部分的面积为( )
9. 爱心文具店购进A,B两种款式的圆珠笔,其中A种圆珠笔的单价比B种圆珠笔的单价低 . 已知购进A种圆珠笔用了元,购进B种圆珠笔用了元,且所购进的A种圆珠笔的数量比B种圆珠笔多盒.设文具店购进B种款式的圆珠笔x盒,则所列方程正确的是( )A、 B、 C、 D、10. 已知不等式组至少有两个整数解,则a的取值范围是( )A、 B、 C、 D、11. 如图,为的直径,且 , C为的中点,四边形为平行四边形,是的切线,则图中阴影部分的面积为( ) A、 B、 C、 D、12. 如图,在正方形中,E是线段上一动点,连接交于点F,过点F作交于点G,连接 , 现有以下结论:①是等腰直角三角形;②;③点A到的距离等于正方形的边长;④当点E运动到的三等分点时,或 . 以上结论正确的个数有( )
A、 B、 C、 D、12. 如图,在正方形中,E是线段上一动点,连接交于点F,过点F作交于点G,连接 , 现有以下结论:①是等腰直角三角形;②;③点A到的距离等于正方形的边长;④当点E运动到的三等分点时,或 . 以上结论正确的个数有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 某冷库的温度是 , 下降了 , 则变化后的冷库的温度是 .14. 若式子在实数范围内有意义,则x的取值范围是 .15. 因式分解: =16. 若一组数据1, ,3的平均数为 ,则这组数据的方差是.17. 化简: .18. 若圆锥的底面直径为6cm,母线长为10cm,则圆锥的侧面积为cm2 .19. 如图,轮船B在码头A的正东方向,与码头A的距离为100海里,轮船B向北航行40海里到达C处时,接到D处一艘渔船发来的求救信号,于是沿北偏西45°方向航行到D处,解教渔船后轮船沿南偏西82°返回到码头A,那么码头A与D的距离为海里.(结果保留整数,参考数据: , , . )
 20. 甲计划用若干个工作日完成某项工作,从第三个工作日起,乙加入此项工作,且甲乙两人工效率相同,结果提前天完成任务,则甲计划完成此项工作的天数是 .21. 菱形中, , 以为边长作正方形 , 连接 , 则的度数为 .22. 如图,点 , 点 , 点 , 点 , 按照这样的规律下去,点的坐标为 .
20. 甲计划用若干个工作日完成某项工作,从第三个工作日起,乙加入此项工作,且甲乙两人工效率相同,结果提前天完成任务,则甲计划完成此项工作的天数是 .21. 菱形中, , 以为边长作正方形 , 连接 , 则的度数为 .22. 如图,点 , 点 , 点 , 点 , 按照这样的规律下去,点的坐标为 .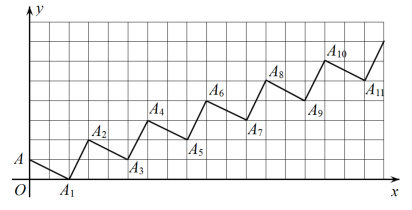
三、解答题
-
23. 已知 , , , .
 (1)、试用直尺和圆规作的中垂线.(不写作法,保留痕迹)(2)、的中垂线交于点 , 求的面积.24. 关于的一元二次方程有实数根.求:(1)、求的范围;(2)、设为方程的两个根,且 , 求的值?25. 如图,已知一次函数和反比例函数的图象交于点 , , 求:
(1)、试用直尺和圆规作的中垂线.(不写作法,保留痕迹)(2)、的中垂线交于点 , 求的面积.24. 关于的一元二次方程有实数根.求:(1)、求的范围;(2)、设为方程的两个根,且 , 求的值?25. 如图,已知一次函数和反比例函数的图象交于点 , , 求: (1)、求一次函数及反比例函数的解析式;(2)、在轴取一点 , 当的面积为6时,求的坐标?(3)、当取何值时,?
(1)、求一次函数及反比例函数的解析式;(2)、在轴取一点 , 当的面积为6时,求的坐标?(3)、当取何值时,?


