河北省石家庄市长安区2023年初中毕业生基础知识质量检测数学试卷
试卷更新日期:2023-04-18 类型:中考模拟
一、单选题
-
1. 将一张四边形纸片沿直线剪开,剪开后的两个图形内角和相等的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若成立,则“”中的运算符号是( )A、 B、 C、 D、3. 图中的两个三角板是位似图形,则位似中心可能是( )
2. 若成立,则“”中的运算符号是( )A、 B、 C、 D、3. 图中的两个三角板是位似图形,则位似中心可能是( ) A、点A B、点 C、点 D、点4. 与相等的是( )A、 B、 C、 D、5. 如图,烧杯内液体表面与烧杯下底部平行,光线从液体中射向空气时发生折射,光线变成 , 点在射线上.已知 , , 则( )
A、点A B、点 C、点 D、点4. 与相等的是( )A、 B、 C、 D、5. 如图,烧杯内液体表面与烧杯下底部平行,光线从液体中射向空气时发生折射,光线变成 , 点在射线上.已知 , , 则( ) A、 B、 C、 D、6. 如图,若 , 则表示的值的点落在( )
A、 B、 C、 D、6. 如图,若 , 则表示的值的点落在( ) A、第①段 B、第②段 C、第③段 D、第④段7. 甲、乙两人一起玩如图4的转盘游戏,将两个转盘各转一次,指针指向的数的和为正数,甲胜,否则乙胜,这个游戏( )
A、第①段 B、第②段 C、第③段 D、第④段7. 甲、乙两人一起玩如图4的转盘游戏,将两个转盘各转一次,指针指向的数的和为正数,甲胜,否则乙胜,这个游戏( ) A、公平 B、对甲有利 C、对乙有利 D、公平性不可预测8. 下图是由9个同样大小的小正方体组成的几何体.将小正方体①移到②的正上方后,关于新几何体的三视图描述正确的是( )
A、公平 B、对甲有利 C、对乙有利 D、公平性不可预测8. 下图是由9个同样大小的小正方体组成的几何体.将小正方体①移到②的正上方后,关于新几何体的三视图描述正确的是( )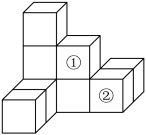 A、主视图和俯视图改变 B、俯视图和左视图改变 C、左视图和俯视图不变 D、俯视图和主视图不变9. 如图,在边长为的正方形纸片中剪下一个边长为的正方形,剩余部分(即阴影部分)可剪拼成一个长方形,若拼成的长方形一边长为 , 则另一边长为( )
A、主视图和俯视图改变 B、俯视图和左视图改变 C、左视图和俯视图不变 D、俯视图和主视图不变9. 如图,在边长为的正方形纸片中剪下一个边长为的正方形,剩余部分(即阴影部分)可剪拼成一个长方形,若拼成的长方形一边长为 , 则另一边长为( )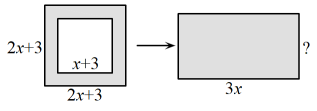 A、 B、 C、 D、10. 如图,中, , 点在的延长线上,且 , 则( )
A、 B、 C、 D、10. 如图,中, , 点在的延长线上,且 , 则( ) A、 B、 C、 D、11. 如图,将折叠,使边落在边上,展开后得到折痕 . 将再次折叠,使边落在边上,展开后得到折痕 , , 交于点 . 则以下结论一定成立的是( )
A、 B、 C、 D、11. 如图,将折叠,使边落在边上,展开后得到折痕 . 将再次折叠,使边落在边上,展开后得到折痕 , , 交于点 . 则以下结论一定成立的是( )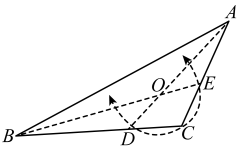 A、 B、 C、点到三边的距离相等 D、点到三个顶点的距离相等12. 《孙子算经》中有一道题,原文是:今有三人共车,二车空:二人共车,九人步,问人与车各几何?译文为:今有若干人乘车,每3人共乘一车,最终剩余2辆车;若每2人共乘一车,最终剩余9个人无车可乘,问共有多少辆车?设共有x辆车,则( )A、 B、 C、 D、13. 阅读下面的材料:
A、 B、 C、点到三边的距离相等 D、点到三个顶点的距离相等12. 《孙子算经》中有一道题,原文是:今有三人共车,二车空:二人共车,九人步,问人与车各几何?译文为:今有若干人乘车,每3人共乘一车,最终剩余2辆车;若每2人共乘一车,最终剩余9个人无车可乘,问共有多少辆车?设共有x辆车,则( )A、 B、 C、 D、13. 阅读下面的材料:定理:三角形的中位线平行于第三边,并且等于第三边的一半.
已知:如图,在中, , 分别是边 , 的中点.
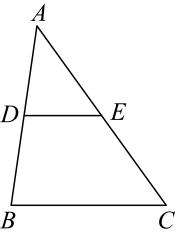
求证: , 且 .
证明:延长到点 , 使 , 连接 , …
甲、乙两人后续证明的部分思路如下:
甲:如图1,先证明 , 再推理得出四边形是平行四边形.
乙:如图2,连接 , . 先后证明四边形 , 分别是平行四边形.
下列判断正确的是( )
 A、甲思路正确,乙思路不符合题意 B、甲思路错误,乙思路正确 C、甲、乙两人思路都正确 D、甲、乙两人思路都错误14. 观察下面的尺规作图痕迹,在平行四边形基础上能成功作出菱形的是( )
A、甲思路正确,乙思路不符合题意 B、甲思路错误,乙思路正确 C、甲、乙两人思路都正确 D、甲、乙两人思路都错误14. 观察下面的尺规作图痕迹,在平行四边形基础上能成功作出菱形的是( ) A、①②③ B、①② C、①③ D、②③15. 如图,在 中, , , .动点 沿 从点 向点 移动,过点 作 的垂线,交折线 于点 .记 , 的面积为 ,则 关于 的函数图象大致是( )
A、①②③ B、①② C、①③ D、②③15. 如图,在 中, , , .动点 沿 从点 向点 移动,过点 作 的垂线,交折线 于点 .记 , 的面积为 ,则 关于 的函数图象大致是( )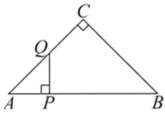 A、
A、 B、
B、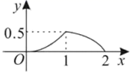 C、
C、 D、
D、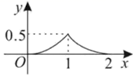 16. 如图,点是边长为2的正六边形内的一点(不包括边界),且 , 是上的一点,是的中点,则的最小值为( )
16. 如图,点是边长为2的正六边形内的一点(不包括边界),且 , 是上的一点,是的中点,则的最小值为( ) A、 B、 C、3 D、2
A、 B、 C、3 D、2二、填空题
-
17. 如图,故宫又称紫禁城,位于北京中轴线的中心,占地面积约 , 在世界宫殿建筑群中面积最大.将720000用科学记数法表示为 .
 18. 如图1,冰激凌的外壳(不计厚度)可近似的看作圆锥,其母线长为 , 底面圆直径长为 .
18. 如图1,冰激凌的外壳(不计厚度)可近似的看作圆锥,其母线长为 , 底面圆直径长为 . (1)、这个冰激凌外壳的侧面展开图的形状是;(2)、当冰激凌被吃掉一部分后,其外壳仍可近似的看作圆锥,如图2,其母线长为 , 则此时冰激凌外壳的侧面积为 . (结果保留)19. 将等腰直角三角形按图的方式放在平面直角坐标系中,其中点 , 点 , 点在双曲线的图象上.
(1)、这个冰激凌外壳的侧面展开图的形状是;(2)、当冰激凌被吃掉一部分后,其外壳仍可近似的看作圆锥,如图2,其母线长为 , 则此时冰激凌外壳的侧面积为 . (结果保留)19. 将等腰直角三角形按图的方式放在平面直角坐标系中,其中点 , 点 , 点在双曲线的图象上.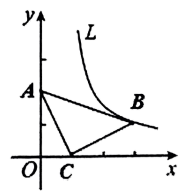 (1)、;(2)、将沿着轴正方向平移个单位得到 .
(1)、;(2)、将沿着轴正方向平移个单位得到 .①当双曲线过线段的中点时,点的坐标是;
②当线段和双曲线有公共点时,的取值范围是 .
三、解答题
-
20. 如图是一道关于整式运算的例题及正确的解答过程,其中是两个关于的二项式.
 (1)、直接写出二项式和 , 并求出该题目的最后运算结果;(2)、若 , 求的最小整数值.21. 某中学为了解学生对“航空航天知识”的掌握情况,随机抽取50名学生进行测试,并对成绩(满分100分)进行分组整理,各小组的成绩(分)分段为: , , , , , 信息如下:
(1)、直接写出二项式和 , 并求出该题目的最后运算结果;(2)、若 , 求的最小整数值.21. 某中学为了解学生对“航空航天知识”的掌握情况,随机抽取50名学生进行测试,并对成绩(满分100分)进行分组整理,各小组的成绩(分)分段为: , , , , , 信息如下:a.成绩频数分布图如图所示:
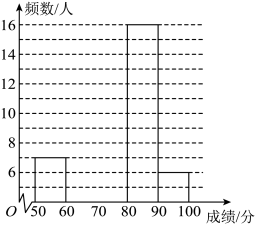
b.成绩在这一组的是(单位:分):
70 71 72 72 74 77 78 78 78 79 79 79
根据以上信息,回答下列问题:
(1)、补全统计图并求成绩不低于80分的人数占测试人数的百分比;(2)、求这次测试成绩的中位数;(3)、这次测试成绩的平均数是76.4分,甲的测试成绩是77分.乙说:“甲的成绩高于平均数,所以甲的成绩高于一半学生的成绩.”你认为乙的说法符合题意吗?请说明理由.22. 发现:一个两位数的平方与其个位数字的平方的差,一定是的倍数.如: , 是的倍; , 是的倍.(1)、请你仿照上面的例子,再举出一个例子:;(2)、十位数字为1,个位数字为的两位数可表示为 , 若该两位数的平方与的平方的差是的倍,则;(3)、设一个两位数的十位数字为 , 个位数字为( , , 且 , 为正整数),请用含 , 的式子论证“发现”的结论是否符合题意.23. 服装厂有甲、乙两条生产线,生产一款由上衣和裤子配套的运动套装,甲生产线专门生产套装的上衣,乙生产线专门生产套装的裤子.某天两条生产线同时开始生产,乙生产线在生产中停产一段时间更换了新设备,更换新设备后,生产效率是更换前的2倍.甲、乙生产线各自生产的服装数量(件)与生产时间(小时)的函数关系如图所示.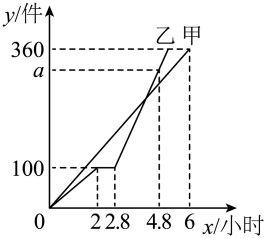 (1)、求甲生产线生产的套装上衣(件)与工作时间(小时)的函数关系式;(2)、求图中的值;(3)、乙生产线使用更换的新设备后,在生产过程中,甲、乙两条生产线每小时的损耗成本分别是30元和80元,若生产一批上衣和裤子成套的运动套装的总损耗成本不超过520元,则这批运动套装最多是多少套?24. 如图,在中, , 平分并交于点 , 点在上,经过点 , 的半圆分别交 , 于点 , , 连接 .
(1)、求甲生产线生产的套装上衣(件)与工作时间(小时)的函数关系式;(2)、求图中的值;(3)、乙生产线使用更换的新设备后,在生产过程中,甲、乙两条生产线每小时的损耗成本分别是30元和80元,若生产一批上衣和裤子成套的运动套装的总损耗成本不超过520元,则这批运动套装最多是多少套?24. 如图,在中, , 平分并交于点 , 点在上,经过点 , 的半圆分别交 , 于点 , , 连接 . (1)、求证:是的切线;(2)、判断和的数量关系,并说明理由;(3)、若的半径为5, , 求点到直线的距离.25. 如图,直线与轴交于点 , 与轴交于点 , 抛物线(为常数).
(1)、求证:是的切线;(2)、判断和的数量关系,并说明理由;(3)、若的半径为5, , 求点到直线的距离.25. 如图,直线与轴交于点 , 与轴交于点 , 抛物线(为常数).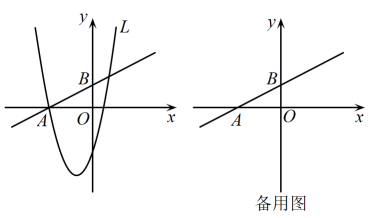 (1)、当经过点时,求的表达式及顶点坐标;(2)、当经过坐标原点时,设与轴的另一个交点为点 . 上是否存在点 , 使的面积是面积的2倍?若存在,求出此时点的坐标,若不存在,说明理由;(3)、若与线段只有一个交点,直接写出的取值范围.26. 如图1,正方形与正方形有公共点 , 点 , 分别在 , 上,点在正方形的对角线上.将正方形绕点逆时针方向旋转,旋转角为().
(1)、当经过点时,求的表达式及顶点坐标;(2)、当经过坐标原点时,设与轴的另一个交点为点 . 上是否存在点 , 使的面积是面积的2倍?若存在,求出此时点的坐标,若不存在,说明理由;(3)、若与线段只有一个交点,直接写出的取值范围.26. 如图1,正方形与正方形有公共点 , 点 , 分别在 , 上,点在正方形的对角线上.将正方形绕点逆时针方向旋转,旋转角为(). (1)、当时,;(2)、如图2,当时,连接 , , 是否为定值?请说明理由;(3)、若 , , 当 , , 三点共线时,求的长度.
(1)、当时,;(2)、如图2,当时,连接 , , 是否为定值?请说明理由;(3)、若 , , 当 , , 三点共线时,求的长度.