广东省广州市天河区2023年中考一模数学试卷
试卷更新日期:2023-04-18 类型:中考模拟
一、单选题
-
1. 如图是某几何体的展开图,该几何体是( )
 A、长方体 B、圆柱 C、圆锥 D、三棱柱2. 下列图案中,是中心对称图形的是( )A、
A、长方体 B、圆柱 C、圆锥 D、三棱柱2. 下列图案中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 分式方程的解是( )A、 B、 C、 D、4. 点在一次函数的图象上,则的值为( )A、13 B、1 C、5 D、5. 下列各式计算正确的是( ).A、 B、 C、 D、6. 实数 , 在数轴上的对应点的位置如图所示,下列结论中正确的是( )
3. 分式方程的解是( )A、 B、 C、 D、4. 点在一次函数的图象上,则的值为( )A、13 B、1 C、5 D、5. 下列各式计算正确的是( ).A、 B、 C、 D、6. 实数 , 在数轴上的对应点的位置如图所示,下列结论中正确的是( ) A、 B、 C、 D、7. 二次函数的图象可能是( )A、
A、 B、 C、 D、7. 二次函数的图象可能是( )A、 B、
B、 C、
C、 D、
D、 8. 不透明的袋子中装有两个小球,上面分别写着“0”,“1”,除数字外两个小球无其他差别,从中随机摸出一个小球,记录其数字,放回并摇匀,再从中随机摸出一个小球,记录其数字,那么两次记录的数字之积为0的概率是( )A、 B、 C、 D、9. 按如图所示的规律搭正方形:搭一个小正方形需要4根小棒,搭两个小正方形需要7根小棒,则搭2023个这样的小正方形需要小棒( )
8. 不透明的袋子中装有两个小球,上面分别写着“0”,“1”,除数字外两个小球无其他差别,从中随机摸出一个小球,记录其数字,放回并摇匀,再从中随机摸出一个小球,记录其数字,那么两次记录的数字之积为0的概率是( )A、 B、 C、 D、9. 按如图所示的规律搭正方形:搭一个小正方形需要4根小棒,搭两个小正方形需要7根小棒,则搭2023个这样的小正方形需要小棒( ) A、6068根 B、6069根 C、6070根 D、6071根10. 如图,在正方形中,点在边上,且 , 连接 , , 平分 , 过点作于点 , 若正方形的边长为4,则的面积是( )
A、6068根 B、6069根 C、6070根 D、6071根10. 如图,在正方形中,点在边上,且 , 连接 , , 平分 , 过点作于点 , 若正方形的边长为4,则的面积是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. -2023的绝对值是 .12. 若x=1是方程x2-3x+a=0的解,则a的值为 .13. 分解因式: = .14. 如图,是的直径, , 交于点 , 连接 , 若 , 则的度数为 .
 15. 如图,在中, , , 为的中点,分别与 , 相切于 , 两点,则的半径长为 .
15. 如图,在中, , , 为的中点,分别与 , 相切于 , 两点,则的半径长为 . 16. 如图,中, , 点在上,且 , 为上任意一点,若将绕A点逆时针旋转90°得到 , 连接 , 则在点运动过程中,线段的最小值为 .
16. 如图,中, , 点在上,且 , 为上任意一点,若将绕A点逆时针旋转90°得到 , 连接 , 则在点运动过程中,线段的最小值为 .
三、解答题
-
17. 解不等式:18. 如图,点A、F、C、D在同一直线上,点B和点E分别位于直线的两侧,且 . 求证: .
 19. 某校共有1000名学生,准备成立四个球类活动小组:A篮球,B足球,C排球,D羽毛球,为了解学生对四个活动小组的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中必须选择而且只能选择一个小组,根据调查结果绘制如下两幅不完整的统计图.
19. 某校共有1000名学生,准备成立四个球类活动小组:A篮球,B足球,C排球,D羽毛球,为了解学生对四个活动小组的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中必须选择而且只能选择一个小组,根据调查结果绘制如下两幅不完整的统计图.
请结合图中所给信息,解答下列问题:
(1)、填空:本次调査中,抽査的学生总数是;扇形统计图中的值是;(2)、补全条形统计图,并估计该校学生喜爱羽毛球的学生人数.20. 一辆客车从A地出发前往地,平均速度(千米小时)与所用时间(小时)的函数关系如图所示,其中 . (1)、求与的函数关系式及的取值范围;(2)、客车上午8点从A地出发,客车需在当天14点至15点30分(含14点与15点30分)间到达地,求客车行驶速度的取值范围.21. 已知代数式 .(1)、化简;(2)、若一个矩形两条对角线的长为的两根,求的值.22. 如图,在中, , 以为直径的与交于点 , 连接 .
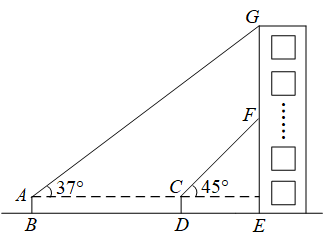
(1)、求与的函数关系式及的取值范围;(2)、客车上午8点从A地出发,客车需在当天14点至15点30分(含14点与15点30分)间到达地,求客车行驶速度的取值范围.21. 已知代数式 .(1)、化简;(2)、若一个矩形两条对角线的长为的两根,求的值.22. 如图,在中, , 以为直径的与交于点 , 连接 . (1)、尺规作图:作劣弧的中点;(不写作法,保留作图痕迹)(2)、若与相切,求(1)中作图得到的的度数.23. 北京时间2022年4月16日9时56分,神舟十三号载人飞船返回舱成功着陆.为弘扬航天精神,某校在教学楼上悬挂了一幅长为的励志条幅(即).小亮同学想知道条幅的底端到地面的距离,他的测量过程如下:如图,首先他站在楼前点处,在点正上方点处测得条幅顶端的仰角为 , 然后向教学楼条幅方向前行到达点处(楼底部点与点 , 在一条直线上),在点正上方点处测得条幅底端的仰角为 , 若 , 均为(即四边形为矩形),请你帮助小亮计算条幅底端到地面的距离的长度.(结果精确到 , 参考数据: , , )
(1)、尺规作图:作劣弧的中点;(不写作法,保留作图痕迹)(2)、若与相切,求(1)中作图得到的的度数.23. 北京时间2022年4月16日9时56分,神舟十三号载人飞船返回舱成功着陆.为弘扬航天精神,某校在教学楼上悬挂了一幅长为的励志条幅(即).小亮同学想知道条幅的底端到地面的距离,他的测量过程如下:如图,首先他站在楼前点处,在点正上方点处测得条幅顶端的仰角为 , 然后向教学楼条幅方向前行到达点处(楼底部点与点 , 在一条直线上),在点正上方点处测得条幅底端的仰角为 , 若 , 均为(即四边形为矩形),请你帮助小亮计算条幅底端到地面的距离的长度.(结果精确到 , 参考数据: , , )