广东省佛山市南海区九江镇2023年中考模拟数学试卷
试卷更新日期:2023-04-18 类型:中考模拟
一、单选题
-
1. 抛物线的对称轴是( )A、直线 B、直线 C、直线 D、直线2. 以下几何体的主视图与左视图不一定相同的是( )A、
 B、
B、 C、
C、 D、
D、 3. 已知是方程的根,则代数式的值为( )A、4044 B、 C、2024 D、4. “二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明”.若要从“立春”“立夏”“秋分”“大寒”四张邮票中抽取两张,则恰好抽到“立夏”、“秋分”两张邮票的概率是( )A、 B、 C、 D、5. 如图,四边形是的内接四边形,点是的中点,点是上的一点,若 , 则的度数是( )
3. 已知是方程的根,则代数式的值为( )A、4044 B、 C、2024 D、4. “二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明”.若要从“立春”“立夏”“秋分”“大寒”四张邮票中抽取两张,则恰好抽到“立夏”、“秋分”两张邮票的概率是( )A、 B、 C、 D、5. 如图,四边形是的内接四边形,点是的中点,点是上的一点,若 , 则的度数是( ) A、 B、 C、 D、6. “读万卷书,行万里路”某校为了丰富学生的阅历知识,坚持开展课外阅读活动,学生人均阅读量从七年级的每年100万字增加到九年级的每年144万字.设该校七至九年级人均阅读量年均增长率为 , 则可列方程为( )A、 B、 C、 D、7. 已知反比例函数图象过点 , 若 , 则的取值范围是( )A、 B、 C、或 D、或8. 大约在两千四五百年前,墨子和他的学生做了世界上第1个小孔成倒像的实验.并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图所示的小孔成像实验中,若物距为 , 像距为 , 蜡烛火焰倒立的像的高度是 , 则蜡烛火焰的高度是( )
A、 B、 C、 D、6. “读万卷书,行万里路”某校为了丰富学生的阅历知识,坚持开展课外阅读活动,学生人均阅读量从七年级的每年100万字增加到九年级的每年144万字.设该校七至九年级人均阅读量年均增长率为 , 则可列方程为( )A、 B、 C、 D、7. 已知反比例函数图象过点 , 若 , 则的取值范围是( )A、 B、 C、或 D、或8. 大约在两千四五百年前,墨子和他的学生做了世界上第1个小孔成倒像的实验.并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图所示的小孔成像实验中,若物距为 , 像距为 , 蜡烛火焰倒立的像的高度是 , 则蜡烛火焰的高度是( ) A、 B、6 C、 D、89. 如图,在平面直角坐标系中,点分别在轴负半轴和轴正半轴上,点在上, , 连接 , 过点作交的延长线于 . 若 , 则的值是( )
A、 B、6 C、 D、89. 如图,在平面直角坐标系中,点分别在轴负半轴和轴正半轴上,点在上, , 连接 , 过点作交的延长线于 . 若 , 则的值是( )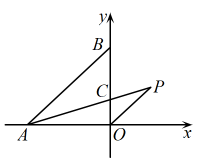 A、 B、3 C、 D、210. 已知抛物线上部分点的横坐标 , 纵坐标的对应值如表所示,为常数:
A、 B、3 C、 D、210. 已知抛物线上部分点的横坐标 , 纵坐标的对应值如表所示,为常数:…
0
1
…
…
2
6
…
给出下列说法:①抛物线开口向上;②抛物线顶点坐标为;③抛物线与轴交点为;④抛物线与轴有两个交点;⑤抛物线对称轴在轴右侧;以上说法正确的是( )
A、①②③ B、②③④ C、③④⑤ D、②④⑤二、填空题
-
11. 一个多边形的外角和是内角和的一半,则这个多边形的边数为 .12. 请找一个实数 , 使得关于的方程有两个不相等的实数根,则 .13. 如图,圆锥的高 , 底面圆直径 , 则圆锥的表面积为 .
 14. 如图,把矩形纸片放入平面直角坐标系中,使分别落在x轴、y轴上,连接 , 将纸片沿折叠,使点B落在点D的位置,与y轴交于点E,若 , 则点E的坐标为 .
14. 如图,把矩形纸片放入平面直角坐标系中,使分别落在x轴、y轴上,连接 , 将纸片沿折叠,使点B落在点D的位置,与y轴交于点E,若 , 则点E的坐标为 . 15. 在平面直角坐标系中,直线经过点 . 将点向右平移到轴上,得到点 , 设点关于原点的对称点为 , 记线段与组成的图形为 . 若双曲线与图形恰有一个公共点,结合函数图象,则的取值范围为 .
15. 在平面直角坐标系中,直线经过点 . 将点向右平移到轴上,得到点 , 设点关于原点的对称点为 , 记线段与组成的图形为 . 若双曲线与图形恰有一个公共点,结合函数图象,则的取值范围为 .三、解答题
-
16. 计算:17. 如图,在中, .
 (1)、尺规作图:作 , 使它过点 , 且圆心在上,(必须保留清晰的作图痕迹,不写作法);(2)、在(1)所作的中,求证:点在上.18. 如图是一个正方体的展开图,已知它折叠成正方体后相对两个面上的数字之和相等.若从正方体展开图中这六个数中随机选出两个数分别作为一元二次方程中系数的值,请列表法或树状图法求这个一元二次方程没有实数根的概率.
(1)、尺规作图:作 , 使它过点 , 且圆心在上,(必须保留清晰的作图痕迹,不写作法);(2)、在(1)所作的中,求证:点在上.18. 如图是一个正方体的展开图,已知它折叠成正方体后相对两个面上的数字之和相等.若从正方体展开图中这六个数中随机选出两个数分别作为一元二次方程中系数的值,请列表法或树状图法求这个一元二次方程没有实数根的概率. 19. 已知抛物线解析式(是常数).(1)、若抛物线与轴只有一个公共点,求的值;(2)、为该抛物线上一点,当取得最大值时,求点的坐标.20. 如图,在四边形 中, ,对角线 相交于点N , 点M是对角线 中点,连接 .如果 ,且 .
19. 已知抛物线解析式(是常数).(1)、若抛物线与轴只有一个公共点,求的值;(2)、为该抛物线上一点,当取得最大值时,求点的坐标.20. 如图,在四边形 中, ,对角线 相交于点N , 点M是对角线 中点,连接 .如果 ,且 . (1)、求证:四边形 是平行四边形.(2)、求 的值.21. 如图,已知一次函数图象与反比例函数的图象交于两点,其中点坐标 , 点坐标 .
(1)、求证:四边形 是平行四边形.(2)、求 的值.21. 如图,已知一次函数图象与反比例函数的图象交于两点,其中点坐标 , 点坐标 . (1)、求一次函数及反比例函数的表达式;(2)、当时,直接写出的取值范围;(3)、若点为直线上一点,当时,求点的坐标.
(1)、求一次函数及反比例函数的表达式;(2)、当时,直接写出的取值范围;(3)、若点为直线上一点,当时,求点的坐标.

