广东省东莞市2023年中考一模数学试卷
试卷更新日期:2023-04-18 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、2 B、 C、 D、2. 下列四个图形中,既是中心对称图形,又是轴对称图形的是( )A、
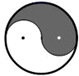 B、
B、 C、
C、 D、
D、 3. 国家统计局发布2021年国内生产总值达到1140000亿元,比上年增长8.1%.将1140000用科学记数法表示应为( )A、 B、 C、 D、4. 如图是由若干个完全相同的立方体搭成的几何体,该几何体的左视图是( )
3. 国家统计局发布2021年国内生产总值达到1140000亿元,比上年增长8.1%.将1140000用科学记数法表示应为( )A、 B、 C、 D、4. 如图是由若干个完全相同的立方体搭成的几何体,该几何体的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 下列计算结果正确的是( )A、a+a2=a3 B、2a6÷a2=2a3 C、2a2•3a3=6a6 D、(2a3)2=4a66. 某校5位同学在“国学经典诵读”比赛中,成绩(单位:分)分别是86,95,97,90,88.这组数据的中位数是( )A、86 B、88 C、90 D、957. 如图所示,直线 , 则( )
5. 下列计算结果正确的是( )A、a+a2=a3 B、2a6÷a2=2a3 C、2a2•3a3=6a6 D、(2a3)2=4a66. 某校5位同学在“国学经典诵读”比赛中,成绩(单位:分)分别是86,95,97,90,88.这组数据的中位数是( )A、86 B、88 C、90 D、957. 如图所示,直线 , 则( ) A、 B、 C、 D、8. 在数轴上表示不等式组的解,其中正确的是( )A、
A、 B、 C、 D、8. 在数轴上表示不等式组的解,其中正确的是( )A、 B、
B、 C、
C、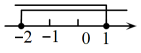 D、
D、 9. 如图,点A、B、O都在格点上,则的正切值是( )
9. 如图,点A、B、O都在格点上,则的正切值是( ) A、 B、 C、 D、10. 如图所示,正方形ABCD中,对角线AC、BD相交于点O,AE平分∠BAC ,分别交BC、BD于E、F,下列结论:①△ABF∽△ACE;②BD=AD+BE;③;④若△ABF的面积为1,则正方形ABCD的面积为 . 其中正确的结论的个数是( )
A、 B、 C、 D、10. 如图所示,正方形ABCD中,对角线AC、BD相交于点O,AE平分∠BAC ,分别交BC、BD于E、F,下列结论:①△ABF∽△ACE;②BD=AD+BE;③;④若△ABF的面积为1,则正方形ABCD的面积为 . 其中正确的结论的个数是( )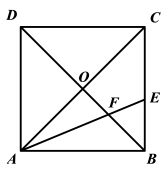 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 分解因式: .12. 已知圆锥的底面半径是 , 母线长 , 则侧面积是 .13. 在阳光下,高为6m的旗杆在地面上的影长为4m,在同一时刻,测得附近一座建筑物的影长为 , 则这座建筑物的高度为m.14. 如图,将直角三角板ABC放在平面直角坐标系中,点A,B的坐标分别为(2,1),(7,1),将三角板ABC沿x轴正方向平移,点B的对应点B'刚好落在反比例函数y=(x>0)的图象上,则点C平移的距离CC'= .
 15. 如图,是按一定规律排成的三角形数阵,按图中数阵的排列规律,第7行从左至右第3个数是 .
15. 如图,是按一定规律排成的三角形数阵,按图中数阵的排列规律,第7行从左至右第3个数是 .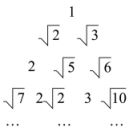
三、解答题
-
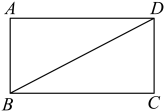
16. 计算: .17. 先化简,再求值: ,其中a= .18. 如图,是矩形的一条对角线.
 (1)、作的垂直平分线 , 分别交 , 于点E、F,垂足为点O(要求用尺规作图,保留作图痕迹.不要求写作法);(2)、若 , , 求的长.19. 我国的教育方针是:教育必须为社会主义现代化建设服务,为人民服务,与生产劳动和社会实践相结合,培养德智体美劳全面发展的社会主义建设者和接班人.为培养德智体美劳全面发展的优秀人才,丰都某中学开展了一系列精品课程,其中有一门课程《研学旅行》开展以来引起广泛关注,九年级2班数学兴趣小组对本班同学对《研学旅行》课的喜欢程度进行了调查,根据收集的数据绘制了两幅不完整的统计图,请根据图中信息,解答下列问题:
(1)、作的垂直平分线 , 分别交 , 于点E、F,垂足为点O(要求用尺规作图,保留作图痕迹.不要求写作法);(2)、若 , , 求的长.19. 我国的教育方针是:教育必须为社会主义现代化建设服务,为人民服务,与生产劳动和社会实践相结合,培养德智体美劳全面发展的社会主义建设者和接班人.为培养德智体美劳全面发展的优秀人才,丰都某中学开展了一系列精品课程,其中有一门课程《研学旅行》开展以来引起广泛关注,九年级2班数学兴趣小组对本班同学对《研学旅行》课的喜欢程度进行了调查,根据收集的数据绘制了两幅不完整的统计图,请根据图中信息,解答下列问题: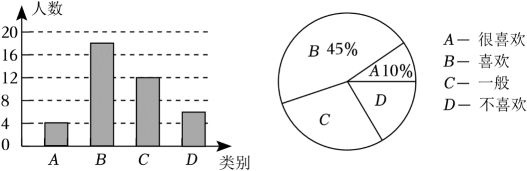 (1)、九年级2班共有学生名;(2)、九年级共有学生1200人,根据上述调查结果,估计九年级学生选择D类的大约有多少人?(3)、该校德育处决定从九年级二班调查的A类的4人中,抽2人到八年级开展研学宣讲,若在调查的A类4人中,刚好有2名男生2名女生,用画树状图或列表的方法求抽到的一男一女的概率.20. 某公司计划从商店购买台灯和手电筒,已知台灯的单价比手电筒的单价高50元,用240元购买台灯的数量和用90元购买手电筒的数量相等.(1)、求购买一盏台灯、一个手电筒各需要多少元?(2)、经商谈,商店给予该公司购买一盏台灯赠送一个手电筒的优惠.如果公司需要手电筒的数量是台灯数量的2倍还多8个,且购买台灯和手电筒的总费用不超过2440元,那么公司最多可购买多少盏台灯?21. 如图在平面直角坐标系中,直线AB:与反比例函数的图像交于A、B两点与x轴相交于点C,已知点A,B的坐标分别为和 .
(1)、九年级2班共有学生名;(2)、九年级共有学生1200人,根据上述调查结果,估计九年级学生选择D类的大约有多少人?(3)、该校德育处决定从九年级二班调查的A类的4人中,抽2人到八年级开展研学宣讲,若在调查的A类4人中,刚好有2名男生2名女生,用画树状图或列表的方法求抽到的一男一女的概率.20. 某公司计划从商店购买台灯和手电筒,已知台灯的单价比手电筒的单价高50元,用240元购买台灯的数量和用90元购买手电筒的数量相等.(1)、求购买一盏台灯、一个手电筒各需要多少元?(2)、经商谈,商店给予该公司购买一盏台灯赠送一个手电筒的优惠.如果公司需要手电筒的数量是台灯数量的2倍还多8个,且购买台灯和手电筒的总费用不超过2440元,那么公司最多可购买多少盏台灯?21. 如图在平面直角坐标系中,直线AB:与反比例函数的图像交于A、B两点与x轴相交于点C,已知点A,B的坐标分别为和 . (1)、求反比例函数的解析式;(2)、请直接写出不等式的解集;(3)、点P为反比例函数图像的任意一点,若 , 求点P的坐标.
(1)、求反比例函数的解析式;(2)、请直接写出不等式的解集;(3)、点P为反比例函数图像的任意一点,若 , 求点P的坐标.