安徽省江淮教育联盟2023年九年级第一次联考数学试卷
试卷更新日期:2023-04-18 类型:中考模拟
一、单选题
-
1. 下列各数中,比小的数是( )A、 B、 C、0 D、22. 计算的结果是( )A、 B、 C、 D、3. 下面四个几何体中,主视图为圆的是( )A、
 B、
B、 C、
C、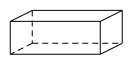 D、
D、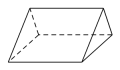 4. 第七次全国人口普查显示全国人口共141178万人,与2010年(第六次全国人口普查数据)的133972万人相比,增加7206万人,增长 , 年平均增长率为 , 将数据“141178万”用科学记数法表示为( )A、 B、 C、 D、5. 下列一元二次方程中,有两个不相等的实数根的是( )A、 B、 C、 D、6. 已知一次函数 , y随x的增大而增大,则a的值可以是( )A、 B、 C、0 D、7. 甲、乙、丙三人进行投篮比赛,现通过抽签决定出场顺序,则他们三人的比赛顺序恰好是甲、乙、丙的概率为( )A、 B、 C、 D、8. 某学生6次立定跳远的成绩(单位cm)如下:150,160,165,145,150,170.下列关于这组数据的描述错误的是( )A、众数是150 B、中位数是155 C、极差是20 D、平均数是9. 把一个长方体铁块放在如图所示的注满水的圆柱形容器内,容器底部有个水龙头,现打开水龙头按一定的速度放水,1min后将容器内水放完.那么容器内水面的高度与注水时间之间的函数关系图象大致是( )
4. 第七次全国人口普查显示全国人口共141178万人,与2010年(第六次全国人口普查数据)的133972万人相比,增加7206万人,增长 , 年平均增长率为 , 将数据“141178万”用科学记数法表示为( )A、 B、 C、 D、5. 下列一元二次方程中,有两个不相等的实数根的是( )A、 B、 C、 D、6. 已知一次函数 , y随x的增大而增大,则a的值可以是( )A、 B、 C、0 D、7. 甲、乙、丙三人进行投篮比赛,现通过抽签决定出场顺序,则他们三人的比赛顺序恰好是甲、乙、丙的概率为( )A、 B、 C、 D、8. 某学生6次立定跳远的成绩(单位cm)如下:150,160,165,145,150,170.下列关于这组数据的描述错误的是( )A、众数是150 B、中位数是155 C、极差是20 D、平均数是9. 把一个长方体铁块放在如图所示的注满水的圆柱形容器内,容器底部有个水龙头,现打开水龙头按一定的速度放水,1min后将容器内水放完.那么容器内水面的高度与注水时间之间的函数关系图象大致是( )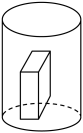 A、
A、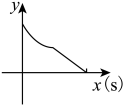 B、
B、 C、
C、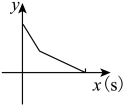 D、
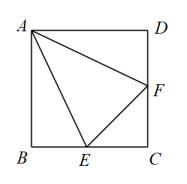
D、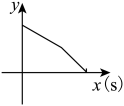 10. 如图,在中,、分别为斜边上的中线、高线,若 , , 则下列结论错误的是( )
10. 如图,在中,、分别为斜边上的中线、高线,若 , , 则下列结论错误的是( )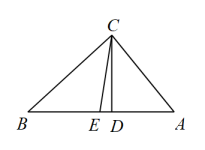 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算:= .
12. 因式分解: = .13. 在同一平面直角坐标系中,反比例函数与一次函数交于A、B两点,O为坐标原点,则的面积= .14. 如图,在矩形中, , , E为上一动点,F为延长线一点,且在E点运动中始终保持 .(1)、当时,则的长为;(2)、在此运动过程中,的比值为 .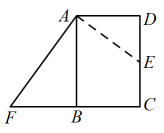
三、解答题
-
15. 计算:16. 解不等式, , 并把解集在数轴上表示出来.
 17. 如图,在平面坐标系内,三个顶点的坐标分别为 , , . 正方形网格中,每个小正方形的边长是1个单位长度
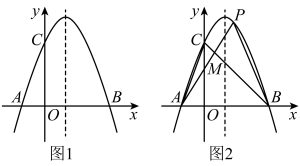
17. 如图,在平面坐标系内,三个顶点的坐标分别为 , , . 正方形网格中,每个小正方形的边长是1个单位长度 (1)、先将向下平移2个单位长度,再向左平移3个单位长度得到 , 请画出;(2)、与关于原点对称,请画出并直接写出点的长度.18. 观察以下等式:
(1)、先将向下平移2个单位长度,再向左平移3个单位长度得到 , 请画出;(2)、与关于原点对称,请画出并直接写出点的长度.18. 观察以下等式:第1个等式: ,
第2个等式: ,
第3个等式: ,
第4个等式: , ……
按照以上规律,解决下列问题:
(1)、写出第5个等式:;(2)、写出你猜想的第个等式(用含的等式表示),并证明.19. 如图,中,在斜边上选一点O为圆心画圆,此圆恰好经过点A,且与直角边相切于点D,连接、 . (1)、求证:;(2)、若 , , 求阴影部分图形的周长.20. 如图是某飞机的翼展示意图,四边形为梯形, , 经测得 , , , 求此飞机一个翼展的面积.
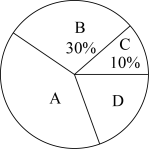
(1)、求证:;(2)、若 , , 求阴影部分图形的周长.20. 如图是某飞机的翼展示意图,四边形为梯形, , 经测得 , , , 求此飞机一个翼展的面积.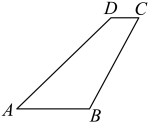 21. 某班为调查班级学生对A、B、C、D四项体育运动的喜爱情况,对全班同学进行了调查,每位同学只能选择一个最喜欢的运动,并把调查结果绘制成了统计表和扇形统计图.
21. 某班为调查班级学生对A、B、C、D四项体育运动的喜爱情况,对全班同学进行了调查,每位同学只能选择一个最喜欢的运动,并把调查结果绘制成了统计表和扇形统计图.男、女生最喜爱的体育运动人数统计表
目标
A
B
C
D
男生(人数)
12
3
5
女生(人数)
10
11
2
运动项目
频数
频率
A
22
B
C
5
0.1
D
总计
根据以上信息解决下列问题:
(1)、 , ;(2)、扇形统计图中A所对应扇形的圆心角度数为;(3)、从喜欢C的运动项目的5名学生中随机选取2名学生参加演讲,求所选取的2名学生中恰好有一名男生、一名女生的概率.