安徽省合肥市庐江县2023年初中毕业班九年级第一次教学质量抽测数学试题
试卷更新日期:2023-04-18 类型:中考模拟
一、单选题
-
1. 下列方程是一元二次方程的是( )A、 B、 C、 D、2. 彩民李大叔购买1张彩票,中奖这个事件是( )A、必然事件 B、确定性事件 C、不可能事件 D、随机事件3. 下列常用手机 APP 的图标中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 已知 , , 是抛物线上的点,则 , , 的大小关系为( )A、 B、 C、 D、5. 在⊙O中,P为其内一点,过点P的最长的弦为8cm,最短的弦长为4cm,则OP为.( )A、2cm B、cm C、3cm D、2cm6. 为执行“两免一补”政策,某地区2006年投入教育经费2500万元,预计2008年投入3600万元.设这两年投入教育经费的年平均增长百分率为x,则下列方程正确的是( )A、2500x2=3600 B、2500(1+x)2=3600 C、2500(1+x%)2=3600 D、2500(1+x)+2500(1+x)2=36007. 如图,在△ABC中,∠CAB=64°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′AB,则旋转角的度数为( )
4. 已知 , , 是抛物线上的点,则 , , 的大小关系为( )A、 B、 C、 D、5. 在⊙O中,P为其内一点,过点P的最长的弦为8cm,最短的弦长为4cm,则OP为.( )A、2cm B、cm C、3cm D、2cm6. 为执行“两免一补”政策,某地区2006年投入教育经费2500万元,预计2008年投入3600万元.设这两年投入教育经费的年平均增长百分率为x,则下列方程正确的是( )A、2500x2=3600 B、2500(1+x)2=3600 C、2500(1+x%)2=3600 D、2500(1+x)+2500(1+x)2=36007. 如图,在△ABC中,∠CAB=64°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′AB,则旋转角的度数为( ) A、64° B、52° C、42° D、36°8. 如图,在 的长方形网格飞镖游戏板中,每块小正方形除颜色外都相同,小正方形的顶点称为格点,扇形OAB的圆心及弧的两端均为格点.假设飞镖击中每一块小正方形是等可能的(击中扇形的边界或没有击中游戏板,则重投1次),任意投掷飞镖1次,飞镖击中扇形OAB(阴影部分)的概率是( )
A、64° B、52° C、42° D、36°8. 如图,在 的长方形网格飞镖游戏板中,每块小正方形除颜色外都相同,小正方形的顶点称为格点,扇形OAB的圆心及弧的两端均为格点.假设飞镖击中每一块小正方形是等可能的(击中扇形的边界或没有击中游戏板,则重投1次),任意投掷飞镖1次,飞镖击中扇形OAB(阴影部分)的概率是( )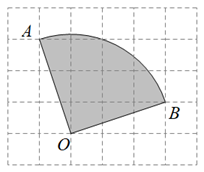 A、 B、 C、 D、9. 二次函数y=a(x-2)2+c与一次函数y=cx+a在同一坐标系中的大致图象是( )A、
A、 B、 C、 D、9. 二次函数y=a(x-2)2+c与一次函数y=cx+a在同一坐标系中的大致图象是( )A、 B、
B、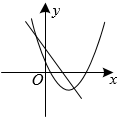 C、
C、 D、
D、 10. 如图,分别是半圆O的直径和弦, , , D是上的一个动点,连接AD.过点C作于E,连接 , 则的最小值是( )
10. 如图,分别是半圆O的直径和弦, , , D是上的一个动点,连接AD.过点C作于E,连接 , 则的最小值是( )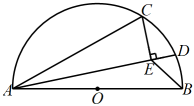 A、 B、 C、2 D、3
A、 B、 C、2 D、3二、填空题
-
11. 在平面直角坐标系中,点关于原点对称的点的坐标是 .12. 若一元二次方程有两个相等的实数根,则m= .13. 如图,三角形的顶点都在上,则的度数为 .
 14. 已知:抛物线 .(1)、此抛物线的对称轴为直线;(2)、当时,y的最小值为−4,则 .
14. 已知:抛物线 .(1)、此抛物线的对称轴为直线;(2)、当时,y的最小值为−4,则 .三、解答题
-
15. 解方程: .16. 已知某二次函数的图象的顶点为 , 且过点 .(1)、求此二次函数的关系式.(2)、判断点是否在这个二次函数的图象上,并说明理由.17. 如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,的顶点均在格点上.
 (1)、将绕点E逆时针旋转90°得到 , 画出 .(2)、若由绕着某点旋转得到的,则这点的坐标为 .18. 将黑色圆点按如图所示的规律进行排列,图中黑色圆点的个数依次为:1、3、6、10.…….按照以上规律,解决下列问题:
(1)、将绕点E逆时针旋转90°得到 , 画出 .(2)、若由绕着某点旋转得到的,则这点的坐标为 .18. 将黑色圆点按如图所示的规律进行排列,图中黑色圆点的个数依次为:1、3、6、10.…….按照以上规律,解决下列问题: (1)、第⑤个图中有个黑色圆点;第⑩个图中有个黑色圆点;(2)、第个图中有210个黑色圆点.19. 如图,是的直径,是的中点,于点 , 交于点F.
(1)、第⑤个图中有个黑色圆点;第⑩个图中有个黑色圆点;(2)、第个图中有210个黑色圆点.19. 如图,是的直径,是的中点,于点 , 交于点F. (1)、求证:;(2)、若 , 求弧的长度.20. 一人一盔安全守规,一人一带平安常在!某摩托车配件店经市场调查,发现进价为元的新款头盔每月的销售量件与售价元的相关信息如下:
(1)、求证:;(2)、若 , 求弧的长度.20. 一人一盔安全守规,一人一带平安常在!某摩托车配件店经市场调查,发现进价为元的新款头盔每月的销售量件与售价元的相关信息如下:售价x(元)
…
销售量y(件)
…
(1)、试用你学过的函数来描述与的关系,这个函数可以是(填“一次函数”或“二次函数”),写出这个函数解析式为 .(2)、若获利不得高于进价的 , 那么售价定为多少元时,月销售利润达到最大?21. 某商场为掌握元旦期间顾客购买商品时刻的分布情况,元旦当天将顾客购买商品的时刻t分四个时间段:7:0011:00,11:0015:00,15:0019:00和19:0023:00(分别记为A段,B段,C段和D段)统计了5000名顾客的购买时刻.并绘制出顾客购买商品时刻的扇形统计图和频数分布直方图如下,其中扇形统计图中,A,B,C,D四段各部分圆心角的度数比为1︰3︰4︰2.
请根据上述信息解答下列问题:
(1)、B段的顾客人数为人,C段的顾客人数为人;补全频数直方图;(2)、顾客购买商品时刻的中位数落在段(填写表示时间段的字母即可);(3)、为活跃节日气氛,该商场设置购物后抽奖活动,设立了特等奖一个,一等奖两个,二等奖若干,并随机分配到A,B,C,D四个时间段中.①请直接写出特等奖出现在A时间段的概率:;
②请利用画树状图或列表的方法,求两个一等奖出现在不同时间段的概率 .
22. 对于一个函数,自变量x取a时,函数值y也等于a,则称a是这个函数的不动点.已知抛物线 . (1)、若抛物线经过点 , 求该抛物线的顶点坐标;(2)、如图,在(1)的条件下,在x轴上方作平行于x轴的直线l,与抛物线交于B,C两点(点C在对称轴的右侧),过点B,C作x轴的垂线,垂足分别为E,D.当矩形为正方形时,求B点的坐标.(3)、若抛物线有两个相异的不动点a、b,且 , 求m的取值范围.23.(1)、如图1,过等边的顶点A作的垂线l,点P为l上点(不与点A重合),连接 , 将线段绕点C逆时针方向旋转60°得到线段 , 连接 .
(1)、若抛物线经过点 , 求该抛物线的顶点坐标;(2)、如图,在(1)的条件下,在x轴上方作平行于x轴的直线l,与抛物线交于B,C两点(点C在对称轴的右侧),过点B,C作x轴的垂线,垂足分别为E,D.当矩形为正方形时,求B点的坐标.(3)、若抛物线有两个相异的不动点a、b,且 , 求m的取值范围.23.(1)、如图1,过等边的顶点A作的垂线l,点P为l上点(不与点A重合),连接 , 将线段绕点C逆时针方向旋转60°得到线段 , 连接 .
①求证:;
②连接并延长交直线于点D.若 , , 求的长;
(2)、如图2,在中, , 将边绕点A顺时针旋转得到线段 , 连接 , 若 , , 求长.