广东省深圳市龙华区2022年中考数学模拟试卷

试卷更新日期：2023-04-18 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列实数中，最大的数是（）

A、 $π$ B、 $\sqrt{2}$ C、 $| - 2 |$ D、3

查看试题解析
2. 我国传统文化中的“福禄寿喜”，这四个图案中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 在“百度”中搜索“深圳先行示范区”，能搜索到与之相关的信息约21700000个，若将这数据21700000用科学记数法表示为（　　）

A、0.217×10⁹ B、2.17×10⁸ C、2.17×10⁷ D、217×10⁵

查看试题解析
4. 下列运算正确的是（）

A、（﹣a²）³=﹣a⁵ B、a³•a⁵=a¹⁵ C、（﹣a²b³）²=a⁴b⁶ D、3a²﹣2a²=1

查看试题解析
5. 如图，在矩形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 相交于点 $O$ ，已知 $∠ A C B = 25 °$ ，则 $∠ A O B$ 的大小是（）

A、 $130 °$ B、 $65 °$ C、 $50 °$ D、 $25 °$

查看试题解析
6. 关于一元二次方程 $x^{2} + 4 x + 3 = 0$ 根的情况，下列说法中正确的是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定

查看试题解析
7. 如图，点A的坐标为（1，3），点B在x轴上，把 $△ A O B$ 沿x轴向右平移到 $△ C E D$ ，若四边形ABDC的面积为9，则点C的坐标为（）

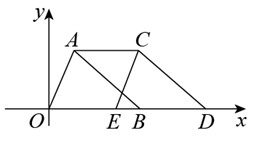A、（1，4） B、（3，4） C、（3，3） D、（4，3）

查看试题解析
8. 如图是某地滑雪运动场大跳台简化成的示意图．其中AB段是助滑坡，倾斜角 $∠ 1 = 37 °$ ，BC段是水平起跳台，CD段是着陆坡，倾斜角 $∠ 2 = 30 °$ ， $\sin 37 ° \approx 0.6$ ， $\cos 37 ° \approx 0.8$ ．若整个赛道长度（包括AB、BC、CD段）为270m，平台BC的长度是60m，整个赛道的垂直落差AN是114m．则AB段的长度大约是（）．

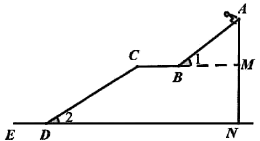A、80m B、85m C、90m D、95m

查看试题解析
9. 二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，其与x轴交于点A（m，0），点B，下列4个结论：① $b < 0$ ；② $m > - 2$ ；③ $a x^{2} + b x + c = - 1$ 有两个不相等的实数根；④ $\frac{c}{a} > - 3$ ．其中正确的是（）

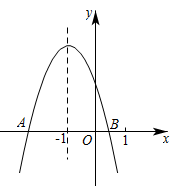A、①② B、①③ C、①③④ D、①②③④

查看试题解析
10. 如图，在矩形ABCD中，AD＝ $\sqrt{2}$ AB，∠BAD的平分线交BC于点E．DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，下列结论：①AD＝AE；②∠AED＝∠CED；③OE＝OD；④BH＝HF；⑤BC－CF＝2HE，其中正确的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

11. 分解因式： $2 m^{2} - 18 =$ .

查看试题解析
12. 在一个不透明的盒子中装有2个白球，n个黄球，它们除颜色不同外，其余均相同．若从中随机摸出一个球，它是黄球的概率为 $\frac{3}{4}$ ，则n＝．

查看试题解析
13. 如图，无人机于空中 $A$ 处测得某建筑顶部 $B$ 处的仰角为45°，测得该建筑底部 $C$ 处的俯角为35°.若无人机的飞行高度 $A D$ 为42m，则该建筑的高度 $B C$ 为 $m$ .（参考数据： $\sin 35 ° \approx 0.57$ ， $\cos 35 ° \approx 0.82$ ， $\tan 35 ° \approx 0.70$ ）.

查看试题解析
14. 若 $A (1 ， y_{1})$ ， $B (3 ， y_{2})$ 是反比例函数 $y = \frac{2 m - 1}{x} (m < \frac{1}{2})$ 图象上的两点，则 $y_{1}$ 、 $y_{2}$ 的大小关系是 $y_{1}$ $y_{2}$ （填“>”、“=”或“<”）

查看试题解析
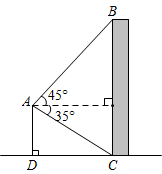15. 如图，弧AB所对圆心角∠AOB＝90°，半径为4，点C是OB中点，点D是弧AB上一点，CD绕点C逆时针旋转90°得到CE，则AE的最小值是.

查看试题解析

三、解答题

16. 计算： $(4 - \sqrt{3})^{0} - 3 t a n 60 ° - (- \frac{1}{2})^{- 1} + \sqrt{2}$ ．

查看试题解析
17. 解方程： $x^{2} - 4 x - 12 = 0$ .

查看试题解析
18. 感恩是中华民族的传统美德，学校在3月份提出了“感恩父母、感恩老师、感恩他人”感恩在行动教育活动．感恩行动有：A．由你为父母过一次有意义的生日；B．为班级设计一个班徽；C．主动找老师进行一次交流，谈一谈自己对于未来的憧憬；D．关注身边有需要帮助的同学，帮助有困难的同学渡过难关．为了了解学生对这4种感恩行动的选择情况，学校德育处在全校范围内随机抽取若干名学生，进行问卷调查（每个被调查的学生在4种感恩行动中只选择最喜欢做的一种），将数据进行整理并绘制成如下两幅统计图（未画完整）．

(1)、这次调查中，一共调查了名学生；

(2)、请补全扇形统计图中的数据及条形统计图；

(3)、本次九（1）班被抽样的学生一共5名同学，其中3名是选A的同学，1名是选C的同学，1名是选D的同学，班委会准备组织一次主题班会，要从这5名同学中随机选出2人在班会上介绍自己的行动方案，请通过树状图或列表求两人均是选A的概率．

查看试题解析
19. 某新型高科技商品，每件的售价比进价多6元，5件的进价相当于4件的售价，每天可售出200件，经市场调查发现，如果每件商品涨价1元，每天就会少卖5件．

(1)、该商品的售价和进价分别是多少元？

(2)、设每天的销售利润为w元，每件商品涨价a元，则当售价为多少元时，该商品每天的销售利润最大，最大利润为多少元？

查看试题解析
20. 如图，AB为 $⊙ O$ 直径， $C$ 为 $⊙ O$ 上的一点，过点 $C$ 的切线与AB的延长线相交于点D， $C A = C D$ .

(1)、连接BC，求证： $B C = O B$ ；

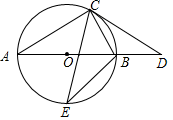(2)、 $E$ 是 $\overset{⌢}{A B}$ 中点，连接 $C E$ ，BE，若 $B E = 4$ ，求 $C E$ 的长.

查看试题解析
21. 【问题提出】如图（1），每一个图形中的小圆圈都按一定的规律排列，设每条边上的小圆圈个数为a，每个图形中小圆圈的总数为S．
请观察思考并完成以下表格的填写：
a
1
2
3
4
5
…
8
…
S
1
3
6
…
…

(1)、【变式探究】请运用你在图（1）中获得的经验，结合图（2）中小圆圈的排列规律，写出第n个图形的小圆圈总数S与n之间的关系式．

(2)、【应用拓展】生物学家在研究时发现，某种细胞的分裂规律可用图（3）的模型来描述，请写出经过n轮分裂后细胞总数W与n的关系式．并计算经过若干轮分裂后，细胞总数能否达到1261个，若能，求出n的值；若不能，说明理由．

查看试题解析
22. 如图（1），在Rt△ABC中，∠C＝90°，边AC＝8，BC＝6，点M、N分别在线段AC、BC上，将△ABC沿直线MN翻折，点C的对应点是C′．

(1)、当M、N分别是所在边的中点时，求线段CC′的长度；

(2)、若CN＝2，求点C′到线段AB的最短距离；

(3)、如图（2），当点C′落在边AB上时，
①四边形CMC′N能否成为正方形？若能，求出CM的值；若不能，说明理由．
②请直接写出点C′运动的路程长度．

查看试题解析

a	1	2	3	4	5	…	8	…
S	1	3	6			…		…