浙江省温州市鹿城区2023年九年级中考一模数学试题

试卷更新日期：2023-04-18 类型：中考模拟

进入出卷网下载

一、单选题

1. －5的相反数是（）

A、 $- \frac{1}{5}$ B、 $\frac{1}{5}$ C、5 D、-5

查看试题解析
2. 某款三角烧瓶如图所示，它的主视图是（）

A、 B、 C、 D、

查看试题解析
3. 某校九年级学生的视力情况统计如图所示，若中度近视的学生有80人，则轻度近视的学生有（）

A、40人 B、108人 C、120人 D、160人

查看试题解析
4. 一个不透明的袋子里装有3个红球，5个黑球和2个白球，它们除颜色外其余都相同.从袋中任意摸出一个球是红球的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{3}{7}$ C、 $\frac{3}{10}$ D、 $\frac{1}{5}$

查看试题解析
5. 如图， $A C$ 是 $⊙ O$ 的直径，B，D是 $⊙ O$ 上的两点，连接 $A B$ ， $B C$ ， $C D$ ， $B D$ ，若 $∠ A + ∠ D = 80 °$ ，则 $∠ A C B$ 的度数为（）

A、 $40 °$ B、 $50 °$ C、 $60 °$ D、 $80 °$

查看试题解析
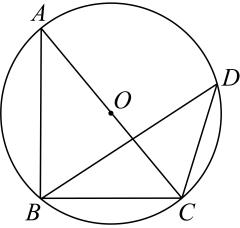6. 若关于x的方程 $2 x^{2} + 3 x + c = 0$ 没有实数根，则c的值可能为（）

A、 $- 1$ B、0 C、1 D、2

查看试题解析
7. 若干名学生一起去种树，如果每人种4棵，则还剩下3棵树苗：如果每人种5棵，则缺少5棵树苗.设学生有 $x$ 人，树苗有 $y$ 棵，根据题意可列出方程组（）

A、 ${\begin{array}{l} 4 x = y - 3 \\ 5 x = y + 5 \end{array}$ B、 ${\begin{array}{l} 4 x = y + 3 \\ 5 x = y - 5 \end{array}$ C、 ${\begin{array}{l} 5 x = y - 3 \\ 4 x = y + 5 \end{array}$ D、 ${\begin{array}{l} 5 x = y + 3 \\ 4 x = y - 5 \end{array}$

查看试题解析
8. 已知 $(2 ， y_{1})$ ， $(1 - m^{2} ， y_{2})$ ， $(4 + m^{2} ， y_{3})$ 是抛物线 $y = a x^{2} - 4 a x (a > 0)$ 上的三点，则下列结论中正确的是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{1} < y_{3} < y_{2}$ C、 $y_{2} < y_{3} < y_{1}$ D、 $y_{3} < y_{2} < y_{1}$

查看试题解析
9. 如图是一款汽车千斤顶，其主要部件为四根连杆组成的菱形 $A B C D$ 和螺旋杆 $P Q$ ，当 $B D = m$ ， $∠ C B D = α$ 时，A，C两点的距离为（）

A、 $\frac{m t a n α}{2}$ B、 $\frac{m s i n α}{2}$ C、 $m t a n α$ D、 $m s i n α$

查看试题解析
10. 由四个全等的直角三角形和一个小正方形组成的大正方形 $A B C D$ 如图所示，连接 $A G$ 并延长交 $C D$ 于点M，延长 $B G$ 交 $C D$ 于点N.若 $A E ： E F = 4 ： 5$ ，则 $A B$ 与 $M N$ 的比值为（）

A、 $\frac{16}{3}$ B、 $\frac{36}{7}$ C、 $\frac{45}{8}$ D、 $\frac{81}{16}$

查看试题解析

二、填空题

11. 因式分解：4m²-25＝．

查看试题解析
12. 若扇形的圆心角为90°，半径为3，则该扇形的弧长为.（结果保留 $π$ ）

查看试题解析
13. 某校对八年级部分学生每周体育锻炼时间进行抽查，得到频数直方图（每一组含前一个边界值，不含后一个边界值）如图所示，估计该校八年级900名学生每周体育锻炼时间至少8小时的有人.

查看试题解析
14. 为预防传染病，某校定期对教室进行“药熏消毒”.如图所示，药物燃烧阶段，教室内每立方米空气中的含药量 $y (m g)$ 与燃烧时间x（分）成正比例；燃烧后，y与x成反比例.若 $y > 1.6$ ，则x的取值范围是.

查看试题解析
15. 如图，在矩形 $A B C D$ 中，E，F是边 $B C$ 上两点（ $B F > B E$ ），H，G是边 $A D$ 上两点，且 $B E = C F = A H = D G$ ，连接 $A F$ ， $C H$ ， $B G$ ， $D E$ .若 $A B = 4$ ， $B C = 6$ ， $∠ B A F = 45 °$ ，则阴影部分的面积为.

查看试题解析
16. 一款闭门器按如图1所示安装，支点A，C分别固定在门框和门板上，门宽 $O D = 52 c m$ ，摇臂 $A B = 18 c m$ ，连杆 $B C = 24 c m$ ，闭门器工作时，摇臂、连杆和 $O C$ 长度均固定不变.如图2，当门闭合时， $s i n ∠ B = \frac{\sqrt{5}}{3}$ ，则 $A C$ 的长为cm.如图3，门板绕点O旋转，当 $∠ B = 90 °$ 时，点D到门框的距离 $D K = 48 c m$ ，则 $O C$ 的长为cm.

查看试题解析

三、解答题

17.

(1)、计算： ${(\frac{1}{3})}^{- 1} + \sqrt{18} + | - 2 | - 6 s i n 45 °$ ；

(2)、化简： ${(2 a + 1)}^{2} - 4 a (a + 1)$ .

查看试题解析
18. 如图，在 $△ A B C$ 中， $A B = A C$ ， D是 $B C$ 上一点，延长 $B C$ 至点E，使得 $∠ D A E = ∠ B A C$ ，延长 $A D$ 至点F，使得 $A F = A E$ .

(1)、求证： $△ A B F ≌ △ A C E$ ；

(2)、若 $A D ⊥ B C$ ， $D F = 15$ ， $B C = 16$ ，求 $C E$ 的长.

查看试题解析
19. 如图，在8×8的方格纸中，P，Q为格点， $△ A B C$ 的顶点均在格点上，请按要求画图.（注：图1，图2在答题卷上.）

(1)、在图1中画出 $△ A B C$ 平移后的格点三角形，使得点B的对应点是线段 $P Q$ 的中点.

(2)、在图2中画出 $△ A B C$ 平移后的格点 $△ D E F$ ，点A，B，C的对应点分别是点D，E，F， $△ D E F$ 满足以下两个条件：
①直线 $D E$ 经过线段 $P Q$ 的一个端点；

②三个顶点均不落在线段 $P Q$ 上.

查看试题解析

20. 某校“小数学家”评比由小论文、说题比赛、其它荣誉、现场考核四部分组成，各部分在总分中占比分别为20%，20%，20%，40%.九（1）班小鹿、小诚两位同学前三项的得分如下表.

姓名	小论文	说题比赛	其它荣誉
小鹿	80分	90分	25分
小诚	85分	85分	25分

(1)、在首次现场考核模拟中，小鹿得到91分，小诚得到98分，请分别计算两位同学首次模拟后的总分.

(2)、两位同学先后5次现场考核模拟的成绩情况如图所示.根据所学的统计知识，你推荐哪位同学参加校级“小数学家”评比？请说明理由.

查看试题解析

21. 如图，抛物线 $y = \frac{1}{3} {(x - 4)}^{2} + h$ 与x轴的一个交点为 $A (6 ， 0)$ ，与y轴交于点B.

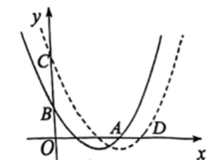(1)、求h的值及点B的坐标.

(2)、将该抛物线向右平移 $m (m > 0)$ 个单位长度后，与y轴交于点C，且点A的对应点为D，若 $O C = O D$ ，求m的值.

查看试题解析
22. 在 $△ A B C$ 中，D，E分别是 $A B$ ， $A C$ 的中点，延长 $E D$ 至点F，使得 $D F = D E$ ，连接 $B F$ .

(1)、求证：四边形 $B C E F$ 是平行四边形.

(2)、 $B G ⊥ C E$ 于点G，连接 $C F$ ，若G是 $C E$ 的中点， $C F = 6$ ， $t a n ∠ B C G = 3$ ，求 $▱ B C E F$ 的周长.

查看试题解析
23. 根据信息，完成活动任务.
活动一探究某地正午太阳光下长方体高度与影子的关系.
如图1是长方体在正午阳光下投影情况，图2是图1的俯视图，通过实验测得一组数据如下表所示：
$A B$ 的长（cm）
$10$
$20$
$30$
$40$
$50$
$B C$ 的长（cm）
$15$
30
$45$
$60$
$75$
$s i n ∠ B C D$
$0.8$
$0.8$
$0.8$
$0.8$
$0.8$

(1)、【任务1】如图2，作 $B H ⊥ C D$ 于点 $H$ ，设 $B H = y (c m)$ ， $A B = x (c m)$ ，求y关于x的函数表达式.

(2)、活动二设计该地房子的数量与层数.
在长方形土地上按图3所示设计n幢房子，已知每幢房子形状、高度相同，可近似看成长方体，图中阴影部分为1号楼的影子，相关数据如图所示.现要求每幢楼层数不超过 $24$ ，每层楼高度为3米.
【任务2】当1号楼层数为 $24$ 时，请通过计算说明正午时1号楼的影子是否落在2号楼的墙上.

(3)、【任务3】请你按下列要求设计，并完成表格.
①所有房子层数总和超过 $160$ .
②正午时每幢房子的影子不会落在相邻房子的墙上.
方案设计
每幢楼层数
n的值
层数总和

查看试题解析
24. 问题：如图，在 $△ A B C$ 中， $A C = B C = 5$ ， $A B = 6$ ， D在 $A B$ 延长线上， $D E ⊥ A D$ 于点D，过B，C，D三点的 $⊙ O$ 交 $D E$ 于点F，连结 $C D$ ， $C F$ .当 $△ C D F$ 为等腰三角形时，求 $B D$ 的长.

思路：小明在探索该问题时，发现 $∠ C F D = ∠ C B A$ ，于是作 $C H ⊥ D F$ 于点H，然后分步求解.

（1）设 $B D = x$ ，用x的代数式分别表示 $C H$ 和 $F H$ .

（2）当 $△ C D F$ 为等腰三角形时，求x的值.

(1)、请完成上述各步骤的解答.

(2)、

拓展：小明发现点A关于 $C D$ 的对称点始终落在 $⊙ O$ 上，于是他设计了如下问题：“当点A关于 $C D$ 的对称点 $A^{'}$ 恰为 $\overset{⌢}{C F}$ 的中点时，求 $B D$ 的长”，请完成该题的解答.

查看试题解析

$A B$ 的长（cm）	$10$	$20$	$30$	$40$	$50$
$B C$ 的长（cm）	$15$	30	$45$	$60$	$75$
$s i n ∠ B C D$	$0.8$	$0.8$	$0.8$	$0.8$	$0.8$

方案设计
每幢楼层数	n的值	层数总和