浙江省温州市文成县2023年中考一模数学试题

试卷更新日期：2023-04-18 类型：中考模拟

进入出卷网下载

一、单选题

1. -3的相反数是（）。

A、3 B、 $\frac{1}{3}$ C、-3 D、 $- \frac{1}{3}$

查看试题解析
2. 如图所示的几何体由一个圆柱体和一个长方体组成，它的俯视图是（）

A、 B、 C、 D、

查看试题解析
3. 计算 $m^{6} \div m^{3}$ 的结果是（）

A、 $m^{18}$ B、 $m^{9}$ C、 $m^{2}$ D、 $m^{3}$

查看试题解析
4. 温州银泰商场某店一天中卖出某种品牌的休闲鞋16双，它们的尺码与销售量如表所示：
鞋的尺码/cm
25
25.5
26
26.5
27
销售量/双
2
3
4
4
3
则这16双鞋的尺码组成的数据中，中位数（）

A、 $25.5 c m$ B、 $26 c m$ C、 $26.5 c m$ D、 $27 c m$

查看试题解析
5. 在平面直角坐标系中，有四个点 $A (2 ， 5)$ ， $B (1 ， 3)$ ， $C (3 ， 1)$ ， $D (- 2 ， - 3)$ ，其中不在同一个一次函数图象上的是（）

A、点A B、点B C、点C D、点D

查看试题解析
6. 如图， $△ A B C$ 内接于 $⊙ O$ ， $A B = A C$ ， $∠ B = 70 °$ ，则 $∠ O C B$ 等于（）

A、 $40 °$ B、 $50 °$ C、 $60 °$ D、 $65 °$

查看试题解析
7. 一张小凳子的结构如图所示， $A C = B C$ ， $∠ 1 = 100 °$ ， $B C = 20 c m$ ，则 $A B$ 等于（）.

A、 $20 s i n 50 ° c m$ B、 $40 c o s 50 ° c m$ C、 $\frac{20}{s i n 50 °} c m$ D、 $\frac{40}{c o s 50 °} c m$

查看试题解析
8. 如图， $O C$ 平分 $∠ A O B$ ， $A C = B C$ ，若 $O A = 7$ ， $O B = 3$ ， $A C = 2.5$ ，则点C到 $O A$ 边距离等于（）

A、 $1.5$ B、 $2$ C、 $\frac{\sqrt{5}}{2}$ D、 $\sqrt{5}$

查看试题解析
9. 已知点 $A (- 2 ， a)$ ， $B (- 1 ， b)$ ， $C (5 ， c)$ 是二次函数 $y = m x^{2} - 2 m x + n (m < 0)$ 上的点，则（）

A、 $a < c < b$ B、 $c < b < a$ C、 $a < b < c$ D、 $c < a < b$

查看试题解析
10. 由四个全等的直角三角形和一个小正方形组成的大正方形 $A B C D$ 如图所示.点E为小正方形的顶点，延长 $C E$ 交 $A D$ 于点F， $B F$ 分别交 $A M$ ， $D N$ 于点G，H，过点D作 $D N$ 的垂线交 $B F$ 延长线于点K，连结 $E K$ .若 $△ B C F$ 为等腰三角形， $A G = \frac{5}{2}$ ，则 $\frac{E K}{D H}$ 的值为（）

A、 $\frac{3}{2}$ B、 $\frac{6}{5}$ C、 $\frac{\sqrt{97}}{8}$ D、 $\frac{3 \sqrt{97}}{20}$

查看试题解析

二、填空题

11. 分解因式： $a^{2} - 1$ =.

查看试题解析
12. 数据 $1$ ， $3$ ， $2$ ， $3$ ， $7$ ， $a$ ， $5$ ， $3$ ，其中a是这组数据的众数，则该组数据的平均数是.

查看试题解析
13. 计算： $\frac{x^{2} + 2 x}{x + y} + \frac{2 y - x^{2}}{x + y} =$ .

查看试题解析
14. 如图，正六边形 $A B C D E F$ 内接于半径为1的 $⊙ O$ ，则 $\overset{⌢}{A B C}$ 的长为.

查看试题解析
15. 如图，点B在反比例函数 $y = \frac{k}{x} (k > 0 ， x > 0)$ 的图象上，点A在x轴上， $O B = A B$ ，过点A作 $A D ∥ O B$ 交y轴负半轴于点D，连结 $B D$ .当 $△ O C D$ 面积为3时，则k的值为.

查看试题解析
16. 图1是小文家的木马玩具，图2是木马玩具底座水平放置的示意图，点O是 $\overset{⌢}{A B}$ 所在圆的圆心， $O A = O B$ ，点A，点B离地高度均为 $15 c m$ ，水平距离 $A B = 90 c m$ .则 $O A =$ $c m$ .当半径 $O A$ 转到竖直位置时，木马就有翻倒的风险，为安全起见，点B离地高度应小于 $c m$ .

查看试题解析

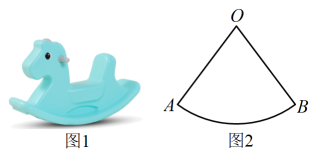
三、解答题

17.

(1)、计算： $2 \times (- 1) + \sqrt{9} + {(\sqrt{5})}^{0} - 2 s i n 30 °$ ；

(2)、化简： ${(m - 2)}^{2} - m (m + 4)$ .

查看试题解析
18. 如图，在四边形 $A B C D$ 中， $B D$ 平分 $∠ A D C$ ，点E在线段 $B D$ 上， $∠ A = ∠ D E C = 90 °$ ， $A B = C E$ .

(1)、求证： $△ A B D ≌ △ E C D$ ；

(2)、当 $∠ D C B = 55 °$ 时，求 $∠ A B D$ 的度数.

查看试题解析
19. 为关注学生出行安全，调查了某班学生出行方式，调查结果分为四类：A-骑自行车，B-步行，C-坐社区巴士，D-其它，并将调查结果绘制成以下两幅不完整的统计图.

请你根据统计图，解答下列问题：

(1)、本次一共调查了多少名学生？

(2)、C类女生有　　名，D类男生有　　名，并将条形统计图补充完整.

(3)、若从被调查的A类和D类学生中分别随机选取一位同学进行进一步调查，请用列表法或画树状图的方法求出所选同学中恰好是一位男同学和一位女同学的概率.

查看试题解析
20. 如图，在 $7 \times 5$ 的方格纸 $A B C D$ 中，请按要求画格点线段（端点在格点上），且线段的端点均不与点A，B，C，D重合.

(1)、在图1中画一条格点线段 $G H$ ，使G，H分别落在边 $A D$ ， $B C$ 上，且 $G H$ 与 $E F$ 互相平分.

(2)、在图2上画一条格点线段 $M N$ ，使M，N分别落在边 $A B$ ， $C D$ 上，且要求 $M N$ 分 $E F$ 为 $1 ： 2$ 两部分.

查看试题解析
21. 抛物线 $y = a x^{2} + b x - 3$ 经过点 $(- 2 ， 5)$ ， $(1 ， - 4)$ .

(1)、求a，b的值.

(2)、当 $- 1 \leq x \leq m$ 时，y最大值与最小值差为5，求m的值.

查看试题解析
22. 如图， $A B$ 为 $⊙ O$ 的直径，弦 $C D ⊥ A B$ 于点E，点F为圆上一点， $\overset{⌢}{A D} = \overset{⌢}{D F}$ ，过点C作 $C H ∥ A F$ 交 $A B$ 于点G，交 $A D$ 于点H.

(1)、求证： $C D = C H$ .

(2)、若 $C G = 2 G H$ ， $A B = 10$ ，求 $A F$ .

查看试题解析

23. 根据以下素材，探索完成任务.

如何给桥护栏挂小彩灯
素材1	图1是桥的护栏实物图，护栏长200米，高1.6米，图2是桥护栏示意图，为了使彩灯挂起来整齐美观，设计小组首先制作了外缘呈抛物线型模板，然后用该模板在图纸上绘制抛物线图案，彩灯沿抛物线摆放
素材2	方案一：护栏中间正好可以摆5具模板，绘制5条抛物线图案连成一条波浪线，每条抛物线的顶点落在护栏的上下边方案二：将模板一部分放入护栏，绘制若干条抛物线图案，靠上下两边连成两条波浪线，每条抛物线的高度都相等，相对两条抛物线的顶点之间的距离h为0.7米. 方案三：将方案一和方案二中的抛物线图案各若干条，沿护栏下边摆放，大的图案摆在中间，小的图案摆两边，连成一条波浪线，且整个小彩灯图案呈轴对称图形，每条抛物线图案保持完整，两边能摆尽摆，可以有空余
任务	问题解决
一	确定抛物线形状	求出模板抛物线的函数解析式
二	确定方案二中一条抛物线图案的宽度和摆放方案	求出其中一条抛物线图案的宽度 $C D$ .每边这样的图案最多可以摆放几个？
三	设计方案三摆放方案	确定大小抛物线图案各需多少个，并给出摆放方案

查看试题解析

24. 如图，点E，F分别为矩形 $A B C D$ 边 $A D$ ， $C D$ 上的点，以 $B E$ 为直径作 $⊙ O$ 交 $B F$ 于点G，且 $E F$ 与 $⊙ O$ 相切，连结 $E G$ .

(1)、若 $A E = E G$ ，求证： $△ A B E ≌ △ G B E$ .

(2)、若 $A B = 2$ ， $t a n ∠ E B F = \frac{1}{2}$ .
①求 $D E$ 的长.
②连结 $A G$ ，若 $△ A B G$ 是以 $A G$ 为腰的等腰三角形，求所有满足条件的 $B C$ 的长.

(3)、连结 $C G$ ，若 $C G$ 的延长线经过点A，且 $E D = E G$ ，求 $\frac{C G}{E F}$ 的值.

查看试题解析

鞋的尺码/cm	25	25.5	26	26.5	27
销售量/双	2	3	4	4	3