浙江省宁波市镇海区蛟川书院2023年九年级数学第一次模拟试题

试卷更新日期：2023-04-18 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算 $\frac{a^{2}}{a - 1} - a - 1$ 的正确结果是（）

A、 $- \frac{1}{a - 1}$ B、 $\frac{1}{a - 1}$ C、 $- \frac{2 a - 1}{a - 1}$ D、 $\frac{2 a - 1}{a - 1}$

查看试题解析
2. 下列长度的三条线段不能组成直角三角形的是（）

A、 $3 c m ， 4 c m ， 5 c m$ B、 $4 c m ， 3 c m ， \sqrt{7} c m$ C、 $6 c m ， 8 c m ， 9 c m$ D、 $1 c m$ ， $\sqrt{2} c m$ ， $\sqrt{3} c m$

查看试题解析
3. 已知 $9^{m} = 2$ ， $9^{- n} = 5$ ，则 $3^{4 m - 2 n}$ 的值是（）

A、 $\frac{16}{5}$ B、20 C、10 D、50

查看试题解析
4. 关于x，y 的方程组 ${\begin{array}{l} 2 a x + 3 y = 18 \\ - x + 5 b y = 17 \end{array}$ （其中a，b是常数）的解为 ${\begin{array}{l} x = 3 \\ y = 4 \end{array}$ ，则方程组 ${\begin{array}{l} 2 a (x + y) + 3 (x - y) = 18 \\ (x + y) - 5 b (x - y) = - 17 \end{array}$ 的解为（　　）

A、 ${\begin{array}{l} x = 3 \\ y = 4 \end{array}$ B、 ${\begin{array}{l} x = 7 \\ y = - 1 \end{array}$ C、 ${\begin{array}{l} x = 3.5 \\ y = - 0.5 \end{array}$ D、 ${\begin{array}{l} x = 3.5 \\ y = 0.5 \end{array}$

查看试题解析
5. 若 $x^{2} + y^{2} = 1$ ，则 $\sqrt{x^{2} - 4 x + 4} + \sqrt{x y - 3 x + y - 3}$ 的值为（）

A、0 B、1 C、2 D、3

查看试题解析
6. 如果 $x^{3} + a x^{2} + b x + 8$ 能被 $x^{2} + 3 x + 2$ 整除，则 $\frac{b}{a}$ 的值是（）

A、2 B、 $\frac{1}{2}$ C、3 D、 $\frac{1}{3}$

查看试题解析
7. 如图所示，满足函数 $y = k (x - 1)$ 和 $y = \f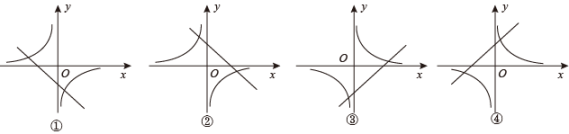rac{k}{x} (k \neq 0)$ 的大致图象是（）

A、①② B、②③ C、②④ D、①④

查看试题解析
8. $y = \sqrt{3} x$ 与 $y = \frac{k}{x}$ 交于A、B两点， $A C ⊥ A B$ 交y轴于点C， $B C$ 延长线交双曲线于点D，若 $B D = 5$ ，则 $A D$ 为（）

A、2 B、3 C、 $\sqrt{3}$ D、 $\frac{5}{3} \sqrt{3}$

查看试题解析
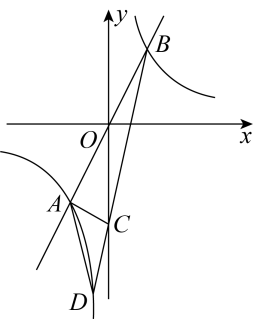9. $A B = \sqrt{2}$ ， AC＝1，以BC为边作正方形BCED，当线段AC绕点A任意旋转时，正方形BCED也随之旋转，若x＝AD＋AE，则x的取值范围是（）

A、 $1 \leq x \leq 2 + 3 \sqrt{2}$ B、 $1 \leq x \leq 3 + 2 \sqrt{2}$ C、 $1 \leq x \leq 3 + 3 \sqrt{2}$ D、 $1 \leq x \leq 2 + 2 \sqrt{2}$

查看试题解析
10. 如图， $⊙ O$ 的直径AB， $C D$ 垂直平分OA，AB延长线上一点E，DE交圆O于F，且 $E F = O A$ .弦DH交OC于G，满足 $G D^{2} = G O \times G E$ ， $S_{△ D H F} - S_{△ D C E} = 2 \sqrt{3}$ ， AC长为（）

A、 $\sqrt{3}$ B、 $\frac{4}{3} \sqrt{3}$ C、2 D、 $2 \sqrt{3}$

查看试题解析

二、填空题

11. 已知 ${(a^{2} + b^{2})}^{2} - a^{2} - b^{2} - 6 = 0$ ，求 $a^{2} + b^{2}$ 的值为.

查看试题解析
12. 燃放烟花爆竹是中国春节的传统民俗，在江北区一烟花爆竹销售点了解到，某种品牌的烟花 $2021$ 除夕每箱进价 $100$ 元，售价 $250$ 元，销售量 $40$ 箱.而 $2022$ 年除夕当天和去年当天相比，该店的销售量下降了 $4 a %$ （a为正整数），每箱售价提高了 $a %$ ，成本增加了 $50 %$ ，其销售利润仅为去年当天利润的 $50 %$ .则a的值为.

查看试题解析
13. △ABC，D为AC中点，BA=BD，DE⊥AC交C于E，EA交BD于F， $t a n ∠ E A B = \frac{1}{2}$ ， FD=5，则AF=.

查看试题解析
14. 如图， $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 4 ， B C = 3$ ，点D、E分别在直线 $A C$ ， $A B$ 上，连接 $D E$ ，将 $△ A D E$ 沿 $D E$ 翻折，使点A对应点 $A^{'}$ .当 $A^{'} D ⊥ A C$ ，且 $C A^{'} ∥ A B$ 时， $A E =$ ， $A D =$ .

查看试题解析
15. 如图，矩形 $A B C D$ 的两条对角线 $A C ， B D$ 相交于点O， $O E ⊥ A B$ ，垂足为E，F是 $O C$ 的中点，连接 $E F$ 交 $O B$ 于点P，那么 $\frac{O P}{P B} =$ .

查看试题解析
16. 如图， $R t △ A B C$ 中， $A B = A C = 12 \sqrt{2}$ ， $R t △ A D E$ 中， $A D = A E = 6 \sqrt{2}$ ，直线 $B D$ 与 $C E$ 交于P，当 $∠ E A D$ 绕点A任意旋转的过程中，P到直线 $A B$ 距离的最大值是.

查看试题解析

三、解答题

17. 解方程：

(1)、 $\frac{1 - x}{x - 2} = \frac{1}{2 - x} - 2$ ；

(2)、 $\frac{x + 5}{x + 4} + \frac{x + 2}{x + 1} = \frac{x + 3}{x + 2} + \frac{x + 4}{x + 3}$ .

查看试题解析
18. 在 $3 \times 5$ 的网格中，小正方形的顶点称为格点.如图，A，B是格点，画等腰 $△ A B C$ ，使点C是格点，且分别满足下列条件：

(1)、 $A C = A B$ （画在图①中）；

(2)、 $△ A B C$ 的面积为5（画在图②中）；

(3)、使 $△ A B C$ 的面积最大（画在图③中）.

查看试题解析
19. 某市为了提升菜篮子工程质量，计划用大、中型车辆共30辆调拨不超过190吨蔬菜和162吨肉制品补充当地市场.已知一辆大型车可运蔬菜8吨和肉制品5吨；一辆中型车可运蔬菜3吨和肉制品6吨.

(1)、符合题意的运输方案有几种？请你帮助设计出来；

(2)、若一辆大型车的运费是900元，一辆中型车的运费为600元，试说明（1）中哪种运输方案费用最低？最低费用是多少元？

查看试题解析
20. 如图，一次函数y=kx+b（k≠0）的图象与x轴，y轴分别交于A（-9，0），B（0，6）两点，过点C（2，0）作直线l与BC垂直，点E在直线l位于x轴上方的部分.

(1)、求一次函数y=kx+b（k≠0）的表达式；

(2)、若△ACE的面积为11，求点E的坐标；

(3)、当∠CBE=∠ABO时，点E的坐标为.

查看试题解析
21. 如图，在 $△ A B C$ 中， $\frac{B C}{A C} = \frac{2}{3}$ ， D，M，N分别在直线 $A B$ ，直线 $A C$ ，直线 $B C$ 上，

(1)、若D是 $A B$ 中点， $∠ M D N = ∠ A + ∠ B$ ，求 $\frac{M D}{N D}$ ；

(2)、若点D，M，N分别在 $A B$ ， $C A$ ， $C B$ 的延长线上，且 $\frac{A B}{B D} = \frac{3}{4}$ ， $∠ M D N = ∠ A C B$ ，求 $\frac{M D}{N D}$ .

查看试题解析
22. A，B在半径为 $4$ 的 $⊙ O$ 上， $∠ A O B = 90 °$ ， C在劣弧 $A B$ 上， $A C$ 、 $O B$ 延长线交于点D，连结 $B C$ .

(1)、求 $∠ B C D$ 的度数；

(2)、若 $A C = x$ ， $B D = y$ ，求y与x的关系式；

(3)、 $O M = \sqrt{3}$ ，以M为圆心的圆经过点A，C.当 $B D = (\sqrt{3} - 1) O B$ 时，求 $⊙ M$ 的半径.

查看试题解析
23. 如图，抛物线 $y = a x^{2} - 8 a x + 12 a (a < 0)$ 与x轴交于A，B两点（点A在点B的左侧），抛物线上另有一点C在第一象限，满足 $∠ A C B$ 为直角，且使 $∠ O C A ＝ ∠ O B C$ .

(1)、求线段OC的长；

(2)、求该抛物线的函数关系式；

(3)、在抛物线的对称轴上是否存在一点P，使得 $△ B C P$ 是以 $B C$ 为腰的等腰三角形？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由.

查看试题解析
24. 如图， $A B ， B C ， C D$ 分别与 $⊙ O$ 相切于E，F，G三点，且 $E G$ 为 $⊙ O$ 的直径.

(1)、延长 $O F ， E B$ 交于点P，若 $B E = 1$ ， $∠ E B F = 2 ∠ O P C$ ，求图中阴影部分的面积；

(2)、连接 $B G$ ，与 $O F$ 交于点M，若 $B E = 1 ， O E = 2$ ，求 $\frac{B M}{M G}$ 的值.

查看试题解析