浙江省金华市六校联谊2023年中考模拟数学试题
试卷更新日期:2023-04-18 类型:中考模拟
一、单选题
-
1. 给出四个数0 , , , 3,其中为无理数的是( )A、0 B、 C、3 D、2. 在科幻小说《三体》中,制造太空电梯的材料是由科学家汪淼发明的一种只有头发丝粗细的超高强度纳米丝“飞刃”,已知正常的头发丝直径为 , 则“飞刃”的直径()用科学记数法表示为( )A、 B、 C、 D、3. 下列几何体中,主视图是矩形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 关于x的方程x(x﹣1)=3(x﹣1),下列解法完全正确的是( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 关于x的方程x(x﹣1)=3(x﹣1),下列解法完全正确的是( )A
B
C
D
两边同时除以(x﹣1)得,x=3
整理得,x2﹣4x=﹣3∵a=1,b=﹣4,c=﹣3,
b2﹣4ac=28
∴x==2±
整理得,x2﹣4x=﹣3配方得,x2﹣4x+2=﹣1
∴(x﹣2)2=﹣1
∴x﹣2=±1
∴x1=1,x2=3
移项得,(x﹣3)(x﹣1)=0∴x﹣3=0或x﹣1=0
∴x1=1,x2=3
A、A B、B C、C D、D6. 下列条件中,能判定为直角三角形的是( )A、 B、 C、:::: D、 ,7. 经过某十字路口的的汽车,它可能继续直行,也可能向左或向右转,若这三种可能性相同.则甲乙两辆汽车经过该十字路口全部继续直行的概率为( )A、 B、 C、 D、8. 消防云梯如图所示,AB⊥BC于B,当C点刚好在A点的正上方时,DF的长是.( ) A、 B、 C、 D、9. 设双曲线(k > 0)与直线y=x交于A,B两点(点A在第三象限),将双曲线在第一象限的一支沿射线BA的方向平移,使其经过点A,将双曲线在第三象限的一支沿射线AB的方向平移,使其经过点B,平移后的两条曲线相交于点P,Q两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,PQ为双曲线的“眸径”.当双曲线(k > 0)的眸径为4时,k的值为( )
A、 B、 C、 D、9. 设双曲线(k > 0)与直线y=x交于A,B两点(点A在第三象限),将双曲线在第一象限的一支沿射线BA的方向平移,使其经过点A,将双曲线在第三象限的一支沿射线AB的方向平移,使其经过点B,平移后的两条曲线相交于点P,Q两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,PQ为双曲线的“眸径”.当双曲线(k > 0)的眸径为4时,k的值为( ) A、 B、 C、2 D、410. 由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.作.若 , 则的值为( )
A、 B、 C、2 D、410. 由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.作.若 , 则的值为( )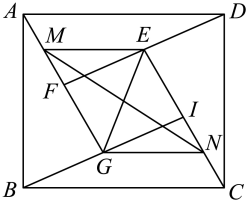 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 二次根式 中,x的取值范围是 .12. 已知线段a=2,b=8,则a,b的比例中项线段长是 .13. 某校学生“数学素养”大赛成绩的频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中成绩为“一般”(80分以下)的学生有人.
 14. 如图,点O是半圆圆心,是半圆的直径,点A,D在半圆上,且 , 过点D作于点C,则阴影部分的面积是.
14. 如图,点O是半圆圆心,是半圆的直径,点A,D在半圆上,且 , 过点D作于点C,则阴影部分的面积是. 15. 在平面直角坐标系中,过一点分别作坐标轴的垂线,若垂线与坐标轴围成矩形的周长的值与面积的值相等,则这个点叫做“和美点”.已知直线与轴交于点A,与反比例函数的图象交于点 , 且点是“和美点”,则的面积为.16. 如图,为一条宽为4米的河,河的西岸建有一道防洪堤、防洪堤与东岸的高度差为3米(即米),因为施工需要,现准备将东岸的泥沙将通过滑轨送到西岸的防洪堤上,防洪堤上已经建好一座固定滑轨一端的钢架,现准备在东岸找一个点P作为另一端的固定点,已知吊篮的截面为直径为1米的半圆(直径米),绳子米,钢架高度2. 2米(米),距离防洪堤边缘为 0. 5米(米),
15. 在平面直角坐标系中,过一点分别作坐标轴的垂线,若垂线与坐标轴围成矩形的周长的值与面积的值相等,则这个点叫做“和美点”.已知直线与轴交于点A,与反比例函数的图象交于点 , 且点是“和美点”,则的面积为.16. 如图,为一条宽为4米的河,河的西岸建有一道防洪堤、防洪堤与东岸的高度差为3米(即米),因为施工需要,现准备将东岸的泥沙将通过滑轨送到西岸的防洪堤上,防洪堤上已经建好一座固定滑轨一端的钢架,现准备在东岸找一个点P作为另一端的固定点,已知吊篮的截面为直径为1米的半圆(直径米),绳子米,钢架高度2. 2米(米),距离防洪堤边缘为 0. 5米(米), (1)、西岸边缘点C与东岸边缘点D之间的距离为米;(2)、滑轨在运送货物时保持笔直,要想做到运输过程中吊篮一定不会碰到点C, 则的长度至少保持米.
(1)、西岸边缘点C与东岸边缘点D之间的距离为米;(2)、滑轨在运送货物时保持笔直,要想做到运输过程中吊篮一定不会碰到点C, 则的长度至少保持米.三、解答题
-
17. 计算:.18. 先化简,再求值: , 其中.19. 如图,六个完全相同的小长方形(长是宽的2倍)拼成了一个大长方形,是其中一个小长方形的对角线,请在大长方形中按要求完成下列作图:①仅用无刻度直尺,且不能用直尺的直角;②保留必要的画图痕迹;③标注字母.
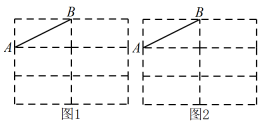 (1)、在图1中画出一个以为直角边的直角三角形.(2)、在图2中画出一个以为底边的等腰三角形.20. 如图,下列装在相同的透明密封盒内的古钱币,其密封盒上分别标有古钱币的尺寸及质量,例如:钱币“文星高照”密封盒上所标“”是指该枚古钱币的直径为 , 厚度为 , 质量为.已知这些古钱币的材质相同.
(1)、在图1中画出一个以为直角边的直角三角形.(2)、在图2中画出一个以为底边的等腰三角形.20. 如图,下列装在相同的透明密封盒内的古钱币,其密封盒上分别标有古钱币的尺寸及质量,例如:钱币“文星高照”密封盒上所标“”是指该枚古钱币的直径为 , 厚度为 , 质量为.已知这些古钱币的材质相同.
根据图中信息,解决下列问题.
(1)、这5枚古钱币,所标直径的平均数是 , 所标厚度的众数是 , 所标质量的中位数是 g;(2)、由于古钱币无法从密封盒内取出,为判断密封盒上所标古钱币的质量是否有错,桐桐用电子秤测得每枚古钱币与其密封盒的总质量如下:名称
文星高照
状元及第
鹿鹤同春
顺风大吉
连中三元
总质量/g
58.7
58.1
55.2
54.3
55.8
请你应用所学的统计知识,判断哪枚古钱币所标的质量与实际质量差异较大,并计算该枚古钱币的实际质量约为多少克.
21. 如图,是的直径,是的切线,切点为B,连接PO,过点C作交于点A,连接. (1)、求证:是的切线;(2)、若 , 的半径为3,求的长.22. 如图,排球运动员站在点O处练习发球,将球从O点正上方的A处发出,把球看成点,其运行的高度与运行的水平距离满足关系式.已知球网与O点的水平距离为 , 高度为 , 球场的边界距O点的水平距离为.
(1)、求证:是的切线;(2)、若 , 的半径为3,求的长.22. 如图,排球运动员站在点O处练习发球,将球从O点正上方的A处发出,把球看成点,其运行的高度与运行的水平距离满足关系式.已知球网与O点的水平距离为 , 高度为 , 球场的边界距O点的水平距离为. (1)、当时,求y与x的关系式(不要求写出自变量x的取值范围);(2)、当时,球能否越过球网?球会不会出界?请说明理由;(3)、若球一定能越过球网,又不出边界,求h的取值范围.23. 在平面直角坐标系中,某个函数图象上任意两点的坐标分别为和(其中t为常数且),将的部分沿直线翻折,翻折后的图象记为;将的部分沿直线翻折,翻折后的图象记为 , 将和及原函数图象剩余的部分组成新的图象G.
(1)、当时,求y与x的关系式(不要求写出自变量x的取值范围);(2)、当时,球能否越过球网?球会不会出界?请说明理由;(3)、若球一定能越过球网,又不出边界,求h的取值范围.23. 在平面直角坐标系中,某个函数图象上任意两点的坐标分别为和(其中t为常数且),将的部分沿直线翻折,翻折后的图象记为;将的部分沿直线翻折,翻折后的图象记为 , 将和及原函数图象剩余的部分组成新的图象G.例如:如图,当时,原函数 , 图象G所对应的函数关系式为.
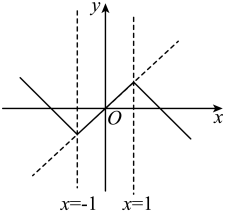 (1)、当时,原函数为 , 图象G与坐标轴的交点坐标是.(2)、对应函数(n为常数).
(1)、当时,原函数为 , 图象G与坐标轴的交点坐标是.(2)、对应函数(n为常数).①时,若图象G与直线恰好有两个交点,求t的取值范围.
②当时,若图象G在上的函数值y随x的增大而减小,直接写出n的取值范围.
24. 如图,在中, , .点D是直线上一动点.过点D作 , 满足点E在上方, , 以、为邻边作.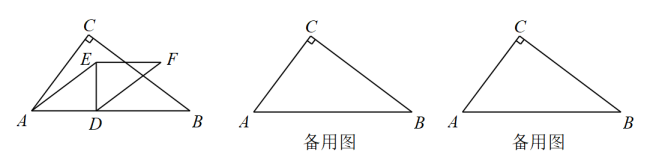 (1)、求的长以及点C到的距离;(2)、设线段与边交于点M,线段与边交于点N.当时,求的长;(3)、连接 , 沿直线分割 , 当分割的两部分可以拼成一个不重叠无缝隙的三角形时,求的长.
(1)、求的长以及点C到的距离;(2)、设线段与边交于点M,线段与边交于点N.当时,求的长;(3)、连接 , 沿直线分割 , 当分割的两部分可以拼成一个不重叠无缝隙的三角形时,求的长.