浙江省金华市金东区2023年初中毕业升学适应性检测数学试题

试卷更新日期：2023-04-18 类型：中考模拟

进入出卷网下载

一、单选题

1. 实数2023的绝对值等于（）

A、2023 B、 $- 2023$ C、 $\pm 2023$ D、 $\frac{1}{2023}$

查看试题解析
2. 化简 $\frac{m + n}{2 m - n} + \frac{m - n}{2 m - n}$ 的结果是（）

A、 $\frac{2 m}{2 m - n}$ B、0 C、2 D、 $\frac{2 n}{2 m - n}$

查看试题解析
3. 近年来，金东区积极构建消费和谐关系，促进消费维权协同共治，助力经济平稳健康发展.过去一年，金东区加大处置投诉举报案件的力度，为消费者挽回经济损失4790000元.其中数字4790000用科学记数法可表示为（）

A、 $479 \times 1 0^{4}$ B、 $4.79 \times 1 0^{5}$ C、 $47.9 \times 1 0^{5}$ D、 $4.79 \times 1 0^{6}$

查看试题解析
4. 垃圾分类一小步，低碳生活一大步，垃圾桶上常有以下四种垃圾分类标识的图案，下列图案既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 一元二次方程 $x^{2} + x - 1 = 0$ 根的情况是（）

A、有一个实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、没有实数根

查看试题解析
6. 在如图所示的几何体中，主视图和俯视图相同的是（）

A、正方体 B、三棱柱 C、圆柱 D、圆锥

查看试题解析
7. 如图，线段 $B D ， C E$ 相交于点A， $D E ∥ B C$ .若 $B C = 3 ， D E = 1.5 ， A D = 2$ ，则 $B D$ 的长为（）

A、3 B、4 C、5 D、6

查看试题解析
8. 如图，在 $4 \times 4$ 的方格中（共有16个小方格），每个小方格都是边长为1的正方形，O，A，B分别是小正方形的顶点，则扇形 $O A B$ 的面积等于（）

A、 $2 π$ B、 $\sqrt{2} π$ C、 $2 \sqrt{2} π$ D、 $\frac{\sqrt{2}}{2} π$

查看试题解析
9. 某市举行中学生党史知识竞赛，如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率（该校优秀人数与该校参加竞赛人数的比值）y与该校参加竞赛人数x的情况，其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上，则这四所学校在这次党史知识竞赛中成绩优秀人数最多的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
10. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 3$ ，以 $A B$ 为一边向三角形外作正方形 $A B E F$ ，正方形对角线的交点为O，且 $O C = 4 \sqrt{2}$ ，那么 $B C$ 的长等于（）

A、 $3 \sqrt{2}$ B、5 C、 $2 \sqrt{5}$ D、 $\frac{9}{2}$

查看试题解析

二、填空题

11. 二次根式 $\sqrt{2 m - 1}$ 中，字母m的取值范围是 .

查看试题解析
12. 分解因式： $4 x^{2} y - 12 x y =$ .

查看试题解析
13. 如图， $A B$ 是 $⊙ O$ 的直径，点D在 $A B$ 的延长线上， $D C$ 切 $⊙ O$ 于点C，若 $∠ D = 36 °$ ，则 $∠ A$ 的度数为.

查看试题解析
14. 现有四张正面分别标有数字 $- 4$ ， $- 2$ ， 1，3的卡片，它们除数字不同外，其余完全相同.将卡片背面朝上洗匀后，从中随机取出一张，再从剩下的卡片中随机取出一张.则两次取出卡片上的数字之和为正数的概率为.

查看试题解析
15. 如图，正方形 $O A_{1} B_{1} C_{1}$ ， $C_{1} A_{2} B_{2} C_{2}$ ， $C_{2} A_{3} B_{3} C_{3}$ ， …的顶点 $A_{1} ， A_{2} ， A_{3}$ ， …在直线 $y = k x + b$ 上，顶点 $C_{1}$ ， $C_{2}$ ， $C_{3}$ ， …在x轴上，已知 $B_{1} (1 ， 1)$ ， $B_{2} (3 ， 2)$ ，那么点 $A_{8}$ 的坐标为.

查看试题解析
16. 如图1为某小区出入口栅栏道闸， $B E ， C F$ 为栅栏道闸的转动杆，上面有10根等间距的竖杆，未抬起时与地面保持水平，竖杆竖直地面，在道闸抬起时最大旋转角度为 $70 °$ ， $M N$ 为门墙， $B E = C F = 3.1 m$ ， $A D = 1.2 m$ ， $A B = C D = 0.2 m$ ，转动杆外端E，F距离杆 $G H$ 与门墙 $M N$ 均为 $0.1 m$ ，左侧9根竖杆底部离地面均为 $0.1 m$ .（ $s i n 70 ° \approx 0.94$ ， $c o s 70 ° \approx 0.34$ ， $t a n 70 ° \approx 2.75$ ）

(1)、如图2，当道闸转动 $30 °$ 抬起时，第五根竖杆的底端P到地面的距离为.

(2)、现有一辆货车进小区装货，已知货车宽 $2.2 m$ ，货车进出需保持与门墙 $0.2 m$ 的安全距离，该货车安全进出小区的离地高度不得超过m.

查看试题解析

三、解答题

17. 计算： $t a n 60 ° - | - \sqrt{3} | + {(\sqrt{5} - 1)}^{0} + {(\frac{1}{2})}^{- 2}$ ．

查看试题解析
18. 解不等式： $5 x - 1 \leq 3 (x + 1)$

查看试题解析
19. 如图，一次函数 $y = k_{1} x + 8$ 与反比例函数 $y = \frac{k_{2}}{x} (x > 0)$ 的图象交于 $A (1 ， 6)$ ， $B (3 ， n)$ 两点.

(1)、求反比例函数的解析式和n的值；

(2)、根据图象直接写出不等式 $k_{1} x + 8 < \frac{k_{2}}{x}$ 的解集.

查看试题解析
20. 我国男性的体质系数计算公式是： $m = \frac{w}{H - 105} \times 100 %$ ，其中w表示体重（单位： $k g$ ），H表示身高（单位： $c m$ ），通过计算出的体质系数m对体质进行评价，天元区在某中学九年级学生中随机抽取n名男生进行体质评价，评价结果统计如下：
m
$< 80 %$
$80 % ∼ 90 %$
$90 % ∼ 110 %$
$110 % ∼ 120 %$
$> 120 %$
评价结果
明显消瘦
消瘦
正常
过重
肥胖
结果占比
$5 %$
b
c
$40 %$
d

(1)、已知某男生的身高是 $170 c m$ ，体重是 $75 k g$ ，求他的体质评价结果；

(2)、求：①n的值；②a、d的值；

(3)、若该校九年级共有男生 $400$ 人，试估计该校九年级体质评价结果为“消瘦”和“正常”的男生人数和.

查看试题解析
21. 如图，在四边形ABCD中，AB=AD，CB=CD，对角线AC、BD交于点O，过点B作BE∥CD交AC于点E.

(1)、求证；四边形BCDE是菱形；

(2)、若AB=5，E为AC的中点，当BC的长为时，四边形BCDE是正方形.

查看试题解析
22. 如图， $A B$ 为 $⊙ O$ 的直径， $C D$ 为弦，且 $C D ⊥ A B$ 于E，F为 $B A$ 延长线上一点， $C A$ 恰好平分 $∠ F C E$ .

(1)、求证： $F C$ 与 $⊙ O$ 相切；

(2)、连接 $O D$ ，若 $O D ∥ A C$ ，求 $\frac{A F}{A B}$ 的值.

查看试题解析
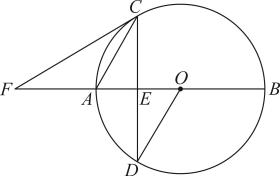23. 如图1，已知排球场的长度为 $18 m$ ，宽 $9 m$ ，位于球场中线处的球网 $A B$ 的高度为 $2.24 m$ .一球员定点发球技术非常稳定，当他站在底线中点O处发球时，排球运动轨迹是如图2的抛物线，C点为击球点， $O C = 1.8 m$ ，球飞行到达最高点F处时，其高度为 $2.6 m$ ， F与C的水平之距为 $6 m$ ，以O为原点建立如图所示的平面直角坐标系（排球大小忽略不计）.

(1)、当他站在底线中点O处向正前方发球时，
①求排球飞行的高度y与水平距离x之间的函数关系式（不用写x的取值范围）.
②这次所发的球能够过网吗？如果能够过网，是否会出界？并说明理由.

(2)、假设该球员改变发球方向和击球点高度时球运动轨迹的抛物线形状不变，在点O处上方击球，要使球落在①号区域（以对方场地的边线底线交点M为圆心，半径为 $1.5 m$ 的扇形）内，球员跳起的高度范围是多少？（ $\sqrt{17} \approx 4.12$ ，结果保留两位小数）

查看试题解析
24. 如图，在 $△ A B C$ 中， $A B = A C = 5$ ， $B C = 6$ ，点P是射线 $B C$ 上的动点，连结 $A P$ ，在 $A P$ 的右边作 $∠ P A Q = \frac{1}{2} ∠ B A C$ ，交射线 $B C$ 于点Q.

(1)、当 $B P = 1$ 时，求点P到 $A B$ 的距离.

(2)、当点P在线段 $B C$ 上运动时，记 $B P = x$ ， $C Q = y$ ，求y关于x的函数表达式和自变量x的取值范围.

(3)、在点P的运动过程中，不再连结其他线段，当图中存在某个角为45°时，求 $B Q$ 的长，并指出相应的45°角.

查看试题解析

m	$< 80 %$	$80 % ∼ 90 %$	$90 % ∼ 110 %$	$110 % ∼ 120 %$	$> 120 %$
评价结果	明显消瘦	消瘦	正常	过重	肥胖
结果占比	$5 %$	b	c	$40 %$	d