浙江省金华市2023年中考一模数学试题

试卷更新日期：2023-04-18 类型：中考模拟

进入出卷网下载

一、单选题

1. 2022的相反数是（）

A、 $\frac{1}{2022}$ B、 $- \frac{1}{2022}$ C、 $2022$ D、 $- 2022$

查看试题解析
2. 下列运算正确的是（）

A、 $2 x + y = 2 x y$ B、 $x^{2} \cdot x^{3} = x^{6}$ C、 $2 x^{6} \div x^{2} = 2 x^{4}$ D、 $4 x - 5 x = - 1$

查看试题解析
3. 某中学篮球队12名队员的年龄情况如下表，则这个队队员年龄的众数和中位数分别（）

年龄（岁）

14

15

16

17

18

人数（人）

1

4

3

2

2

A、15，16 B、15，15 C、15，15.5 D、16，15

查看试题解析
4. 国家卫健委网站消息：截至2022年5月27日，31个省（自治区，直辖市）和新疆生产建设兵团累计报告接种新冠病毒疫苗超过33亿剂次，用科学记数法表示33亿是（）

A、 $3.3 \times 1 0^{8}$ B、 $33 \times 1 0^{8}$ C、 $3.3 \times 1 0^{9}$ D、 $3.3 \times 1 0^{10}$

查看试题解析
5. 已知 $∠ α = 76 ° 2 2^{'}$ ，则 $∠ α$ 的补角是（）.

A、 $103 ° 3 8^{'}$ B、 $103 ° 7 8^{'}$ C、 $13 ° 3 8^{'}$ D、 $13 ° 7 8^{'}$

查看试题解析
6. 已知一个底面半径为 $3 c m$ 的圆锥，它的母线长是 $5 c m$ ，则这个圆锥的侧面积是（） $c m^{2}$

A、 $15 π$ B、 $45 π$ C、 $30 π$ D、 $20 π$

查看试题解析
7. 北京2022冬奥会吉样物“冰墩墩”和“雪容融”受到大家的喜爱，某网店出售这两种吉祥物礼品，借价如图所示.小明妈妈一共买10件礼品，总共花费不超过900元，如果设购买冰墩墩礼品 $x$ 件，则能够得到的不等式是（）

A、 $100 x + 80 (10 - x) > 900$ B、 $100 x + 80 (10 - x) < 900$ C、 $100 x + 80 (10 - x) \geq 900$ D、 $100 x + 80 (10 - x) \leq 900$

查看试题解析
8. 在数轴上，点A所表示的实数为4，点B所表示的实数为b， $⊙ A$ 的半径为2，要使点B在 $⊙ A$ 内时，实数b的取值范围是（）

A、 $b > 2$ B、 $b > 6$ C、 $b < 2$ 或 $b > 6$ D、 $2 < b < 6$

查看试题解析
9. 如图，在Rt $△ A B C$ 中， $∠ C ＝ 9 0^{∘} ， ∠ A ＝ 3 0^{∘} ， E$ 为 $A B$ 上一点且 $A E ＝ 4 E B ， E F ⊥ A C$ 于 $F$ ，连结 $F B$ ，则 $t a n ∠ C F B =$ （）

A、 $5 \sqrt{3}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{2 \sqrt{3}}{3}$ D、 $\frac{5 \sqrt{3}}{3}$

查看试题解析
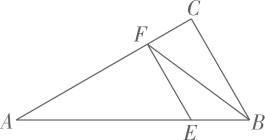10. 矩形纸片 $A B C D$ 中， $B C = 2 A B$ ，将纸片对折，使顶点A与顶点C重合，得折痕 $E F$ ，将纸片展开铺平后再进行折叠，使顶点B与顶点D重合，得折痕 $M N$ ，展开铺平后如图所示.若折痕 $E F$ 与 $M N$ 较小的夹角记为 $θ$ ，则 $s i n θ =$ （）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{2 \sqrt{5}}{5}$ D、 $\frac{\sqrt{5}}{5}$

查看试题解析

二、填空题

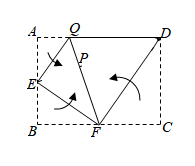
11. 若分式 $\frac{x}{x + 3}$ 有意义，则x的取值范围是.

查看试题解析
12. 从﹣3，﹣l，π，0，3这五个数中随机抽取一个数，恰好是负数的概率是.

查看试题解析
13. 一元二次方程x²+bx+2021＝0的一个根为x＝﹣1，则b的值为.

查看试题解析
14. 如图，在矩形ABCD中，E，F分别是边AB，BC上的点.将∠A，∠B，∠C按如图所示的方式向内翻折，EQ，EF，DF为折痕.若A，B，C恰好都落在同一点P上，AE＝1，则ED＝.

查看试题解析
15. 如图，在矩形ABCD中，AB＝4，BC＝3，将△BCD沿射线BD平移长度a（a＞0）得到△B'C'D'，连接AB'，AD'，则当△AB'D'是直角三角形时，a的长为 .

查看试题解析
16. 如图是一个矩形足球球场， $A B$ 为球门， $C D ⊥ A B$ 于点D， $A B = a$ 米.某球员沿 $C D$ 带球向球门 $A B$ 进攻，在Q处准备射门.已知 $B D = 3 a$ 米， $Q D = 3 a$ 米，则 $t a n ∠ A Q B =$ ；已知对方门将伸开双臂后，可成功防守的范围大约为 $0.5 a$ 米；此时门将站在张角 $∠ A Q B$ 内，双臂伸开 $M N$ 且垂直于 $A Q$ 进行防守， $M N$ 中点与 $A B$ 距离米时，刚好能成功防守.

查看试题解析

三、解答题

17. 计算： $\sqrt{12} - 2 s i n 60 ° + | 1 - \sqrt{3} | + 202 2^{0}$ .

查看试题解析
18. 如图是由小正方形组成的 $6 \times 6$ 的网格， $△ A B C$ 的三个顶点A、B、C均在格点上，请按要求在给定的网格中，仅用无刻度的直尺，分别按下列要求作图，保留作图痕迹，不写画法.

(1)、在图1中的 $A B$ 上画出 $△ A B C$ 的高线；

(2)、在图2中的 $A C$ 上找出一点E，画线段 $B E$ ，使 $△ A B E$ 与 $△ C B E$ 面积比为 $3 ： 7$ 两部分；

(3)、在图3中的 $B C$ 上找一点F，画 $∠ B A F$ ，使得 $∠ C = 2 ∠ B A F$ .

查看试题解析
19. 为响应上级“双减”号召，某校开设了阅读、运动、娱乐、其他等四个方面的课后延学活动.下面是随机抽取的部分同学参加活动的统计情况，请你根据图中提供的信息解答下列问题：

(1)、本次调查了人.

(2)、补全折线统计图，并求出扇形统计图中“其他”所对的圆心角度数.

(3)、若该校共有2400名学生，试估算参加“阅读”方面活动的共有多少人.

查看试题解析
20. 图1是新冠疫情期间测温员用“额温枪”对居民李阿姨测温时的手绘图，图2是其侧面示意图，其中枪柄 $C D$ 和手臂 $B C$ 始终在同一条直线上，额头为F，枪身 $D E$ 与身体 $F Q$ 保持垂直，量得胳膊 $A B = 24 c m ， B D = 40 c m$ ，肘关节B与枪身端点E之间的水平宽度为 $28 c m$ （即 $B H$ 的长度），枪身 $D E = 8 c m$ .

(1)、求 $∠ D B H$ 的度数.

(2)、根据疫情防控相关操作要求，规定测温时枪身端点E与额头F之间的距离需在 $3 c m$ 到 $5 c m$ 之间.若 $∠ A B C = 75 °$ ，李阿姨与测温员之间的距离为 $48 c m$ .求此时枪身端点E与李阿姨额头F之间的距离，并判断测温枪与额头之间的距离是否在规定范围内，说明相应理由.（结果保留小数点后两位，参考数据： $\sqrt{2} \approx 1.414 ， \sqrt{3} \approx 1.732$ ）

查看试题解析
21. 如图，已知AB是 $⊙ O$ 的直径， $△ A B D$ 为 $⊙ O$ 的内接三角形，C为BA延长线上一点，连接CD， $O F ⊥ A D$ 于点E，交CD于点F， $∠ A D C = ∠ A O F$ .

(1)、求证：CD是 $⊙ O$ 的切线.

(2)、若 $s i n C = \frac{1}{2} ， B D = 2 \sqrt{3}$ ，求 $\overset{⌢}{A D}$ 的长.

查看试题解析
22. 如图，抛物线 $y = a x^{2} + b x + 3$ 与x轴相交于点 $A (1 ， 0) ， B (3 ， 0)$ ，与y轴相交于点C.

(1)、求抛物线的解析式.

(2)、点 $M (x_{1} ， y_{1}) ， N (x_{2} ， y_{2})$ 是抛物线上不同的两点.
①若 $y_{1} = y_{2}$ ，求 $x_{1} ， x_{2}$ 之间的数量关系.
②若 $x_{1} + x_{2} = 2 (x_{1} - x_{2})$ ，求 $y_{1} - y_{2}$ 的最小值.

查看试题解析
23. 如图1，在平面直角坐标系中，四边形AOBC为矩形，BC= $2 \sqrt{3}$ ， ∠BOC=60°，D为BC中点.某反比例函数过点D，且与直线OC交于点E.

(1)、点E的坐标为.

(2)、好奇的小明在探索一个新函数.若点P为x轴上一点，过点P作x轴的垂线交直线AC于点Q，交该反比例函数图象于点R.若y′=PQ+PR，点P横坐标为x. $y^{'}$ 关于x的图像如图2，其中图像最低点F、G横坐标分别为（ $\sqrt{2}$ ， $\sqrt{2}$ ）、（ $- \sqrt{2}$ ， $- \sqrt{2}$ ）.
①求 $y^{'}$ 与x之间的函数关系式.
②写出该函数的两条性质.

(3)、已知1<x<4
①若关于x的方程x²－4x－m=0有解，求m的取值范围.小明思考过程如下：由x²－4x－m=0得m=x²－4x，m是关于x的二次函数，根据x的范围可以求出m的取值范围.请你完成解题过程.
②若关于x的方程 $\sqrt{6} x^{2} - m x + 2 \sqrt{6} = 0$ 有解，请直接写出m的取值范围.

查看试题解析
24. 如图1，在平面直角坐标系中，点O为坐标原点，点A的坐标为 $(- 8 ， 0)$ ，直线 $B C$ 经过点 $B (- 8 ， 4)$ 、 $C (0 ， 4)$ .将四边形 $O A B C$ 绕点O按顺时针方向旋转α度得到四边形 $O A^{'} B^{'} C^{'}$ ，此时直线 $O A^{^{'}}$ 、直线 $B^{^{'}} C^{^{'}}$ 分别与直线 $B C$ 相交于点P、Q.

(1)、四边形 $O A B C$ 的形状是，当 $α = 90 °$ 时， $\frac{B P}{P Q}$ 的值是；

(2)、①如图2，当四边形 $O A^{'} B^{'} C^{'}$ 的顶点 $B^{'}$ 落在y轴正半轴上时，求 $\frac{B P}{P Q}$ 的值；
②如图3，当四边形 $O A^{'} B^{'} C^{'}$ 的顶点 $B^{'}$ 落在直线 $B C$ 上时，求 $△ O P B^{'}$ 的面积；

(3)、在四边形 $O A B C$ 旋转过程中，当 $0 ° < α \leq 180 °$ 时，是否存在这样的点P和点Q，使得 $B P = \frac{1}{2} B Q$ ，若存在，请直接写出点P的坐标；若不存在，请说明理由.

查看试题解析

年龄（岁）	14	15	16	17	18
人数（人）	1	4	3	2	2