浙江省湖州市南浔区2023年中考一模数学试题
试卷更新日期:2023-04-18 类型:中考模拟
一、单选题
-
1. 3的相反数是( ).A、 B、3 C、 D、2. 下列图案是历届冬奥会会徽,其中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 截止2023年2月,全国学习强国注册用户总数超过257000000人,数257000000用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 在我县“我的中国梦”演讲比赛中,有7名同学参加了比赛,他们最终决赛的成绩各不相同.其中一名学生想要知道自己是否进入前3名,不仅要知道自己的分数,还得知道这7名学生成绩的( )A、众数 B、方差 C、平均数 D、中位数6. 通过如下尺规作图,能确定点D是BC边中点的是( )A、
3. 截止2023年2月,全国学习强国注册用户总数超过257000000人,数257000000用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 在我县“我的中国梦”演讲比赛中,有7名同学参加了比赛,他们最终决赛的成绩各不相同.其中一名学生想要知道自己是否进入前3名,不仅要知道自己的分数,还得知道这7名学生成绩的( )A、众数 B、方差 C、平均数 D、中位数6. 通过如下尺规作图,能确定点D是BC边中点的是( )A、 B、
B、 C、
C、 D、
D、 7. 若 , 则下列各式中正确的是( )A、 B、 C、 D、8. 我国古代数学著作《孙子算经》有“多人共车”问题:“今有三人共车,二车空;二人共车,九人步,问:人与车各几何?”其大意如下:有若干人要坐车,如果每3人坐一辆车,那么有2辆空车;如果每2人坐一辆车,那么有9人需要步行,问人与车各多少?设共有x人,y辆车,则可列方程组为( )A、 B、 C、 D、9. 甲,乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑电动车,甲到达B地停留半个小时后返回A地,如图是他们离A地的距离y(千米)与经过时间x(小时)之间的函数关系图象.当甲与乙相遇时距离A地( )
7. 若 , 则下列各式中正确的是( )A、 B、 C、 D、8. 我国古代数学著作《孙子算经》有“多人共车”问题:“今有三人共车,二车空;二人共车,九人步,问:人与车各几何?”其大意如下:有若干人要坐车,如果每3人坐一辆车,那么有2辆空车;如果每2人坐一辆车,那么有9人需要步行,问人与车各多少?设共有x人,y辆车,则可列方程组为( )A、 B、 C、 D、9. 甲,乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑电动车,甲到达B地停留半个小时后返回A地,如图是他们离A地的距离y(千米)与经过时间x(小时)之间的函数关系图象.当甲与乙相遇时距离A地( ) A、16千米 B、18千米 C、72千米 D、74千米10. 如图,点P是斜边AB上的动点,点D、E分别在AC、BC边上,连结PD、PE,若 , , , , 则当取得最小值时AP的长是( )
A、16千米 B、18千米 C、72千米 D、74千米10. 如图,点P是斜边AB上的动点,点D、E分别在AC、BC边上,连结PD、PE,若 , , , , 则当取得最小值时AP的长是( ) A、18 B、 C、 D、
A、18 B、 C、 D、二、填空题
-
11. 计算.12. 为减少安全隐患,某学校将一批方角型书桌更换为圆角型书桌.已知此书桌桌角所在圆的半径为5cm,所对的圆心角为90°,则一个桌角的弧长为cm.13. 从一盒写有“鲜肉1只,蛋黄2只”的端午粽子(所有粽子的形状大小都一样)礼盒中,随机取出2只粽子,恰好都是蛋黄粽子的概率是.14. 一根排水管的截面如图所示,已知排水管的半径OB=5cm,水面宽AB=8,则截面圆心O到水面的距离OC的长是.
 15. 如图,在中, , , , D为边上一点,沿将三角形进行折叠,使点A落在点E处,记与边的交点为F,若 , 则的长为.
15. 如图,在中, , , , D为边上一点,沿将三角形进行折叠,使点A落在点E处,记与边的交点为F,若 , 则的长为. 16. 将一副三角板按如图方式放置在平面直角坐标系中,已知AB=2,反比例函数的图象恰好经过顶点C,D,轴,则k的值为.
16. 将一副三角板按如图方式放置在平面直角坐标系中,已知AB=2,反比例函数的图象恰好经过顶点C,D,轴,则k的值为.
三、解答题
-
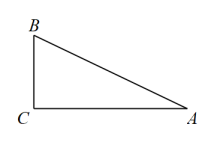
17. 计算:18. 如图,已知在中, , , , 求的长和的值
 19. 小王和小凌在解答“解分式方程: ”的过程如下框,请你判断他们的解法是否正确?若错误,请写出你的解答过程.
19. 小王和小凌在解答“解分式方程: ”的过程如下框,请你判断他们的解法是否正确?若错误,请写出你的解答过程.小王的解法:
解,去分母得: ①
去括号得: ②
移项得: ③
合并同类项得: ④
系数化为1得: ⑤
是原分式方程的解 ⑥
小凌的解法:
解,去分母得: ①
移项得: ②
合并同类项得: ③
系数化为1得: ④
是原分式方程的解 ⑤
20. 劳动教育是学校贯彻“五育并举”的重要举措,某校倡议学生在家帮助父母做一些力所能及的家务,小杨随机抽取该校部分学生进行问卷调查,问卷调查表如下所示,并根据调查结果绘制了两幅不完整的统计图.平均每周做家务的时间调查表
设平均每周做家务的时间为x小时,则最符合你的选项是( )(单选)
A. B. C. D.
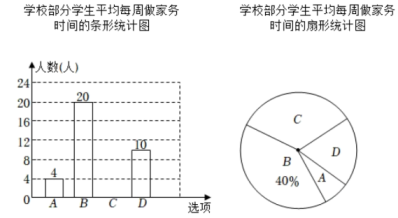
根据统计图中的信息,解答下列问题:
(1)、求小杨共调查了多少人和扇形统计图中表示选项“D”的扇形的圆心角度数;(2)、将条形统计图补充完整;(3)、该校有1500名学生,根据抽样调查结果,请你估计该校平均每周做家务的时间不少于2小时的学生人数.21. 如图,在中, , D为上的一点,以为直径的半圆与交于点F,且切于点E. (1)、求证:;(2)、若 , , 求的长.22. 某校的甲,乙两位老师同住一小区,该小区与学校相距1800米.甲从小区步行去学校,出发10分钟后乙再出发,乙从小区先骑公共自行车,途经学校又骑行若干米到达还车点后,立即以45米/分钟的速度步行到学校,设甲步行的时间为x(分钟),图中线段 和折线 分别表示甲,乙离开小区的路程y米)与甲步行时间x(分钟)的函数关系的图象,根据图中所给信息,解答下列问题:
(1)、求证:;(2)、若 , , 求的长.22. 某校的甲,乙两位老师同住一小区,该小区与学校相距1800米.甲从小区步行去学校,出发10分钟后乙再出发,乙从小区先骑公共自行车,途经学校又骑行若干米到达还车点后,立即以45米/分钟的速度步行到学校,设甲步行的时间为x(分钟),图中线段 和折线 分别表示甲,乙离开小区的路程y米)与甲步行时间x(分钟)的函数关系的图象,根据图中所给信息,解答下列问题: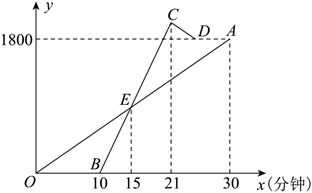 (1)、写出点E横坐标的实际意义,并求出点E的纵坐标.(2)、求乙从还车点到学校所花的时间.(3)、两人何时相距300米?23. 单板滑雪大跳台是北京冬奥会比赛项目之一,滑雪大跳台在设计时融入了敦煌壁画中“飞天”的元素,故又名“雪飞天”.图1为“雪飞天”滑雪大跳台赛道的横截面示意图.运动员从D点起跳后到着陆坡着落时的飞行路线可以看作是抛物线的一部分,取水平线为x轴,铅垂线为y轴,建立平面直角坐标示如图2,从起跳到着落的过程中,运动员的铅垂高度y(单位:m)与水平距离x(单位:m)近似满足函数关系.在着陆坡上设置点作为标准点,着陆点在K点或超过K点视为成绩达标.
(1)、写出点E横坐标的实际意义,并求出点E的纵坐标.(2)、求乙从还车点到学校所花的时间.(3)、两人何时相距300米?23. 单板滑雪大跳台是北京冬奥会比赛项目之一,滑雪大跳台在设计时融入了敦煌壁画中“飞天”的元素,故又名“雪飞天”.图1为“雪飞天”滑雪大跳台赛道的横截面示意图.运动员从D点起跳后到着陆坡着落时的飞行路线可以看作是抛物线的一部分,取水平线为x轴,铅垂线为y轴,建立平面直角坐标示如图2,从起跳到着落的过程中,运动员的铅垂高度y(单位:m)与水平距离x(单位:m)近似满足函数关系.在着陆坡上设置点作为标准点,着陆点在K点或超过K点视为成绩达标.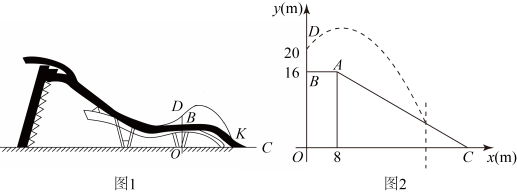
水平距离x(m)
0
2
6
10
14
18
铅垂高度y(m)
(1)、在某运动员的一次试跳中,测得该运动员的水平距离x与铅垂高度y的几组数据如上表,根据上述数据,直接写出该运动员铅垂高度的最大值,并求出满足的函数关系式(2)、请问在此次试跳中,该运动员的成绩是否达标?(3)、此次试跳中,该运动员在空中从起跳到达最高点的高度或从最高点到下落的高度h(m)与时间t(s)均满足(其中g为常数,表示重力加速度,取),运动员要完成“飞天”动作至少在空中要停留3秒钟,问该运动员从起跳到落地能完成动作吗?24. 如图,在矩形ABCD中,AE平分∠BAD交射线BC于点E,过点C作CF⊥AE交射线AE于点F,连结BD交AE于点G,连结DF交射线BC于点H. (1)、当AB<AD时,
(1)、当AB<AD时,①求证:BE=CD,
②猜想∠BDF的度数,并说明理由.
(2)、若时,求tan∠CDF的值(用含k的代数式表示).