广西壮族自治区柳州市2023年九年级初中学业水平考试数学模拟试题
试卷更新日期:2023-04-18 类型:中考模拟
一、单选题
-
1. 有理数3,1,﹣2,4中,小于0的数是( )A、3 B、1 C、﹣2 D、42. 北京的故宫是中国明清两代的皇家宫殿,旧称紫禁城,位于北京中轴线中心,占地面积约班别为720000平方米.数据720000用科学记数法表示为( )A、 B、 C、 D、3. 把不等式的解集在数轴上表示出来,正确的是( )A、
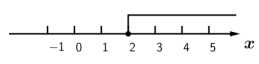 B、
B、 C、
C、 D、
D、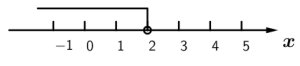 4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,若 , , 则∠1的度数为( )
4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,若 , , 则∠1的度数为( )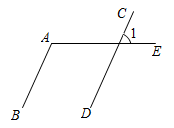 A、110° B、100° C、80° D、70°6. 某班5名同学参加学校“感党恩,跟党走”主题演讲比赛,他们的成绩(单位:分)分别是80,60,80,70,90,这组数据的中位数是( )A、60 B、70 C、80 D、907. 如图①所示,有6张写有汉字的卡片,它们的背面都相同,现将它们背面朝上洗匀后如图2摆放,从中任意翻开一张是汉字“信”的概率是( )
A、110° B、100° C、80° D、70°6. 某班5名同学参加学校“感党恩,跟党走”主题演讲比赛,他们的成绩(单位:分)分别是80,60,80,70,90,这组数据的中位数是( )A、60 B、70 C、80 D、907. 如图①所示,有6张写有汉字的卡片,它们的背面都相同,现将它们背面朝上洗匀后如图2摆放,从中任意翻开一张是汉字“信”的概率是( )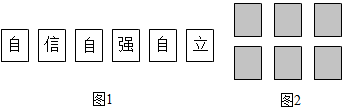 A、 B、 C、 D、8. 正八边形的每个内角的度数是( )A、144° B、140° C、135° D、120°9. 如图,A , B , C是⊙O上的三点,若 ,则 的度数是( )
A、 B、 C、 D、8. 正八边形的每个内角的度数是( )A、144° B、140° C、135° D、120°9. 如图,A , B , C是⊙O上的三点,若 ,则 的度数是( ) A、40° B、35° C、30° D、25°10. 如图,某商场一楼与二楼之间的电梯示意图.∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( )
A、40° B、35° C、30° D、25°10. 如图,某商场一楼与二楼之间的电梯示意图.∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( )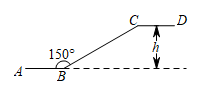 A、m B、m C、8m D、4m11. 筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2,已知圆心O在水面上方,且 被水面截得的弦 长为6米, 半径长为4米.若点C为运行轨道的最低点,则点C到弦 所在直线的距离是( )
A、m B、m C、8m D、4m11. 筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2,已知圆心O在水面上方,且 被水面截得的弦 长为6米, 半径长为4米.若点C为运行轨道的最低点,则点C到弦 所在直线的距离是( )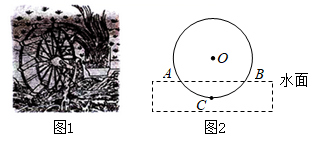 A、1米 B、 米 C、2米 D、 米12. 如图,在平面直角坐标系中,已知 , , , M是线段上的一个动点,连接 , 过点M作交y轴于点N.若点M,N在直线上,则b的最大值是( )
A、1米 B、 米 C、2米 D、 米12. 如图,在平面直角坐标系中,已知 , , , M是线段上的一个动点,连接 , 过点M作交y轴于点N.若点M,N在直线上,则b的最大值是( )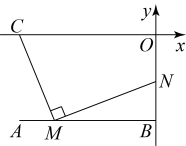 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 若二次根式在实数范围内有意义,则x的取值范围是 .14. 小丽的笔试成绩为100分,面试成绩为90分,若笔试成绩、面试成绩按6:4计算平均成绩,则小丽的平均成绩是分.15. 点P(m,2)在第二象限内,则m的值可以是(写出一个即可).16. 分解因式:x2﹣4x= .
17. 如图,在中,P,Q分别为 , 的中点.若的面积 , 则的面积.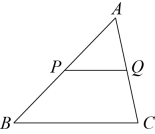 18. 如图1,在矩形ABCD中, , 对角线AC,BD相交于点O,动点P由点A出发,沿向点D运动.设点P的运动路程为x,的面积为y,y与x的函数关系图象如图2所示,则AD边的长为.
18. 如图1,在矩形ABCD中, , 对角线AC,BD相交于点O,动点P由点A出发,沿向点D运动.设点P的运动路程为x,的面积为y,y与x的函数关系图象如图2所示,则AD边的长为.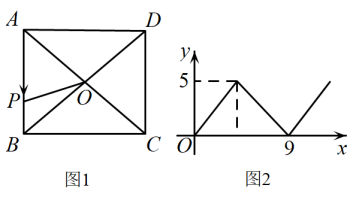
三、解答题
-
19. 计算:.20. 解方程:.21. 如图,在平面直角坐标系中, 的三个顶点分别是A(1,3),B(4,4),C(2,1).
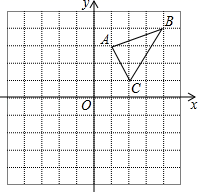
( 1 )把 向左平移4个单位后得到对应的 A1B1C1 , 请画出平移后的 A1B1C1;
( 2 )把 绕原点O旋转180°后得到对应的 A2B2C2 , 请画出旋转后的 A2B2C2;
( 3 )观察图形可知, A1B1C1与 A2B2C2关于点( , )中心对称.
22. 某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图. (1)、这次被调查的同学共有名;(2)、把条形统计图补充完整;(3)、校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校18 000名学生一餐浪费的食物可供多少人食用一餐?23. 某中学为丰富学生的校园生活,准备一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需170元,购买2个足球和5个篮球共需260元.(1)、足球、篮球的单价分别是多少元?(2)、根据该中学的实际情况,需一次性购买足球和篮球共46个,要求购买足球和篮球的总费用不超过1480元,这所中学最多可以购买多少个篮球?24. 综合与实践
(1)、这次被调查的同学共有名;(2)、把条形统计图补充完整;(3)、校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校18 000名学生一餐浪费的食物可供多少人食用一餐?23. 某中学为丰富学生的校园生活,准备一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需170元,购买2个足球和5个篮球共需260元.(1)、足球、篮球的单价分别是多少元?(2)、根据该中学的实际情况,需一次性购买足球和篮球共46个,要求购买足球和篮球的总费用不超过1480元,这所中学最多可以购买多少个篮球?24. 综合与实践小明遇到这样一个问题,如图1,中, , , 点D为的中点,求的取值范围.
小明发现老师讲过的“倍长中线法”可以解决这个问题,所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法,他的做法是:如图2,延长到E,使 , 连接 , 构造 , 经过推理和计算使问题得到解决
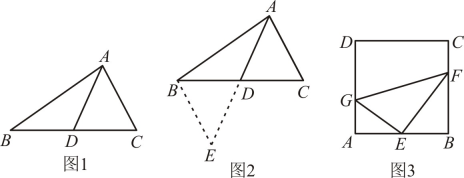
请回答:
(1)、小明证明用到的判定定理是:____;(填入你选择的选项字母)A、 B、 C、 D、(2)、的取值范围是.(3)、小明还发现:倍长中线法最重要的一点就是延长中线一倍,完成全等三角形模型的构造.
参考小明思考问题的方法,解决问题:
如图3,在正方形中,E为边的中点,G、F分别为 , 边上的点,若 , , , 求的长.25. 如图,是的直径,点C是上一点,和过点C的切线互相垂直,垂足为D,直线与的延长线相交于P.弦平分 , 交直径于点F,连接. (1)、求证:平分;(2)、若 , , 求的长.26. 如图,抛物线与x轴交于 , 两点,与y轴交于点C,点D是抛物线的顶点.
(1)、求证:平分;(2)、若 , , 求的长.26. 如图,抛物线与x轴交于 , 两点,与y轴交于点C,点D是抛物线的顶点.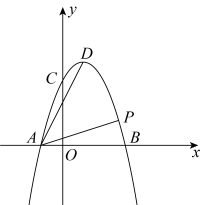 (1)、求抛物线解析式;(2)、求开口向下的二次函数的最大值时采用的步骤是:第一,求出二次函数的顶点坐标;第二,确定自变量x的取值范围;第三判定是否在其范围内,若在,则最大值是顶点纵坐标,若不在,要根据其增减性求最大值,即当时,时,y最大;当时,时,y最大.若 , 时,二次函数的最大值是t,求t的值.(3)、如图,若点P是第一象限抛物线上一点,且 , 求点P的坐标.
(1)、求抛物线解析式;(2)、求开口向下的二次函数的最大值时采用的步骤是:第一,求出二次函数的顶点坐标;第二,确定自变量x的取值范围;第三判定是否在其范围内,若在,则最大值是顶点纵坐标,若不在,要根据其增减性求最大值,即当时,时,y最大;当时,时,y最大.若 , 时,二次函数的最大值是t,求t的值.(3)、如图,若点P是第一象限抛物线上一点,且 , 求点P的坐标.