广西壮族自治区贵港市覃塘区2023年九年级中考一模数学试题

试卷更新日期：2023-04-18 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列四个有理数中，最小的数是（）

A、 $- 1$ B、 $- 2$ C、1 D、0

查看试题解析
2. 如图是一个正方体的表面展开图，若把展开图折叠成正方体，则“识”字一面的对面上的字是（）

A、就 B、是 C、力 D、量

查看试题解析
3. 一种变异的新冠病毒有包膜呈圆形，其直径约125纳米（1纳米 $= 1 0^{- 9}$ 米），将125纳米用科学记数法表示为（）

A、 $1.25 \times 1 0^{- 7}$ 米 B、 $12.5 \times 1 0^{- 8}$ 米 C、 $125 \times 1 0^{- 9}$ 米 D、 $0.125 \times 1 0^{- 6}$ 米

查看试题解析
4. 在平面直角坐标系中，将点 $A (- 2 ， 3)$ 先向右平移4个长度单位，再向下平移5个长度单位得到点B，则点B的坐标是（）

A、 $(4 ， 5)$ B、 $(2 ， 2)$ C、 $(2 ， - 2)$ D、 $(- 2 ， 2)$

查看试题解析
5. 如图，电路图上有3个开关A，B，C和一个小灯泡，同时闭合开关A，C或同时闭合开关B，C都可以使小灯泡发光.下列操作中，使“小灯泡发光”的事件是随机事件的是（）

A、不闭合开关 B、只闭合1个开关 C、只闭合2个开关 D、闭合3个开关

查看试题解析
6.
实数a，b在数轴上对应点的位置如图所示，化简|a|+ $\sqrt{{(a - b)}^{2}}$ 的结果是（　　）

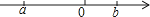A、﹣2a+b B、2a﹣b C、﹣b D、b

查看试题解析
7. 若一个n边形的内角和为900°，则n的值是（）

A、9 B、7 C、6 D、5

查看试题解析
8. 若一元二次方程 $x^{2} - 2 x + m = 0$ 有实数根，则m的取值范围是（）

A、 $m ≥ - 1$ B、 $m \leq - 1$ C、 $m \geq 1$ D、 $m \leq 1$

查看试题解析
9. 如图， $⊙ O$ 是四边形ABCD的外接圆，点E在CD的延长线上，若 $∠ A D E = 80 °$ ，则 $∠ A B C$ 的度数是（）

A、60° B、80° C、90° D、100°

查看试题解析
10. 在一个不透明的袋中装有大小和质地都相同的6个球，每个球上都写有一个汉字，分别为“少”“年”“强”“则”“国”“强”.从中依次任意取出2个球（第1次取出的球不放回袋中），则取出的2个球上为“强”“国”两个汉字的概率是（）

A、 $\frac{1}{15}$ B、 $\frac{1}{10}$ C、 $\frac{1}{9}$ D、 $\frac{2}{15}$

查看试题解析
11. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的顶点坐标为 $(- 1 ， n)$ ，其部分图象如图所示，则以下结论错误的是（）

A、 $a b c > 0$ B、该二次函数的图象经过点 $(- 2 ， - c)$ C、 $3 a + c < 0$ D、关于x的方程 $a x^{2} + b x + c = n + 1$ 无实数根

查看试题解析
12. “赵爽弦图”是我国汉代数学家赵爽为了证明勾股定理而构建的模型图，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形（如图所示），若点E恰好是 $A F$ 的中点， $G E$ 的延长线与 $A B$ 边交于点P，且 $P G = m \cdot P E$ ，则m的值为（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

13. 若 $\sqrt{a + 1}$ 的值为零，则a的值为.

查看试题解析
14. 因式分解： $a^{3} - 4 a =$ ．

查看试题解析
15. 如图，已知 $a ∥ b$ ， $A B ⊥ a$ ， BC与b相交，若 $∠ 1 = 140 °$ ，则 $∠ A B C$ 的度数为.

查看试题解析
16. 16世纪，意大利学者吉罗拉莫·卡尔达诺是第一个系统地推算概率的人，他最初研究的是“掷骰子”游戏中的概率问题.若抛掷一枚均匀的正四面体骰子，骰子每个面上分别刻有1，2，3，4点，则骰子着地一面的点数为偶数的概率为.

查看试题解析
17. 如图，一个圆锥的母线 $B C$ 与底面圆直径 $A B$ 的夹角为 $α$ ，若该圆锥的侧面展开图是圆心角为 $216 °$ 的扇形，则 $c o s α$ 的值为.

查看试题解析
18. 如图，已知正比例函数 $y = \frac{1}{2} x$ 与反比例函数 $y = \frac{k}{x} (k > 0)$ 图象相交于A，B两点，矩形 $A P B Q$ 的两个顶点P，Q均在y轴上，且 $S_{矩形 A P B Q} = 4 \sqrt{5}$ ，则k的值为.

查看试题解析

三、解答题

19. 计算： ${(- 2)}^{3} \times 2^{0} + | \frac{1}{3} - 1 | \div 3^{- 2}$

查看试题解析
20. 先化简，再求值： $(\frac{1}{x + 1} - \frac{1}{x - 1})$ ÷ $\frac{2}{1 - x}$ ，其中 $x = - 2$ .

查看试题解析
21.

(1)、如图，已知 $△ A B C$ ，求作（尺规作图，仅保留痕迹）：
①线段 $A C$ 的垂直平分线 $l_{1}$ ；
② $∠ A B C$ 的平分线 $l_{2}$ .

(2)、在（1）中，设 $l_{1}$ 与 $l_{2}$ 相交于点P，连接 $P A$ ， $P C$ ，若 $P C = A B$ ，则直线 $P A$ 与 $B C$ 的位置关系为.

查看试题解析
22. 在数学实践活动中，将一张平行四边形纸片 $A B C D$ 进行折叠（如图1、2所示），折痕为 $A E$ ，点E在 $B C$ 边上，点B落在点F处.

(1)、如图1，若点F恰好落在 $A D$ 边上，求证：四边形 $A B E F$ 是菱形；

(2)、如图2，若点E是 $B C$ 边的中点，且 $A E = A B = 9$ ， $B C = 12$ ，求 $C F$ 的长.

查看试题解析
23. 某中学开展“弘扬中华传统文化”宣讲活动，为了解宣讲效果，学校政教处从八，九年级分别随机抽取20名学生进行问卷测试（满分：10分，测试成绩均为整数），并将测试结果进行整理分析，请根据以下信息，解答下列问题：
抽取八年级20名学生的测试成绩分别是：5，10，8，9，9，8，9，8，8，6，8，8，10，9，8，8，6，5，10，8；
抽取八，九年级学生测试成绩统计表
年级
平均数
众数
中位数
八年级
8
a
8
九年级
8
b
c

(1)、直接写出表a，b，c的值；

(2)、补全条形统计图；

(3)、你认为该校八，九年级中哪个年级的测试成绩较好？请说明理由（写出一条理由即可）；

(4)、如果该校八，九年级共2000名学生都参加本次问卷测试，请你估计本次问卷测试成绩为满分的八，九年级学生共有多少人？

查看试题解析
24. 某高科技公式根据市场需求，计划生产A、B两种型号的医疗器械，其部分信息如下：
信息一：A、B两种型号的医疗器械共生产80台；
信息二：生产这两种医疗器械的资金超过1800万元，但不足1810万元；
信息三：A，B两种医疗器械的生产成本和售价如下表：
型号
A
B
成本（万元/台）
20
25
售价（万元/台）
24
30
根据上述信息，解答下列问题：

(1)、这两种型号的医疗器械各生产多少台？

(2)、在实际销售时，每台A型医疗器械的售价提高了 $m %$ ，每台B型医疗器械的售价不变，全部销售这两种医疗器械共获得利润595万元，求m的值.（利润 $=$ 售价 $-$ 成本）

查看试题解析
25. 如图，在 $R t △ A B C$ 中， $∠ A B C = 90 °$ ， $B M$ 是边 $A C$ 的中线，将 $△ A B C$ 绕点B顺时针旋转 $90 °$ 得到 $△ D B E$ ， $⊙ O$ 是 $△ D B E$ 的外接圆，点P是 $\overset{⌢}{D E}$ 的中点，连接 $P B$ 交 $D E$ 于点H.

(1)、求证： $B M$ 是 $⊙ O$ 的切线；

(2)、若 $A B = 1$ ， $∠ B A C = 60 °$ ，求 $P H \cdot P B$ 的值.

查看试题解析
26. 如图，在平面直角坐标系 $x O y$ 中，矩形 $O A B C$ 的边 $O A = 3$ ， $A B = 4$ ，点A在x轴的正半轴上，点C在y轴的负半轴上，抛物线 $y = \frac{4}{3} x^{2} + b x + c$ 经过A，C两点，连接 $A C$ .

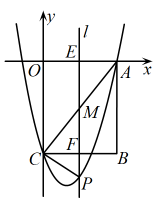(1)、请直接写出b，c的值；

(2)、若动点 $E (m ， 0)$ 在边 $O A$ （不与O，A两点重合）上，过点E作x轴的垂线l交 $B C$ 于点F，交 $A C$ 于点M，交抛物线于点P，连接 $P C$ .
①设线段 $P M$ 的长为h，求h与m的函数关系式；
②当点P在 $B C$ 下方的抛物线上时，以P，C，F为顶点的三角形与 $△ A E M$ 是否相似？若相似，请求出此时点E的坐标；若不相似，请说明理由.

查看试题解析

型号	A	B
成本（万元/台）	20	25
售价（万元/台）	24	30

年级	平均数	众数	中位数
八年级	8	a	8
九年级	8	b	c