广西壮族自治区百色市2023年中考模拟数学试题

试卷更新日期：2023-04-18 类型：中考模拟

进入出卷网下载

一、单选题

1. −2023的绝对值是（）

A、−2023 B、2023 C、±2023 D、 $\frac{1}{2023}$

查看试题解析
2. 一个圆锥如图所示放置，对于它的三视图，下列说法正确的是（）

A、主视图与俯视图相同 B、主视图与左视图相同 C、左视图与俯视图相同 D、三个视图完全相同

查看试题解析
3. 空气是由多种气体混合而成的，为了简明扼要的介绍空气的组成情况，较好的描述数据，最适合使用的统计图是（）

A、扇形图 B、条形图 C、折线图 D、直方图

查看试题解析
4. 下列图形中，是中心对称图形的是（）

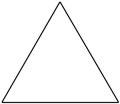A、等边三角形 B、圆 C、正五边形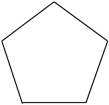 D、扇形

查看试题解析
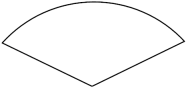5. 希望中学规定学生的学期体育成绩满分为100，其中体育课外活动占20%，期中考试成绩占30%，期末考试成绩占50%.若小强的三项成绩（百分制）依次是95，90，91.则小强这学期的体育成绩是（）

A、92 B、91.5 C、91 D、90

查看试题解析
6. 如图，在Rt△ABC中，∠C=90°，∠B=56°，则∠A的度数为（）

A、 $34 °$ B、 $44 °$ C、 $124 °$ D、 $134 °$

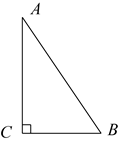查看试题解析
7. 为了驰援上海人民抗击新冠肺炎疫情，柳州多家爱心企业仅用半天时间共筹集到了220000包柳州螺蛳粉，通过专列统一运往上海，用科学记数法将数据220000表示为（）

A、 $0.22 \times 10^{6}$ B、 $2.2 \times 10^{6}$ C、 $22 \times 10^{4}$ D、 $2.2 \times 10^{5}$

查看试题解析
8. 以下调查中，最适合采用抽样调查的是（）

A、了解全国中学生的视力和用眼卫生情况 B、了解全班 $50$ 名同学每天体育锻炼的时间 C、学校招聘教师，对应聘人员进行面试 D、为保证神舟十四号载人飞船成功发射，对其零部件进行检查

查看试题解析
9. 龟兔赛跑之后，输了比赛的兔子决定和乌龟再赛一场．图中的函数图象表示了龟兔再次赛跑的过程（x表示兔子和乌龟从起点出发所走的时间， $y_{1} ， y_{2}$ 分别表示兔子与乌龟所走的路程）．下列说法错误的是（）

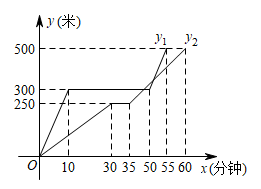A、兔子和乌龟比赛路程是500米 B、中途，兔子比乌龟多休息了35分钟 C、兔子比乌龟多走了50米 D、比赛结果，兔子比乌龟早5分钟到达终点

查看试题解析
10. 如图，在 $△ A B C$ 中，点 $A (3 ， 1)$ ， $B (1 ， 2)$ ，将 $△ A B C$ 向左平移2个单位，再向上平移1个单位，则点B的对应点 $B^{'}$ 的坐标为（）

A、 $(3 ， 1)$ B、 $(3 ， 3)$ C、 $(- 1 ， 1)$ D、 $(- 1 ， 3)$

查看试题解析
11. 如图，在 $△ A B C$ 中， $C A = C B = 4 ， ∠ B A C = α$ ，将 $△ A B C$ 绕点A逆时针旋转 $2 α$ ，得到 $△ A B^{'} C^{'}$ ，连接 $B^{'} C$ 并延长交AB于点D，当 $B^{'} D ⊥ A B$ 时， $\overset{⌢}{B B^{'}}$ 的长是（）

A、 $\frac{2 \sqrt{3}}{3} π$ B、 $\frac{4 \sqrt{3}}{3} π$ C、 $\frac{8 \sqrt{3}}{9} π$ D、 $\frac{10 \sqrt{3}}{9} π$

查看试题解析
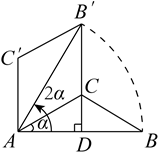12. 如图，在边长为1的菱形 $A B C D$ 中， $∠ A B C = 60 °$ ，动点E在 $A B$ 边上（与点A、B均不重合），点F在对角线 $A C$ 上， $C E$ 与 $B F$ 相交于点G，连接 $A G ， D F$ ，若 $A F = B E$ ，则下列结论错误的是（）

A、 $D F = C E$ B、 $∠ B G C = 120 °$ C、 $A F^{2} = E G \cdot E C$ D、 $A G$ 的最小值为 $\frac{2 \sqrt{2}}{3}$

查看试题解析

二、填空题

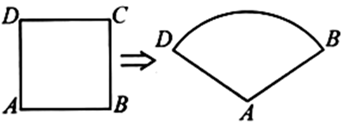
13. 若 $\sqrt{x - 3}$ 在实数范围内有意义，则实数 $x$ 的取值范围是.

查看试题解析
14. 为了进一步落实“作业、睡眠、手机、读物、体质”五项管理要求，某校对学生的睡眠状况进行了调查，经统计得到 $6$ 个班学生每天的平均睡眠时间（单位：小时）分别为： $8$ ， $8$ ， $8$ ， $8.5$ ， $7.5$ ， $9.$ 则这组数据的众数为．

查看试题解析
15. 一元二次方程 $(x - 2) (x + 7) = 0$ 的根是.

查看试题解析
16. 数学课上，老师将如图边长为1的正方形铁丝框变形成以A为圆心， $A B$ 为半径的扇形（铁丝的粗细忽略不计），则所得扇形 $D A B$ 的面积是．

查看试题解析
17. 小韦同学周末的红色之旅，坐爸爸的车去百色起义纪念馆，从家里行驶7千米后，进入高速公路，在高速公路上保持匀速行驶，小韦记录高速公路上行驶的时间（和路程）数据如下表，按照这个速度行驶了2小时进入高速路出口匝道，再行驶5千米抵达纪念馆，则小韦家到纪念馆的路程是千米.

t小时

0.2

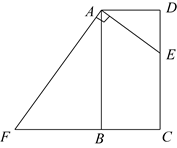
0.6

0.8

s千米

20

60

80

查看试题解析
18. 如图，在正方形ABCD中， $A B = 4 \sqrt{2}$ ，对角线 $A C ， B D$ 相交于点O.点E是对角线AC上一点，连接BE，过点E作 $E F ⊥ B E$ ，分别交 $C D ， B D$ 于点F、G，连接BF，交AC于点H，将 $△ E F H$ 沿EF翻折，点H的对应点 $H^{'}$ 恰好落在BD上，得到 $△ E F H^{'}$ 若点F为CD的中点，则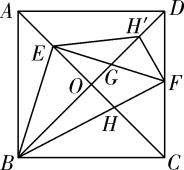 $△ E G H^{'}$ 的周长是.

查看试题解析

三、解答题

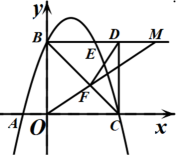
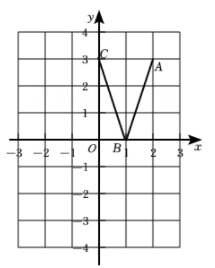
19. 按要求计算下列各题

(1)、计算： $| 1 - \sqrt{3} | + {(2023 - π)}^{0} + {(- \frac{1}{2})}^{- 2} - t a n 6 0^{°}$ ；

(2)、解不等式组： ${\begin{array}{l} 3 x - 5 < 0 ① \\ 1 - \frac{2 x - 4}{3} \leq \frac{5 - x}{2} ② \end{array}$

查看试题解析
20. 如图，在平面直角坐标系中，形如英文字母“V”的图形三个端点的坐标分别是A(2，3)，B(1，0)，C(0，3).

(1)、画出“V”字图形向左平移2个单位后的图形；

(2)、画出原“V”字图形关于x轴对称的图形；

(3)、所得图形与原图形结合起来，你能从中看出什么英文字母？（任意答一个即可）

查看试题解析
21. 如图，小敏在数学实践活动中，利用所学知识对他所在小区居民楼AB的高度进行测量，从小敏家阳台C测得点A的仰角为33°，测得点B的俯角为45°，已知观测点到地面的高度CD＝36m，求居民楼AB的高度（结果保留整数.参考数据：sin33°≈0.55，cos33°≈0.84，tan33°≈0.65）.

查看试题解析
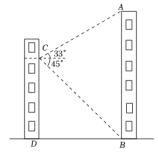22. 为了落实“双减”政策，提倡课内高效学习，课外时间归还学生，“鸿志”班为了激发学生学习热情，提高学习成绩，采用分组学习方案，每7人分为一小组，经过半个学期的学习，在模拟测试中，某小组7人的成绩分别为98，94，92，88，95，98，100（单位：分）.

(1)、该小组学生成绩的中位数是，众数是.

(2)、若成绩95分（含95分）以上评为优秀，求该小组成员成绩的平均分和优秀率（百分率保留整数）.

查看试题解析
23. 在习近平总书记视察广西、亲临柳州视察指导一周年之际，某校开展“紧跟伟大复兴领航人踔厉笃行”主题演讲比赛，演讲的题目有：《同甘共苦民族情》《民族团结一家亲，一起向未来》《画出最美同心圆》。赛前采用抽签的方式确定各班演讲题目，将演讲题目制成编号为 $A$ ， $B$ ， $C$ 的 $3$ 张卡片（如图所示，卡片除编号和内容外，其余完全相同）。现将这 $3$ 张卡片背面朝上，洗匀放好．

(1)、某班从 $3$ 张卡片中随机抽取 $1$ 张，抽到卡片 $C$ 的概率为；

(2)、若七 $(1)$ 班从 $3$ 张卡片中随机抽取 $1$ 张，记下题目后放回洗匀，再由七 $(2)$ 班从中随机抽取 $1$ 张，请用列表或画树状图的方法，求这两个班抽到不同卡片的概率． ( 这 $3$ 张卡片分别用它们的编号 $A$ ， $B$ ， $C$ 表示 )

查看试题解析
24. 梧州市地处亚热带，盛产龙眼.新鲜龙眼的保质期短，若加工成龙眼干（又叫带壳圆肉）则有利于较长时间保存.已知 $3kg$ 的新鲜龙眼在无损耗的情况下可以加工成 $1kg$ 的龙眼干.

(1)、若新鲜龙眼售价为12元/kg，在无损耗的情况下加工成龙眼干，使龙眼干的销售收益不低于新鲜龙眼的销售收益，则龙眼干的售价应不低于多少元/kg?

(2)、在实践中，小苏发现当地在加工龙眼干的过程中新鲜龙眼有6%的损耗，为确保果农的利益，龙眼干的销售收益应不低于新鲜龙眼的销售收益，此时龙眼干的定价取最低整数价格.市场调查还发现，新鲜龙眼以12元/kg最多能卖出 $100kg$ ，超出部分平均售价是5元/kg，可售完.果农们都以这种方式出售新鲜龙眼.设某果农有 $a kg$ 新鲜龙眼，他全部加工成龙眼干销售获得的收益与全部以新鲜龙眼销售获得的收益之差为w元，请写出w与a的函数关系式.

查看试题解析
25. 如图，在矩形 $A B C D$ 中， $A B = 8 ， A D = 4$ ，点E是 $D C$ 边上的任一点（不包括端点D，C），过点A作 $A F ⊥ A E$ 交 $C B$ 的延长线于点F，设 $D E = a$ ．

(1)、求 $B F$ 的长（用含a的代数式表示）；

(2)、连接 $E F$ 交 $A B$ 于点G，连接 $G C$ ，当 $G C // A E$ 时，求证：四边形 $A G C E$ 是菱形．

查看试题解析
26. 已知抛物线经过A（－1，0）、B（0、3）、 C（3，0）三点，O为坐标原点，抛物线交正方形OBDC的边BD于点E，点M为射线BD上一动点，连接OM ，交BC于点F

(1)、求抛物线的表达式；

(2)、求证：∠BOF＝∠BDF ：

(3)、是否存在点M使△MDF为等腰三角形？若不存在，请说明理由；若存在，求ME的长

查看试题解析

t小时	0.2	0.6	0.8
s千米	20	60	80