广西壮族自治区2023年中考一模数学试题

试卷更新日期：2023-04-18 类型：中考模拟

进入出卷网下载

一、单选题

1. $\frac{1}{5}$ 的绝对值是（）

A、 $- 5$ B、5 C、 $- \frac{1}{5}$ D、 $\frac{1}{5}$

查看试题解析
2. 下面几何体的主视图是（）

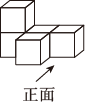A、 B、 C、 D、

查看试题解析
3. 我国神舟十五号载人飞船于 $2022$ 年 $11$ 月 $30$ 日，在距地面约 $390000$ 米的轨道上与中国空间站天和核心舱交会对接成功，将 $390000$ 用科学记数法表示应为（）

A、 $3.9 \times 1 0^{4}$ B、 $39 \times 1 0^{4}$ C、 $39 \times 1 0^{6}$ D、 $3.9 \times 1 0^{5}$

查看试题解析
4. 下列运算正确的（）

A、 ${(x y)}^{2} = x y^{2}$ B、 $x^{3} + x^{3} = 2 x^{3}$ C、 ${(x - y)}^{2} = x^{2} - y^{2}$ D、 $x^{8} \div x^{8} = x$

查看试题解析
5. 不等式 $2 x + 1 \geq 3$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
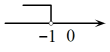6. 九（2）班开展“真爱阅读”活动，该班1月～7月全班同学阅读课外书数量的折线统计图如图所示，下列说法正确的是（）

A、从2月份到6月份阅读课外书的本数逐月下降 B、每月阅读课外书本数的众数是45本 C、每月阅读课外书本数的中位数是58本 D、九（2）班全班4月份的课外书阅读量比5月份的课外书阅读量多

查看试题解析
7. 在平面直角坐标系中，将直线 $y = - 2 x$ 向上平移2个单位，平移后的直线经过点 $(m ， 4)$ ，则m的值为（）

A、 $- 3$ B、 $- \frac{5}{2}$ C、 $- \frac{3}{2}$ D、 $- 1$

查看试题解析
8. 中国清代算书《御制数理精蕴》中有这样一题：“马四匹、牛六头，共价四十八两（我国古代货币单位）；马三匹、牛五头，共价三十八两，问马、牛各价几何？”设马每匹x两，牛每头y两，根据题意可列方程组为（）

A、 ${\begin{array}{l} 6 x + 4 y = 48 ， \\ 5 x + 3 y = 38 \end{array}$ B、 ${\begin{array}{l} 6 x + 4 y = 38 ， \\ 5 x + 3 y = 48 \end{array}$ C、 ${\begin{array}{l} 4 x + 6 y = 48 \\ 3 x + 5 y = 38 \end{array}$ D、 ${\begin{array}{l} 4 x + 6 y = 38 ， \\ 3 x + 5 y = 48 \end{array}$

查看试题解析
9. 某旅游景点2023年1月份共接待游客25万人次，2023年3月份共接待游客65万人次，设每月游客人数的平均增长率为x，则可列方程（）

A、 $25 {(1 + x)}^{2} = 65$ B、 $25 {(1 - x)}^{2} = 65$ C、 $65 {(1 + x)}^{2} = 25$ D、 $65 {(1 - x)}^{2} = 25$

查看试题解析
10. 如图，一辆自行车竖直摆放在水平地面上，右边是它的部分示意图，现测得 $∠ A = 88 °$ ， $∠ C = 42 °$ ， $A B = 60$ ，则点A到 $B C$ 的距离为（）

A、 $60 s i n 50 °$ B、 $\frac{60}{s i n 50 °}$ C、 $60 c o s 50 °$ D、 $60 t a n 50 °$

查看试题解析
11. 如图， $⊙ O$ 的弦 $A C = B D$ ，且 $A C ⊥ B D$ 于点E，连接 $A D$ .若 $A D = 3 \sqrt{6}$ ，则 $⊙ O$ 的半径为（）

A、 $\sqrt{3}$ B、 $2 \sqrt{3}$ C、 $3 \sqrt{3}$ D、3

查看试题解析
12. 定义：如果两个函数图象上至少存在一对点是关于原点对称的，我们则称这两个函数互为“守望函数”，这对点称为“守望点”.例如：点 $P (2 ， 4)$ 在函数 $y = x^{2}$ 上，点 $Q (- 2 ， - 4)$ 在函数 $y = - 2 x - 8$ 上，点P与点Q关于原点对称，此时函数 $y = x^{2}$ 和 $y = - 2 x - 8$ 互为“守望函数”，点P与点Q则为一对“守望点”.已知函数 $y = x^{2} + 2 x$ 和 $y = 4 x + n - 2022$ 互为“守望函数”，则n的最大值为（）

A、 $2020$ B、 $2022$ C、 $2023$ D、 $4084$

查看试题解析

二、填空题

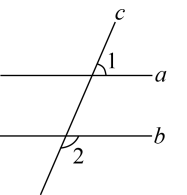
13. 二次根式 $\sqrt{x - 6}$ 有意义的条件是.

查看试题解析
14. 如图，直线a，b被直线c所截，若 $a ∥ b$ ， $∠ 1 = 55 °$ ，则 $∠ 2 =$ .

查看试题解析
15. 因式分解： $a^{2} - 9 =$ ．

查看试题解析
16. 为了落实“双减”政策，减轻学生作业负担，某学校领导随机调查了九（1）班学生每天在作业上共花费的时间，随机调查了该班10名学生，其统计数据如下表：
时间（小时）
4
3
2
1
0
人数
2
4
2
1
1
则这10名学生每天在作业上花费的平均时间是小时.

查看试题解析
17. 如图，等边 $△ A B C$ 内接于 $⊙ O$ ，若 $⊙ O$ 的半径为 $1$ ，以阴影部分为侧面围成一个圆锥，从剩余部分剪出一个圆作为圆锥底面，则这个圆锥的底面积为.

查看试题解析
18. 如图，在平面直角坐标系中，C，A分别为x轴、y轴正半轴上的点，以 $O A ， O C$ 为边，在第一象限内作矩形 $O A B C$ ，且 $S_{矩形 O A B C} = 8 \sqrt{2}$ .将矩形 $O A B C$ 翻折，使点B与原点O重合，折痕为 $M N$ ，点C的对应点 $C^{'}$ 落在第四象限，过点M的反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象恰好过 $M N$ 的中点E，则点E的坐标为.

查看试题解析

三、解答题

19. 计算： $| - 2 | + 3^{2} + 6 \times (- \frac{2}{3}) + {(- 1)}^{2023}$ .

查看试题解析
20. 解分式方程： $\frac{x - 3}{x - 2}$ +1= $\frac{3}{2 - x}$

查看试题解析
21. 如图，四边形 $A B C D$ 是正方形，E是 $B C$ 上一点， $D F ⊥ A E$ 于点F.

(1)、过点B作 $A E$ 的垂线交 $A E$ 于点P（尺规作图，保留痕迹，不写作法）；

(2)、在（1）所作图形中，若 $D F = 4$ ， $P F = 1$ ，求 $C D$ 的长.

查看试题解析
22. 某校随机抽取部分学生，对学生的学习习惯进行问卷调查.设计的问题为：“你在学习新课之前是否有预习的习惯？”答案选项为：A.很少；B.有时；C.常常；D.总是.将调查结果的数据进行了整理，绘制成部分统计图：
请根据图中信息，解答下列问题：

(1)、填空： $a =$ $%$ ， $b =$ $%$ ；“常常”对应扇形的圆心角度数为.

(2)、请你补全条形统计图.

(3)、为了共同进步，李老师从被调查的A类和D类学生中各选出两人，再从两组中分别选取一位学生进行“一帮一”互助学习，请用列表或画树形图的方法求出所选两位同学恰好组合成功（即选择“很少”和“总是”的两人为一组）的概率.

查看试题解析
23. 某商店出售一款商品，经市场调查反映，该商品的日销售量y（件）与销售单价x（元）之间满足一次函数关系，关于该商品的销售单价、日销售量、日销售利润的部分对应数据如下表所示.【注：日销售利润 $=$ 日销售量 $\times$ （销售单价 $-$ 成本单价）】
销售单价x（元）
$75$
$78$
$82$
日销售量y（件）
$150$
$120$
$80$
日销售利润w（元）
$5250$
$4560$
$a$

(1)、填空：该商品的成本单价是元，表中a的值是.

(2)、求该商品日销售利润的最大值.

(3)、由于某种原因，该商品进价降低了m元/件（ $m > 0$ ）.该商店在今后的销售中，规定该商品的销售单价不低于 $68$ 元，日销售量与销售单价仍然满足上表中的函数关系.若日销售利润最大是 $6820$ 元，求m的值.

查看试题解析
24. 如图1，AB是 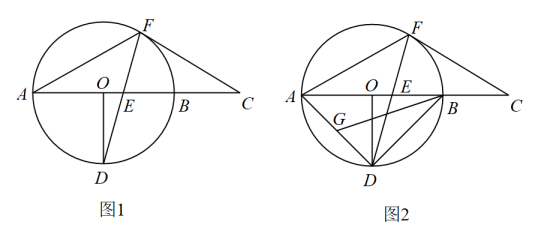$⊙ O$ 的直径，点D，F在 $⊙ O$ 上， $O D ⊥ A B$ ，延长 $A B$ 至点C，连接 $D F$ ，交 $A B$ 于点E，连接 $C F$ ， $C F = C E$ .

(1)、证明： $C F$ 是⊙O的切线；

(2)、如图2，连接 $A D$ ， G是 $A D$ 的中点，连接 $B G$ ，若 $C F = 5$ ， $B C = 3$ ，求 $t a n ∠ A B G$ 的值.

查看试题解析
25. 综合与实践：在学习《解直角三角形》一章时，小邕同学对一个角的倍角的三角函数值与这个角的三角函数值是否有关系产生了浓厚的兴趣，并进行研究.

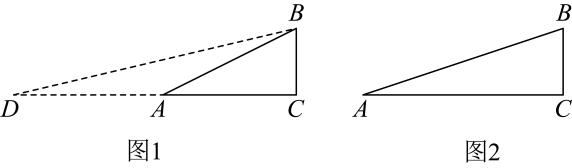(1)、【初步尝试】我们知道： $t a n 60 ° =$ ， $t a n 30 ° =$ .

发现： $t a n A$ $2 t a n (\frac{1}{2} A)$ （填“ $=$ ”或“ $\neq$ ”）.

(2)、【实践探究】在解决“如图1，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 2$ ， $B C = 1$ ，求 $t a n (\frac{1}{2} A)$ 的值”这一问题时，小邕想构造包含 $\frac{1}{2} A$ 的直角三角形，延长 $C A$ 到点D，使 $D A = A B$ ，连接BD，所以可得 $∠ D = \frac{1}{2} ∠ B A C$ ，问题即转化为求 $∠ D$ 的正切值，请按小邕的思路求 $t a n (\frac{1}{2} A)$ 的值.

(3)、【拓展延伸】如图2，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 3$ ， $t a n A = \frac{1}{3}$ .请模仿小邕的思路或者用你的新思路，试着求一求 $t a n 2 A$ 的值.

查看试题解析
26. 如图，抛物线 $y = a (x + 2) (x - 6)$ 与x轴相交于A，B两点，与y轴交于点C，且 $O C = 3$ ，设抛物线的顶点为M，对称轴交x轴于点N.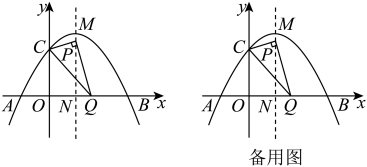

(1)、求抛物线对应的函数表达式和顶点M的坐标；

(2)、P为抛物线的对称轴上一点，且在线段 $M N$ （含端点）上运动， $Q (m ， 0)$ 为x轴上一点，且 $P Q ⊥ P C$ ，求m的最大值；

(3)、在（2）的条件下，当m取最大值时，将线段 $C Q$ 向上平移p个单位长度，使得线段 $C Q$ 与抛物线有两个交点，直接写出p的取值范围.

查看试题解析

销售单价x（元）	$75$	$78$	$82$
日销售量y（件）	$150$	$120$	$80$
日销售利润w（元）	$5250$	$4560$	$a$

时间（小时）	4	3	2	1	0
人数	2	4	2	1	1