广西桂林市2023年九年级中考数学一模试卷
试卷更新日期:2023-04-18 类型:中考模拟
一、单选题
-
1. 反比例函数的比例系数是( )A、1 B、3 C、 D、2. 如图,在中, , , , 则等于( )
 A、 B、 C、 D、3. 下列各统计量中,表示一组数据波动程度的量是( )A、平均数 B、众数 C、方差 D、频率4. 一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根5. 两个相似三角形的周长比是.则其相似比是( )A、 B、 C、 D、6. 如图,直线 , 直线 , 被直线 , , 所截,截得的线段分别为 , , , , 若 , , , 则的长是( )
A、 B、 C、 D、3. 下列各统计量中,表示一组数据波动程度的量是( )A、平均数 B、众数 C、方差 D、频率4. 一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根5. 两个相似三角形的周长比是.则其相似比是( )A、 B、 C、 D、6. 如图,直线 , 直线 , 被直线 , , 所截,截得的线段分别为 , , , , 若 , , , 则的长是( ) A、2 B、 C、 D、67. 用配方法解一元二次方程 x2-10x+11=0,此方程可化为( )A、(x-5)2=14 B、(x+5)2=14 C、(x-5)2 =36 D、(x+5)2 =368. 如图,有一斜坡 , 坡顶B离地面的高度为30m,若坡度 , 则此斜坡的水平距离为( )
A、2 B、 C、 D、67. 用配方法解一元二次方程 x2-10x+11=0,此方程可化为( )A、(x-5)2=14 B、(x+5)2=14 C、(x-5)2 =36 D、(x+5)2 =368. 如图,有一斜坡 , 坡顶B离地面的高度为30m,若坡度 , 则此斜坡的水平距离为( ) A、75m B、50m C、45m D、30m9. 在反比例函数图象的每一支上,y都随x的增大而增大.则k的取值范围是( )A、 B、 C、 D、10. 已知m是一元二次方程的一个根,则的值为( )A、 B、 C、6 D、11. 某中学计划组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),根据报名情况,共安排了15场比赛,则报名参加比赛的球队共有( )A、3支 B、4支 C、5支 D、6支12. 如图,在中, , 以点B为圆心,以合适长度为半径作弧,分别交于N,M两点,再分别以点M,N为圆心,大于MN的长为半径作弧,两弧交于点P,作射线BP交AC于点D,则CD的长度为( )
A、75m B、50m C、45m D、30m9. 在反比例函数图象的每一支上,y都随x的增大而增大.则k的取值范围是( )A、 B、 C、 D、10. 已知m是一元二次方程的一个根,则的值为( )A、 B、 C、6 D、11. 某中学计划组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),根据报名情况,共安排了15场比赛,则报名参加比赛的球队共有( )A、3支 B、4支 C、5支 D、6支12. 如图,在中, , 以点B为圆心,以合适长度为半径作弧,分别交于N,M两点,再分别以点M,N为圆心,大于MN的长为半径作弧,两弧交于点P,作射线BP交AC于点D,则CD的长度为( ) A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
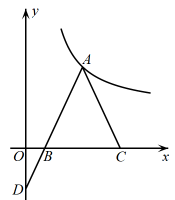
13. 若 , 则.14. 一元二次方程的一般形式是 .15. 一元二次方程 的根是 .16. 某校九(1)班有名学生,期中考试的数学平均成绩是分,九(2)班有名学生,期中考试的数学平均成绩是分,则这两个班期中考试的数学平均成绩是分.17. 如图,在平面直角坐标系中,等腰三角形的底边在x轴的正半轴上,顶点A在反比例函数的图象上,延长交y轴于点D,若 , 则的面积为.
 18. 如图,在等腰中, , , D为边的中点,过点C作于点E,交于点F,则线段的长为.
18. 如图,在等腰中, , , D为边的中点,过点C作于点E,交于点F,则线段的长为.
三、解答题
-
19. 计算:.20. 解一元二次方程:.21. 如图,点D,C分别在 , 上,交于点F, , , , .
 (1)、求证:;(2)、求的长.22. 如图,在平面直角坐标系内三顶点的坐标分别为 , , .
(1)、求证:;(2)、求的长.22. 如图,在平面直角坐标系内三顶点的坐标分别为 , , .
( 1 )画出关于y轴对称的;
( 2 )以点B为位似中心,在点B的下方画出 , 使与位似,且位似比为;
( 3 )直接写出点 , 的坐标.
23. 2022年3月25日,教育部印发《义务教育课程方案和课程标准(2022年版)》,优化了课程设置,将劳动从综合实践活动课程中独立出来,某校计划对初中学生开设“烹饪、种菜、家用小电器维修、课桌椅维修”四门劳动校本课程,学生可以从四门劳动课程中任意选修一门(只选一门).为了解学生对劳动课程的选择意向,教务处随机调查了部分学生,并将调查情况绘制成如图所示的扇形统计图和条形统计图(均不完整).
请根据统计图中的信息,解答下列问题:
(1)、本次调查的样本容量是多少?(2)、在扇形统计图中,“课桌椅维修”对应的圆心角为多少度?(3)、将条形统计图补充完整;(4)、如果该校初中学生共有2000名,那么选择“烹饪”的学生约有多少人?24. 小王计划经营某种时尚产品的专卖店,已知该产品的进货价为70元/件,售价不能低于80元/件,专卖店每月有800元的固定成本开支,根据市场调研,产品的销售量y(件)随着产品的售价x(元/件)的变化而变化,销售量y与售价x之间的部分对应关系如表:售价x(元/件)
80
82
84
86
…
销售量y(件)
500
490
480
470
…
(1)、求销售量y(件)与售价x(元/件)的函数关系式;(2)、小王预计每月盈利8200元,为尽可能让利于顾客,则该产品的售价每件应定为多少元?25. 综合与实践[问题情境]学习完《解直角三角形的应用》后,同学们对如何建立解直角三角形的模型测量物体的实际高度产生了浓厚的兴趣,数学老师决定开展一次主题为《测量学校旗杆高度》的数学实践活动,并为各小组准备了卷尺、测角仪等工具,要求各小组建立测高模型并测量学校旗杆的高度.
[问题探究]第一小组的同学经过讨论,制定出了如下测量实施方案:
第一步,建立测高模型,画出测量示意图(如图1),明确需要测量的数据和测量方法:用卷尺测量测角仪CD的高度和测角仪底部C与旗杆底部A之间的距离,用测角仪测量旗杆顶端B的仰角;
第二步,进行组员分工,制作测量数据记录表;
第三步,选择不同的位置测量三次,依次记录测量数据;
第四步,整理数据,计算旗杆的高,撰写研究报告.
如表是该组同学研究报告中的数据记录和计算结果:
测量组别
的长(米)
的长(米)
仰角
计算的高(米)
位置1
位置2
位置3
平均值
研究结论:旗杆的高为n米
 (1)、表中n的值为;该小组选择不同的位置测量三次,再以三次测量计算的旗杆高度的平均数作为研究结论,这样做的目的是.(2)、该测量模型中,若 , 仰角为 , 用含的代数式表示旗杆的高度为.(3)、[拓展应用]第二小组同学设计的是另外一种测量方案,他们画出的测量示意图如图2,测量时,固定测角仪的高度为m,先在点C处测得旗杆顶端B的仰角 , 然后朝旗杆方向前进m到达点H处,再次测得旗杆顶端B的仰角 , 请你帮他们求出旗杆的高度(结果保留根号).26. 如图,在矩形中, , 以点O为原点,分别以 , 所在直线为x轴,y轴,建立直角坐标系,反比例函数的图象与边交于点 , 交边于点N,连接.
(1)、表中n的值为;该小组选择不同的位置测量三次,再以三次测量计算的旗杆高度的平均数作为研究结论,这样做的目的是.(2)、该测量模型中,若 , 仰角为 , 用含的代数式表示旗杆的高度为.(3)、[拓展应用]第二小组同学设计的是另外一种测量方案,他们画出的测量示意图如图2,测量时,固定测角仪的高度为m,先在点C处测得旗杆顶端B的仰角 , 然后朝旗杆方向前进m到达点H处,再次测得旗杆顶端B的仰角 , 请你帮他们求出旗杆的高度(结果保留根号).26. 如图,在矩形中, , 以点O为原点,分别以 , 所在直线为x轴,y轴,建立直角坐标系,反比例函数的图象与边交于点 , 交边于点N,连接. (1)、求k的值;(2)、求的值(用含n的代数式表示);(3)、将沿翻折,当点C恰好落在x轴上时,求n的值.
(1)、求k的值;(2)、求的值(用含n的代数式表示);(3)、将沿翻折,当点C恰好落在x轴上时,求n的值.