广西2023年初中学业水平考试模拟数学试题(二)
试卷更新日期:2023-04-18 类型:中考模拟
一、单选题
-
1. 下列实数中是无理数的是( )A、 B、 C、 D、2. 下列几何体中,主视图与俯视图的形状不一样的几何体是( )A、
 B、
B、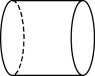 C、
C、 D、
D、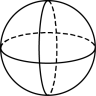 3. 下列运算中,正确的是( )A、 B、 C、 D、4. 据广西壮族自治区统计局消息根据地区生产总值统一核算结果,年全区生产总值亿元,按不变价格计算,比上年增长.数据用科学记数法表示为( )A、 B、 C、 D、5. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
3. 下列运算中,正确的是( )A、 B、 C、 D、4. 据广西壮族自治区统计局消息根据地区生产总值统一核算结果,年全区生产总值亿元,按不变价格计算,比上年增长.数据用科学记数法表示为( )A、 B、 C、 D、5. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 下列事件中,属于必然事件的是( )A、随机购买一张彩票,中奖万 B、抛掷硬币时,反面朝上 C、三角形的两边之和大于第三边 D、经过红绿灯路口,遇到绿灯7.
6. 下列事件中,属于必然事件的是( )A、随机购买一张彩票,中奖万 B、抛掷硬币时,反面朝上 C、三角形的两边之和大于第三边 D、经过红绿灯路口,遇到绿灯7.如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )
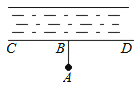 A、两点之间线段最短 B、点到直线的距离 C、两点确定一条直线 D、垂线段最短8. 式子 在实数范围内有意义,那么( )A、 B、 C、 D、9. 为了解某中学八年级600名学生的身高情况,抽查了其中100名学生的身高进行统计分析.下面叙述正确的是( )A、以上调查属于全面调查 B、每名学生是总体的一个个体 C、100名学生的身高是总体的一个样本 D、600名学生是总体10. 不等式组的解集在数轴上表示正确的是( )A、
A、两点之间线段最短 B、点到直线的距离 C、两点确定一条直线 D、垂线段最短8. 式子 在实数范围内有意义,那么( )A、 B、 C、 D、9. 为了解某中学八年级600名学生的身高情况,抽查了其中100名学生的身高进行统计分析.下面叙述正确的是( )A、以上调查属于全面调查 B、每名学生是总体的一个个体 C、100名学生的身高是总体的一个样本 D、600名学生是总体10. 不等式组的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 11. 我国是最早了解勾股定理的国家之一.下面四幅图中,不能用来证明勾股定理的是( )A、
11. 我国是最早了解勾股定理的国家之一.下面四幅图中,不能用来证明勾股定理的是( )A、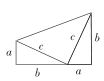 B、
B、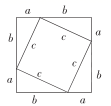 C、
C、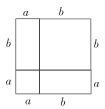 D、
D、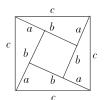 12. 对于任意实数m,n,如果满足 , 那么称这一对数m,n为“完美数对”,记为.若是“完美数对”,则的值为( )A、2 B、3 C、 D、
12. 对于任意实数m,n,如果满足 , 那么称这一对数m,n为“完美数对”,记为.若是“完美数对”,则的值为( )A、2 B、3 C、 D、二、填空题
-
13. 点关于x轴的对称点的坐标为.14. 已知关于的一元二次方程有两个相等的实数根,则 .15. 如图,在等边中,D是边上一点,连接 , 将绕点B逆时针旋转得到 , 连接 , 若 , , 则的周长是.
 16. 圆周率是无限不循环小数.历史上,祖冲之、刘徽、韦达、欧拉等数学家都对有过深入的研究.目前,超级计算机已计算出的小数部分超过万亿位.有学者发现,随着小数部分位数的增加,这个数字出现的频率趋于稳定接近相同,从的小数部分随机取出一个数字,估计数字是的概率为.
16. 圆周率是无限不循环小数.历史上,祖冲之、刘徽、韦达、欧拉等数学家都对有过深入的研究.目前,超级计算机已计算出的小数部分超过万亿位.有学者发现,随着小数部分位数的增加,这个数字出现的频率趋于稳定接近相同,从的小数部分随机取出一个数字,估计数字是的概率为. 17. 如图,已知双曲线经过矩形边的中点F,交于点E,且四边形的面积为3,则k=.
17. 如图,已知双曲线经过矩形边的中点F,交于点E,且四边形的面积为3,则k=.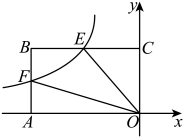 18. 如图所示,在中, , M为线段上一定点,P为线段上一动点.当点P在运动的过程中,满足的值最小时,则.
18. 如图所示,在中, , M为线段上一定点,P为线段上一动点.当点P在运动的过程中,满足的值最小时,则.
三、解答题
-
19. 计算:.20. 解方程: = .21. 如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).

( 1 )请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
( 2 )以点O为位似中心,将△ABC缩小为原来的 ,得到△A2B2C2 , 请在图中y轴右侧,画出△A2B2C2 , 并求出∠A2C2B2的正弦值.
22. 某中学举办“垃圾分类知识答题竞赛”,七年级和八年级根据初赛成绩各选出5名选手参加学校决赛,成绩如图所示.
平均分
中位数
众数
方差
七年级
a
85
b
s2
八年级
85
c
100
160
(1)、直接写出a、b、c的值;(2)、结合两个年级成绩的平均数和中位数进行分析,哪个年级的决赛成绩好;(3)、计算七年级决赛成绩的方差s2 , 并判断哪个年级的选手成绩较为稳定.23. 在中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作交BE的延长线于点F. (1)、求证:;(2)、证明:四边形ADCF是菱形:(3)、若AC=3,AB=4,求菱形ADCF的面积.24. 为了提高同学们学习数学的兴趣,某中学开展主题为“感受数学魅力,享受数学乐趣”的数学活动.并计划购买A、B两种奖品奖励在数学活动中表现突出的学生,已知购买1件A种奖品和2件B种奖品共需元,购买2件A种奖品和1件B种奖品共需元.(1)、每件A、B奖品的价格各是多少元?(2)、根据需要,该学校准备购买A、B两种奖品共件,设购买a件A种奖品,所需总费用为w元,求w与a的函数关系式,并直接写出a的取值范围;(3)、在(2)的条件下,若要求购买的A种奖品的数量不超过B种奖品数量的3倍,求所需总费用的最小值.25. 筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理:如图 , 其原理是利用流动的河水,推动水车转动,水斗舀满河水,将水提升,等水斗转至顶空后再倾入接水槽,水流源源不断,流入田地,以利灌溉.如图 , 筒车与水面分别交于点A,B,筒车上均匀分布着若干盛水筒,P表示筒车的一个盛水筒.接水槽所在的直线是的切线,且与直线交于点M,当点P恰好在所在的直线上时.解决下面的问题:
(1)、求证:;(2)、证明:四边形ADCF是菱形:(3)、若AC=3,AB=4,求菱形ADCF的面积.24. 为了提高同学们学习数学的兴趣,某中学开展主题为“感受数学魅力,享受数学乐趣”的数学活动.并计划购买A、B两种奖品奖励在数学活动中表现突出的学生,已知购买1件A种奖品和2件B种奖品共需元,购买2件A种奖品和1件B种奖品共需元.(1)、每件A、B奖品的价格各是多少元?(2)、根据需要,该学校准备购买A、B两种奖品共件,设购买a件A种奖品,所需总费用为w元,求w与a的函数关系式,并直接写出a的取值范围;(3)、在(2)的条件下,若要求购买的A种奖品的数量不超过B种奖品数量的3倍,求所需总费用的最小值.25. 筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理:如图 , 其原理是利用流动的河水,推动水车转动,水斗舀满河水,将水提升,等水斗转至顶空后再倾入接水槽,水流源源不断,流入田地,以利灌溉.如图 , 筒车与水面分别交于点A,B,筒车上均匀分布着若干盛水筒,P表示筒车的一个盛水筒.接水槽所在的直线是的切线,且与直线交于点M,当点P恰好在所在的直线上时.解决下面的问题: (1)、求证:;(2)、若 , , , 求的长.26. 已知二次函数的图象与x轴交于点A,点B,与y轴交于点C.
(1)、求证:;(2)、若 , , , 求的长.26. 已知二次函数的图象与x轴交于点A,点B,与y轴交于点C. (1)、直接写出点A和点B的坐标.(2)、如图1,若点P是二次函数图象上位于下方的一个动点,连接交于点Q.设点P的横坐标为t,设 , 求w的最大值.(3)、如图2,已知点 , P是二次函数图象上不同于点D的一个动点,连接、、 , 当的面积等于时,求点P的坐标.
(1)、直接写出点A和点B的坐标.(2)、如图1,若点P是二次函数图象上位于下方的一个动点,连接交于点Q.设点P的横坐标为t,设 , 求w的最大值.(3)、如图2,已知点 , P是二次函数图象上不同于点D的一个动点,连接、、 , 当的面积等于时,求点P的坐标.