陕西省西安市新城区2023年中考数学模拟试卷
试卷更新日期:2023-04-18 类型:中考模拟
一、单选题
-
1. 如图,锯木板前,在木板两端固定两个点,用墨盒弹一根墨线然后再锯,这样做的数学道理是( )
 A、两点之间线段最短 B、两点确定一条直线 C、过一点有且只有一条直线与已知直线垂直 D、过直线外一点有且只有一条直线与已知直线平行2. 下列各式中,正确的是( )A、 B、 C、 D、3. 下列说法:
A、两点之间线段最短 B、两点确定一条直线 C、过一点有且只有一条直线与已知直线垂直 D、过直线外一点有且只有一条直线与已知直线平行2. 下列各式中,正确的是( )A、 B、 C、 D、3. 下列说法:①若m满足|m|+m=0,则m<0;②若|a-b|=b-a,则b>a;③若|a|>|b|,则(a+b)(a-b)是正数;④若三个有理数a,b,c,满足 + + =1,则 =1,其中正确的有( )个
A、1 B、2 C、3 D、44. 如图,在平行四边形ABCD中,E为CD延长线上一点,连接BE交AD于F,连接AE,则图中与△DEF相似(不包括本身)的三角形共有( ) A、1个 B、2个 C、3个 D、4个5. 已知,点、在直线上,则与的大小关系是( )A、 B、 C、 D、无法确定6. 某地中午的气温比早晨上升了 , 下午又下降了 , 这两次气温变化的结果是( )A、下降了 B、上升了 C、下降了 D、上升了7. 如图Rt△ABC中,∠BAC=90°,分别以边AB,CA,BC向外作正方形,正方形ABIH的面积为25,正方形BDEC的面积为169,则正方形ACFG的面积是( )
A、1个 B、2个 C、3个 D、4个5. 已知,点、在直线上,则与的大小关系是( )A、 B、 C、 D、无法确定6. 某地中午的气温比早晨上升了 , 下午又下降了 , 这两次气温变化的结果是( )A、下降了 B、上升了 C、下降了 D、上升了7. 如图Rt△ABC中,∠BAC=90°,分别以边AB,CA,BC向外作正方形,正方形ABIH的面积为25,正方形BDEC的面积为169,则正方形ACFG的面积是( ) A、194 B、144 C、122 D、1108. 关于二次函数:的图象有下列命题,其中错误的是( )A、当时,函数的图象经过原点 B、当时,函数的图象关于y轴对称 C、若函数的图象过点 , , 则它的对称轴为直线 D、当且函数的图象开口向下时,方程必有两个不相等的实根
A、194 B、144 C、122 D、1108. 关于二次函数:的图象有下列命题,其中错误的是( )A、当时,函数的图象经过原点 B、当时,函数的图象关于y轴对称 C、若函数的图象过点 , , 则它的对称轴为直线 D、当且函数的图象开口向下时,方程必有两个不相等的实根二、填空题
-
9. 计算的结果是.10. 若的算术平方根是2,则的值为.11. 点A是反比例函数图象上的一点,点B在x轴上,点C是坐标平面上的一点,O为坐标原点,若以点A,B,C,O为顶点的四边形是有一个角为60°的菱形,则点C的坐标是12. 已知M是线段上的黄金分割点若 , 若 , 则.13. 如图,点D为矩形的边的中点,反比例函数的图象经过点D,交边于点E,若的面积为 , 则k=.

三、解答题
-
14. 如图所示, , 相交于点O, , , 与平行吗?为什么?
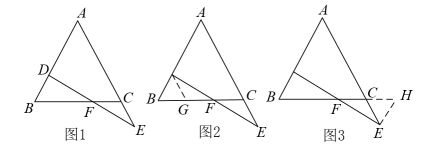
 15. 课堂上,某老师给出一道数学题:如图所示,D点在上,E点在的延长线上,且 , 连接交于F,若F点是的中点,证明:.
15. 课堂上,某老师给出一道数学题:如图所示,D点在上,E点在的延长线上,且 , 连接交于F,若F点是的中点,证明:.小明的思路是:过D作 , 交于点G,如图2;
小丽的思路是:过E作 , 交的延长线于点H,如图3.
请根据小明或小丽的思路任选一种完成该题的证明过程.
 16. 解不等式组17. 解方程或化简分式:(1)、(2)、(3)、18. 为迎接中国共产党成立100周年,让更多人了解红色文化艺术,凝聚和弘扬红色文化,某市举办一百周年红色文旅美术展活动,小唯与小亮都想去观展,但只有一张门票,于是两人想通过摸卡片的方式来决定谁去观展,规则如下:现有两组卡片,第一组卡片上写有A,B,C,第二组卡片上写有A,B,B,C,这两组卡片上除字母外其余均相同.将卡片正面朝下洗匀,随机抽取一张,记下字母后放回,称为摸卡片一次.(1)、若小亮从第二组中摸卡片12次,其中8次摸出的卡片上写有字母B,求这12次摸出的卡片上写有字母B的频率;(2)、小唯从第一组中摸卡片一次,小亮从第二组中摸卡片一次,若摸出的卡片上所写字母均为字母B,则小唯去观展,请用列表或画树状图的方法,求小唯去观展的概率.19. 如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=0.9m,窗高CD=1.1m,并测得OE=0.9m,OF=3m,求围墙AB的高度.
16. 解不等式组17. 解方程或化简分式:(1)、(2)、(3)、18. 为迎接中国共产党成立100周年,让更多人了解红色文化艺术,凝聚和弘扬红色文化,某市举办一百周年红色文旅美术展活动,小唯与小亮都想去观展,但只有一张门票,于是两人想通过摸卡片的方式来决定谁去观展,规则如下:现有两组卡片,第一组卡片上写有A,B,C,第二组卡片上写有A,B,B,C,这两组卡片上除字母外其余均相同.将卡片正面朝下洗匀,随机抽取一张,记下字母后放回,称为摸卡片一次.(1)、若小亮从第二组中摸卡片12次,其中8次摸出的卡片上写有字母B,求这12次摸出的卡片上写有字母B的频率;(2)、小唯从第一组中摸卡片一次,小亮从第二组中摸卡片一次,若摸出的卡片上所写字母均为字母B,则小唯去观展,请用列表或画树状图的方法,求小唯去观展的概率.19. 如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=0.9m,窗高CD=1.1m,并测得OE=0.9m,OF=3m,求围墙AB的高度. 20. 计算:(1)、 ;(2)、 .21. 计算:(1)、(x2y3)4+(-x)8(y6)2;(2)、(9x2y3-27x3y2)÷(3xy)2.22. 在直角坐标系内的位置如图.
20. 计算:(1)、 ;(2)、 .21. 计算:(1)、(x2y3)4+(-x)8(y6)2;(2)、(9x2y3-27x3y2)÷(3xy)2.22. 在直角坐标系内的位置如图.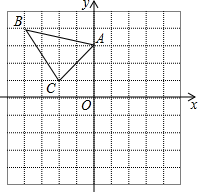 (1)、分别写出A、B、C的坐标;(2)、请在这个坐标系内画出 , 使与关于y轴对称,并写出的坐标;(3)、依次连接点B、、、C得到四边形 , 则四边形的面积为 .23. 为了解某校学生的睡眠情况,该校数学小组随机调查了部分学生一周的平均每天睡眠时间,设每名学生的平均每天睡眠时间为 时,共分为四组:A. ,B. ,C. ,D. ,将调查结果绘制成如图两幅不完整的统计图:
(1)、分别写出A、B、C的坐标;(2)、请在这个坐标系内画出 , 使与关于y轴对称,并写出的坐标;(3)、依次连接点B、、、C得到四边形 , 则四边形的面积为 .23. 为了解某校学生的睡眠情况,该校数学小组随机调查了部分学生一周的平均每天睡眠时间,设每名学生的平均每天睡眠时间为 时,共分为四组:A. ,B. ,C. ,D. ,将调查结果绘制成如图两幅不完整的统计图:
请回答下列问题:
(1)、本次共调查了名学生;(2)、扇形统计图中C组所对应的圆心角大小是;(3)、该校有1500名学生,根据抽样调查结果,请估计该校有多少名学生平均每天睡眠时间低于8时.24. 如图1,在△ABC中,∠BAC=90°,AB=AC=3,D为BC边的中点,∠MDN=90°,将∠MDN绕点D顺时针旋转,它的两边分别交AB、AC于点E、F.
 (1)、求证:△ADE ≌ △CDF;(2)、求四边形AEDF的面积;(3)、如图2,连接EF,设BE=x,求△DEF的面积S与x之间的函数关系式.25. 一食品店平均每天可卖出个某种甜点,卖出个甜点的利润是元,经调查发现,零售单价每下降元,每天可多卖出个甜点,为了使每天获得的利润更多,该店决定把零售单价下降元.(1)、零售单价下降元后,该店平均每天可卖出个甜点,利润是元;(2)、在不考虑其它因素的条件下,当m定为多少元时,才能使该店每天获得的利润是元,并且卖出的甜点更多;(3)、若使该店每天获取的利润最大,m应定为多少元?并求出此时的最大利润.26. 在平面直角坐标系中,四边形是矩形,点 , 点 , 点 , 连接 , 以点A为中心,顺时针旋转矩形 , 旋转角为 , 得到矩形 , 点的对应点分别为.
(1)、求证:△ADE ≌ △CDF;(2)、求四边形AEDF的面积;(3)、如图2,连接EF,设BE=x,求△DEF的面积S与x之间的函数关系式.25. 一食品店平均每天可卖出个某种甜点,卖出个甜点的利润是元,经调查发现,零售单价每下降元,每天可多卖出个甜点,为了使每天获得的利润更多,该店决定把零售单价下降元.(1)、零售单价下降元后,该店平均每天可卖出个甜点,利润是元;(2)、在不考虑其它因素的条件下,当m定为多少元时,才能使该店每天获得的利润是元,并且卖出的甜点更多;(3)、若使该店每天获取的利润最大,m应定为多少元?并求出此时的最大利润.26. 在平面直角坐标系中,四边形是矩形,点 , 点 , 点 , 连接 , 以点A为中心,顺时针旋转矩形 , 旋转角为 , 得到矩形 , 点的对应点分别为. (1)、如图,当点D落在对角线上时,求点D的坐标;(2)、在(1)的情况下,与交于点H.
(1)、如图,当点D落在对角线上时,求点D的坐标;(2)、在(1)的情况下,与交于点H.
①求证;
②求点H的坐标.(3)、为何值时,.(直接写出结果即可).