湖北省孝感市云梦县、应城市、安陆市、孝昌县2023年九年级下学期3月联考数学试题(一模)
试卷更新日期:2023-04-18 类型:中考模拟
一、单选题
-
1. 若收入5元记为 , 则支出4元记为( )A、1 B、 C、4 D、2. 体现我国先进核电技术的“华龙一号”,年发电能力相当于减少二氧化碳排放16320000吨,数16320000用科学记数法表示为( )A、 B、 C、 D、3. 下列立体图形中,俯视图是三角形的是( )A、
 B、
B、 C、
C、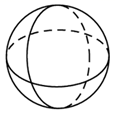 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 下列调查中,最适合采用全面调查的是( )A、了解全国中学生的睡眠时间 B、了解某河流的水质情况 C、调查全班同学的视力情况 D、了解一批灯泡的使用寿命6. 如图,在中,按以下步骤作图:
4. 下列运算正确的是( )A、 B、 C、 D、5. 下列调查中,最适合采用全面调查的是( )A、了解全国中学生的睡眠时间 B、了解某河流的水质情况 C、调查全班同学的视力情况 D、了解一批灯泡的使用寿命6. 如图,在中,按以下步骤作图:①分别过点A、B为圆心,大于的长为半径画弧,两弧交于P、Q两点;②作直线PQ交AB于点D;③以点D为圆心,AD长为半径画弧交PQ于点M、连接AM、BM.若 , 则AM的长为( )
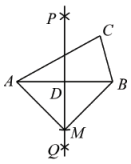 A、4 B、2 C、 D、7. 某校九年级1班学生杨冲家和李锐家到学校的直线距离是和 , 那么杨冲、李锐两家的直线距离不可能是( )A、 B、 C、 D、8. 张老师家、公园、学校依次在同一条直线上,家到公园、公园到学校的距离分别为 , .某天,他从家出发匀速步行到公园后,停留 , 然后匀速步行到学校.设张老师离公园的距离为(单位:),所用时间为(单位:),则下列表示与之间函数关系的图象中,正确的是( )A、
A、4 B、2 C、 D、7. 某校九年级1班学生杨冲家和李锐家到学校的直线距离是和 , 那么杨冲、李锐两家的直线距离不可能是( )A、 B、 C、 D、8. 张老师家、公园、学校依次在同一条直线上,家到公园、公园到学校的距离分别为 , .某天,他从家出发匀速步行到公园后,停留 , 然后匀速步行到学校.设张老师离公园的距离为(单位:),所用时间为(单位:),则下列表示与之间函数关系的图象中,正确的是( )A、 B、
B、 C、
C、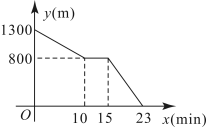 D、
D、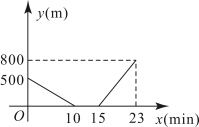
二、填空题
-
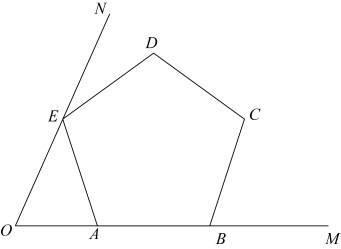
9. 分式在实数范围内有意义,则x的取值范围是.10. 如图所示,已知 , 正五边形的顶点、在射线上,顶点在射线上,则度.
 11. 设 , 是方程的两个实数根,则的值为.12. 有5张仅有编号不同的卡片,编号分别是1,2,3,4,5,从中随机连续抽取2张卡片,其编号都是偶数的概率是.13. 数学课上,老师将如图边长为2的正方形铁丝框变形成以A为圆心,为半径的扇形(铁丝的粗细忽略不计),则所得扇形的面积是.
11. 设 , 是方程的两个实数根,则的值为.12. 有5张仅有编号不同的卡片,编号分别是1,2,3,4,5,从中随机连续抽取2张卡片,其编号都是偶数的概率是.13. 数学课上,老师将如图边长为2的正方形铁丝框变形成以A为圆心,为半径的扇形(铁丝的粗细忽略不计),则所得扇形的面积是.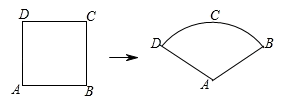 14. 如图,某一时刻太阳光从窗户射入房间内,与地面的夹角 , 已知窗户的高度 , 窗台的高度 , 窗外水平遮阳篷的宽 , 则的长度为.( , , 结果精确到)
14. 如图,某一时刻太阳光从窗户射入房间内,与地面的夹角 , 已知窗户的高度 , 窗台的高度 , 窗外水平遮阳篷的宽 , 则的长度为.( , , 结果精确到) 15. 如图,在平面直角坐标系中,边长为2的正六边形的中心与原点O重合,轴,交y轴于点P.将绕点O顺时针旋转,每次旋转 , 则第次旋转结束时,点A的坐标为.
15. 如图,在平面直角坐标系中,边长为2的正六边形的中心与原点O重合,轴,交y轴于点P.将绕点O顺时针旋转,每次旋转 , 则第次旋转结束时,点A的坐标为. 16. 如图,四边形是正方形,点E为边上一动点,是以点E为直角顶点的等腰直角三角形, , 分别交于点G,H,连接 , .则下列结论:① , ②;③;④当时, , 其中正确结论的序号是.
16. 如图,四边形是正方形,点E为边上一动点,是以点E为直角顶点的等腰直角三角形, , 分别交于点G,H,连接 , .则下列结论:① , ②;③;④当时, , 其中正确结论的序号是.
三、解答题
-
17. 计算:.18. 我国古代数学名著《九章算术》是人类科学史上应用数学的“算经之首”,上面记载有这样一个问题:“今有共买羊,人出五,不足四十五;人出七,不足三.问人数、羊价各几何?”其大意是:今有人合伙买羊,每人出5钱,会差45钱;每人出7钱,会差3钱.问合伙人数、羊价各是多少?请你解答这个问题.19. 为了解某校九年级学生开展“综合与实践”活动的情况,抽样调查了该校名九年级学生上学期参加“综合与实践”活动的天数,并根据调查所得的数据绘制了如下尚不完整的两幅统计图.根据图表信息,解答下列问题:
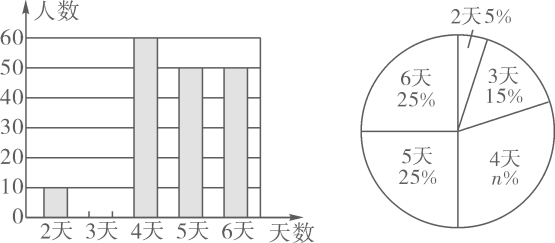 (1)、 , ;(2)、补全条形统计图;(3)、根据抽样调查的结果,请你估计该校九年级2000名学生中上学期参加“综合与实践”活动4天及以上的人数.20. 如图,一次函数与反比例函数()的图像交于点 , , 轴于点 , 轴于点 .
(1)、 , ;(2)、补全条形统计图;(3)、根据抽样调查的结果,请你估计该校九年级2000名学生中上学期参加“综合与实践”活动4天及以上的人数.20. 如图,一次函数与反比例函数()的图像交于点 , , 轴于点 , 轴于点 .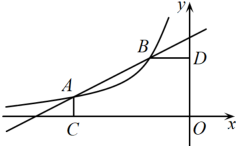 (1)、填空: , , ;(2)、观察图像,直接写出在第二象限内,反比例函数的值大于一次函数的值时的取值范围;(3)、点在线段上,连接 , , 若 , 求点的坐标.21. 如图,是的直径,点C是的中点,过点C的切线与的延长线交于点E,连接 , .
(1)、填空: , , ;(2)、观察图像,直接写出在第二象限内,反比例函数的值大于一次函数的值时的取值范围;(3)、点在线段上,连接 , , 若 , 求点的坐标.21. 如图,是的直径,点C是的中点,过点C的切线与的延长线交于点E,连接 , . (1)、求证:;(2)、若 , , 求的半径.22. 某商场销售的一种商品的进价为元/件,连续销售天后,统计发现:在这天内,该商品每天的销售价格x(元/件)与时间t(第t天)之间满足如图所示的函数关系,该商品的日销售量y(件)与时间t(第t天)之间满足一次函数关系.
(1)、求证:;(2)、若 , , 求的半径.22. 某商场销售的一种商品的进价为元/件,连续销售天后,统计发现:在这天内,该商品每天的销售价格x(元/件)与时间t(第t天)之间满足如图所示的函数关系,该商品的日销售量y(件)与时间t(第t天)之间满足一次函数关系. (1)、直接写出x与t之间的函数关系式;(2)、设销售该商品的日利润为w(元),求w与t之间的函数关系式,并求出在这天内哪天的日利润最大,最大日利润是多少元?(3)、在这天内,日利润不低于元的共有多少天?请直接写出结果.23. 如图1,在中, , 点D,E分别为 , 的中点,连接.将绕点A逆时针旋转(),连接并延长与直线交于点F.
(1)、直接写出x与t之间的函数关系式;(2)、设销售该商品的日利润为w(元),求w与t之间的函数关系式,并求出在这天内哪天的日利润最大,最大日利润是多少元?(3)、在这天内,日利润不低于元的共有多少天?请直接写出结果.23. 如图1,在中, , 点D,E分别为 , 的中点,连接.将绕点A逆时针旋转(),连接并延长与直线交于点F.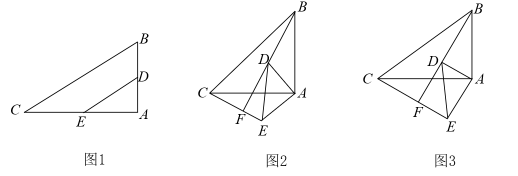 (1)、若 , 将绕点A逆时针旋转至图2所示的位置,则线段与的数量关系是;(2)、若(),将绕点A逆时针旋转,则(1)的结论是否仍然成立?若成立,请就图3所示的情况加以证明;若不成立,请写出正确的结论,并说明理由;(3)、若 , , 将旋转至时,请求出此时的长.24. 如图1,二次函数的图像与x轴交于点 , , 与y轴交于点C.
(1)、若 , 将绕点A逆时针旋转至图2所示的位置,则线段与的数量关系是;(2)、若(),将绕点A逆时针旋转,则(1)的结论是否仍然成立?若成立,请就图3所示的情况加以证明;若不成立,请写出正确的结论,并说明理由;(3)、若 , , 将旋转至时,请求出此时的长.24. 如图1,二次函数的图像与x轴交于点 , , 与y轴交于点C. (1)、求二次函数的解析式;(2)、点P为抛物线上一动点.
(1)、求二次函数的解析式;(2)、点P为抛物线上一动点.①如图2,过点C作x轴的平行线与抛物线交于另一点D,连接 , .当时,求点P的坐标;
②如图3,若点P在直线上方的抛物线上,连接与交于点E,求的最大值.