湖北省武汉市洪山区2023年九年级下学期3月月考数学试卷
试卷更新日期:2023-04-18 类型:中考模拟
一、单选题
-
1. 实数3的相反数是( )A、3 B、 C、 D、2. “成语”是中华文化的瑰宝,是中华文化的微缩景观.下列成语描述的事件是不可能事件的是( )A、水中捞月 B、守株待兔 C、百步穿杨 D、瓮中捉鳖3. 徽章交换是现代奥林匹克运动会特有的文化活动.在2022年北京冬奥会上,徽章交换依然深受欢迎.下列徽章图案中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列运算结果是的是( )A、 B、 C、 D、5. 如图所示,这是由4个大小相同的小正方体摆成的几何体,从左面看到的几何体的形状图是( )
4. 下列运算结果是的是( )A、 B、 C、 D、5. 如图所示,这是由4个大小相同的小正方体摆成的几何体,从左面看到的几何体的形状图是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 如图,电路连接完好,且各元件工作正常,随机闭合开关S1、S2、S3中的两个,能让两个小灯泡同时发光的概率是( )
6. 如图,电路连接完好,且各元件工作正常,随机闭合开关S1、S2、S3中的两个,能让两个小灯泡同时发光的概率是( ) A、 B、 C、 D、7. 点在反比例函数的图象上,下列推断正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、存在 , 使得8. 如图,某容器的底面水平放置,容器上下皆为圆柱形,且大圆柱的底面半径是小圆柱的底面半径的2倍,高度也是小圆柱的2倍,匀速地向此容器内注水,在注满水的过程中,水面的高度h与时间t的函数关系的图象如图所示,则灌满小圆柱时所需时间为( )
A、 B、 C、 D、7. 点在反比例函数的图象上,下列推断正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、存在 , 使得8. 如图,某容器的底面水平放置,容器上下皆为圆柱形,且大圆柱的底面半径是小圆柱的底面半径的2倍,高度也是小圆柱的2倍,匀速地向此容器内注水,在注满水的过程中,水面的高度h与时间t的函数关系的图象如图所示,则灌满小圆柱时所需时间为( ) A、 B、 C、 D、109. 如图,是的内切圆, , 过点I作分别交 , 于N,M,若 , , 则的半径是( )
A、 B、 C、 D、109. 如图,是的内切圆, , 过点I作分别交 , 于N,M,若 , , 则的半径是( )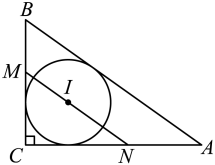 A、 B、 C、 D、10. 方程 的根可视为函数 的图象与函数 的图象交点的横坐标,那么用此方法可推断出方程 的实数根x所在的范围是( )A、 B、 C、 D、
A、 B、 C、 D、10. 方程 的根可视为函数 的图象与函数 的图象交点的横坐标,那么用此方法可推断出方程 的实数根x所在的范围是( )A、 B、 C、 D、二、填空题
-
11. 计算 的结果是12. 为了增强学生预防甲流的安全意识,某校开展甲流防控知识竞赛.来自不同年级的26名参赛同学的得分情况如图所示,这些成绩的中位数是.
 13. 分式方程的解是.14. 如图,有甲乙两座建筑物,从甲建筑物点处测得乙建筑物点的俯角为 , 点的俯角为 , 为两座建筑物的水平距离.已知乙建筑物的高度为 , 则甲建筑物的高度为.( , , , 结果保留整数).
13. 分式方程的解是.14. 如图,有甲乙两座建筑物,从甲建筑物点处测得乙建筑物点的俯角为 , 点的俯角为 , 为两座建筑物的水平距离.已知乙建筑物的高度为 , 则甲建筑物的高度为.( , , , 结果保留整数).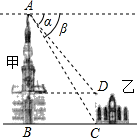 15. 抛物线 ( )的对称轴为 ,经过点(1,n),顶点为P,下列四个结论:
15. 抛物线 ( )的对称轴为 ,经过点(1,n),顶点为P,下列四个结论:①若 ,则 ;
②若c与n异号,则抛物线与x轴有两个不同的交点;
③方程 一定有两个不相等的实数解;
④设抛物线交y轴于点C,不论a为何值,直线PC始终过定点(3,n).
其中正确的是(填写序号).
16. 如图四边形中, , , , E为线段的中点,连接交线段于F,若 , , 则的长为.
三、解答题
-
17. 解不等式组请按下列步骤完成解答.(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来:
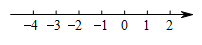 (4)、原不等式组的解集是.18. 如图, , , .
(4)、原不等式组的解集是.18. 如图, , , . (1)、求的度数;(2)、若平分 , 求的度数.19. 近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.
(1)、求的度数;(2)、若平分 , 求的度数.19. 近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)、本次一共调查了多少名购买者?(2)、请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.(3)、若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?20. 如图,AB是⊙O的直径,C是⊙O上一点,∠ACB的平分线交AB于E,交⊙O于D,连接AD,BD. (1)、求证:;(2)、若 , , 求的值.21. 如图,在正方形的网格中,点A,B,C均在格点上,点P为线段与网格线的交点,仅用无刻度的直尺完成以下作图,画图过程用虚线表示.
(1)、求证:;(2)、若 , , 求的值.21. 如图,在正方形的网格中,点A,B,C均在格点上,点P为线段与网格线的交点,仅用无刻度的直尺完成以下作图,画图过程用虚线表示. (1)、在图1中,将线段绕点A逆时针旋转得到线段;连接交于F,则 .(2)、在图2中,在线段上画点Q,连接 , 使得(3)、在图3中,分别在线段 , 线段上画M,N连接 , , 使得最小.22. 冰墩墩是2022年北京冬季奥运会的吉祥物.冰墩墩以熊猫为原型设计,寓意创造非凡、探索未来.某批发市场购进一批冰墩墩玩偶出售,每件进货价为50元.经市场调查,每月的销传量y(万件)与每件的售价x(元)满足一次函数关系,部分数据如下表:
(1)、在图1中,将线段绕点A逆时针旋转得到线段;连接交于F,则 .(2)、在图2中,在线段上画点Q,连接 , 使得(3)、在图3中,分别在线段 , 线段上画M,N连接 , , 使得最小.22. 冰墩墩是2022年北京冬季奥运会的吉祥物.冰墩墩以熊猫为原型设计,寓意创造非凡、探索未来.某批发市场购进一批冰墩墩玩偶出售,每件进货价为50元.经市场调查,每月的销传量y(万件)与每件的售价x(元)满足一次函数关系,部分数据如下表:售价x(元/件)
60
62
68
销售量y(万件)
40
36
24
(1)、直接写出y与x之间的函数表达式为;(2)、批发市场销售冰墩墩玩偶希望每月获利352万元,且尽量给客户实惠,每件冰墩墩应该如何定价?(3)、批发市场规定,冰墩墩的每件利润率不低于10%,若这批玩偶每月销售量不低于20a万件,最大利润为400万元,求a的值.23. (1)、问题发现如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
(1)、问题发现如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:① 的值为;
②∠AMB的度数为.
(2)、类比探究如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断 的值及∠AMB的度数,并说明理由;
(3)、拓展延伸在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB= ,请直接写出当点C与点M重合时AC的长.
24. 如图1,抛物线与x轴交于A,B(点A在点B左侧),与y轴负半轴交于C,且满足OA=OB=OC=2.

 (1)、求抛物线的解析式;(2)、如图2,D为y轴负半轴上一点,过D作直线l垂直于直线BC,直线l交抛物线于E,F两点(点E在点F右侧),若DF=3DE,求D点坐标;(3)、如图3,点M为抛物线第二象限部分上一点,点M,N关于y轴对称,连接MB,P为线段MB上一点(不与M、B重合),过P点、直线x=t(t为常数)交x轴于S,交直线NB于Q,求QS-PS的值(用含t的代数式表示).
(1)、求抛物线的解析式;(2)、如图2,D为y轴负半轴上一点,过D作直线l垂直于直线BC,直线l交抛物线于E,F两点(点E在点F右侧),若DF=3DE,求D点坐标;(3)、如图3,点M为抛物线第二象限部分上一点,点M,N关于y轴对称,连接MB,P为线段MB上一点(不与M、B重合),过P点、直线x=t(t为常数)交x轴于S,交直线NB于Q,求QS-PS的值(用含t的代数式表示).