湖北省十堰市郧西县2023年九年级3月学业水平监测数学试题
试卷更新日期:2023-04-18 类型:中考模拟
一、单选题
-
1. 5的相反数为( )A、 B、-5 C、5 D、-2. 如图, ,点P为 上一点, 平分 ,若 ,则 的大小为( )
 A、50° B、55° C、60° D、65°3. 如图是由5个相同的小正方体搭成的几何体,它的左视图是( )
A、50° B、55° C、60° D、65°3. 如图是由5个相同的小正方体搭成的几何体,它的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( )A、 B、 C、 D、5. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
4. 下列计算正确的是( )A、 B、 C、 D、5. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:甲
乙
丙
丁
平均数(cm)
185
180
185
180
方差
3.6
3.6
7.4
8.1
根据表数据,从中选择一名成绩好且发挥稳定的参加比赛,应该选择( )
A、甲 B、乙 C、丙 D、丁6. 《孙子算经》中有一道题,原文是:今有三人共车,二车空:二人共车,九人步,问人与车各几何?译文为:今有若干人乘车,每3人共乘一车,最终剩余2辆车:若每2人共乘一车,最终剩余9个人无车可乘,问共有多少人,多少辆车?设共有x人,可列方程( )A、 B、 C、 D、7. 如图,在四边形 中,点P是边 上的动点,点Q是边 上的定点,连接 , 分别是 的中点,连接 .点P在由C到D运动过程中,线段EF的长度( ) A、保持不变 B、逐渐变小 C、先变大,再变小 D、逐渐变大8. 如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆低端D到大楼前梯砍底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1: ,则大楼AB的高度约为( )(精确到0.1米,参考数据: )
A、保持不变 B、逐渐变小 C、先变大,再变小 D、逐渐变大8. 如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆低端D到大楼前梯砍底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1: ,则大楼AB的高度约为( )(精确到0.1米,参考数据: )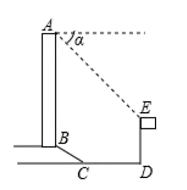 A、30.6米 B、32.1 米 C、37.9米 D、39.4米9. 如图,AB为⊙O的弦,点C在AB上,AC=4,BC=2,CD⊥OC交⊙O于点D,则CD的长为( )
A、30.6米 B、32.1 米 C、37.9米 D、39.4米9. 如图,AB为⊙O的弦,点C在AB上,AC=4,BC=2,CD⊥OC交⊙O于点D,则CD的长为( ) A、 B、3 C、 D、10. 如图,的直角顶点O为坐标原点,点A在反比例函数的图象上,点B在反比例函数的图象上,交y轴于点C,则k的值为( )
A、 B、3 C、 D、10. 如图,的直角顶点O为坐标原点,点A在反比例函数的图象上,点B在反比例函数的图象上,交y轴于点C,则k的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 我国持续开展大规模国土绿化,人工林稳步发展,面积稳居世界第一,目前,我国人工林面积达8100万公顷.将数字81000000用科学记数法表示为.12. 不等式组 的所有整数解的和为.13. 如果三角形的一个外角等于与它相邻的内角的4倍,等于与它不相邻的一个内角的2倍,则此三角形最小内角的度数是.14. 如图,正方形的边长为1,以为边作第二个正方形 , 再以为边作第三个正方形…,按照这样规律作下去,第10个正方形的边长为.
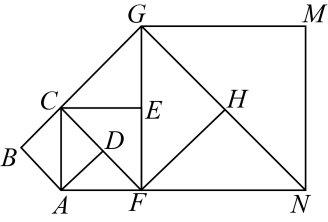 15. 如图,曲线和是两个半圆, , 大半圆半径为4,则阴影部分的面积是 .
15. 如图,曲线和是两个半圆, , 大半圆半径为4,则阴影部分的面积是 . 16. 如图,正方形的边长为1,的平分线交于点E.若点P,Q分别是和上的动点,则的最小值是.
16. 如图,正方形的边长为1,的平分线交于点E.若点P,Q分别是和上的动点,则的最小值是.
三、解答题
-
17. 计算:.18. 化简:.19. 已知关于x的一元二次方程 有两个不相等的实数根.(1)、求实数m的取值范围;(2)、若该方程的两个根都是符号相同的整数,求整数m的值.20. 某校为了响应市政府“创建文明城市”号召,依次开展了“A:文明礼仪,B:环境保护,C:垃圾分类,D:卫生保洁”四个主题的系列实践活动,每个学生选择一个主题参与活动.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下不完整的频数分布表和扇形统计图.
活动类别
频数
A
35
B
C
15
D
 (1)、本次调查的学生人数是人, ;(2)、该校共有学生800人,试估计该校参加“垃圾分类”主题实践活动的学生约有多少人?(3)、在本次系列主题活动中,某班有甲、乙、丙、丁四位同学表现特别优秀,现要从中随机选取两位同学分别参加学校的两项交流活动,求甲同学被选中的概率.21. 在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)、本次调查的学生人数是人, ;(2)、该校共有学生800人,试估计该校参加“垃圾分类”主题实践活动的学生约有多少人?(3)、在本次系列主题活动中,某班有甲、乙、丙、丁四位同学表现特别优秀,现要从中随机选取两位同学分别参加学校的两项交流活动,求甲同学被选中的概率.21. 在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F. (1)、求证:四边形ADCF是菱形;(2)、若AC=4,AB=5,求菱形ADCF的面积.22. 如图,AD是⊙O的直径,BA=BC,BD交AC于点E,点F在DB的延长线上,且∠BAF=∠C.
(1)、求证:四边形ADCF是菱形;(2)、若AC=4,AB=5,求菱形ADCF的面积.22. 如图,AD是⊙O的直径,BA=BC,BD交AC于点E,点F在DB的延长线上,且∠BAF=∠C. (1)、求证:AF是⊙O的切线;(2)、若BC=2 ,BE=4,求⊙O半径r.23. 某商场销售的一种商品的进价为30元/件,连续销售100天后,统计发现:在这100天内,①该商品每天的销售价格x(元/件)与时间(第1天)满足关系式: ;
(1)、求证:AF是⊙O的切线;(2)、若BC=2 ,BE=4,求⊙O半径r.23. 某商场销售的一种商品的进价为30元/件,连续销售100天后,统计发现:在这100天内,①该商品每天的销售价格x(元/件)与时间(第1天)满足关系式: ;②该商品的日销售量y(件)与时间t(第t天)满足一次函数关系,部分数据如下表:
时间t(第t天)
1
2
10
20
……
日销售量y(件)
119
118
110
100
……
(1)、直接写出y与t之间的函数解析式:(2)、设销售该商品的日利润为w(元),请直接写出w与t之间的函数解析式,并求出在这100天内哪天的日利润最大,最大日利润是多少元?(3)、在这100天内,日利润不低于4000元的共有多少天,请直接写出结果.24. 已知∠ABC=90°,BA=BC,在同一平面内将等腰直角△ABC绕顶点A逆时针旋转(旋转角小于180°)得△ADE. (1)、若AE//BD如图(1),求旋转角∠BAD度数;(2)、当旋转角为60°时,延长ED与BC交于点F,如图(2).求证:AC平分∠DAF(3)、点P是边BC上动点,将AP绕点A逆时针旋转15°到AG,如图(3)示例,设AB=BC= , 求CG长度最小值(用含式子表示)25. 如图1,抛物线 与 轴交于点 、点 ,与 轴交于点 ,顶点 的横坐标为1,对称轴交 轴交于点 ,交 与点 .
(1)、若AE//BD如图(1),求旋转角∠BAD度数;(2)、当旋转角为60°时,延长ED与BC交于点F,如图(2).求证:AC平分∠DAF(3)、点P是边BC上动点,将AP绕点A逆时针旋转15°到AG,如图(3)示例,设AB=BC= , 求CG长度最小值(用含式子表示)25. 如图1,抛物线 与 轴交于点 、点 ,与 轴交于点 ,顶点 的横坐标为1,对称轴交 轴交于点 ,交 与点 . (1)、求顶点 的坐标;(2)、如图2所示,过点 的直线交直线 于点 ,交抛物线于点 .
(1)、求顶点 的坐标;(2)、如图2所示,过点 的直线交直线 于点 ,交抛物线于点 .①若直线 将 分成的两部分面积之比为 ,求点 的坐标;
②若 ,求点 的坐标.