广西壮族自治区梧州市岑溪市2021-2022学年八年级下学期期中数学试题

试卷更新日期：2023-04-18 类型：期中考试

进入出卷网下载

一、单选题

1. 要使二次根式 $\sqrt{x + 1}$ 有意义，字母x的取值必须满足（）

A、 $x \geq 0$ B、 $x \leq 0$ C、 $x \geq 1$ D、 $x \geq - 1$

查看试题解析
2. 下列二次根式能与 $\sqrt{3}$ 合并的是（）．

A、 $\sqrt{12}$ B、 $\sqrt{10}$ C、 $\sqrt{8}$ D、 $\sqrt{6}$

查看试题解析
3. 下列方程中，是一元二次方程的是（）

A、 $x - 3 x = 4$ B、 $x^{2} - \frac{2}{x} = 3$ C、 $x^{3} - 3 = 7$ D、 $x^{2} + 2 x - 6 = 0$

查看试题解析
4. 下列运算中，正确的是（）

A、 $\sqrt{{(- 5)}^{2}} = - 5$ B、 $3 \sqrt{2} - \sqrt{2} = 3$ C、 ${(\sqrt{2} + \sqrt{3})}^{2} = 5$ D、 ${(- \sqrt{3})}^{2} = 3$

查看试题解析
5. 方程x²＝4x的解是（）

A、x＝4 B、x＝2 C、x＝4或x＝0 D、x＝0

查看试题解析
6. 用配方法将方程 $x^{2} + 6 x - 11 = 0$ 变形，正确的是（）

A、 ${(x - 3)}^{2} = 20$ B、 ${(x - 3)}^{2} = 2$ C、 ${(x + 3)}^{2} = 2$ D、 ${(x + 3)}^{2} = 20$

查看试题解析
7. 已知一个直角三角形的两边长分别为3和4，则第三边长是（）

A、5 B、25 C、 $\sqrt{7}$ D、5或 $\sqrt{7}$

查看试题解析
8. 已知关于 $x$ 的一元二次方程 $(a - 1) x^{2} - 2 x + 1 = 0$ 有实数根，则 $a$ 的取值范围是（）

A、 $a \leq 2$ B、 $a > 2$ C、 $a \leq 2$ 且 $a \neq 1$ D、 $a < - 2$

查看试题解析
9. 已知三角形两边长分别为2和9，第三边的长为二次方程x²-14x+48=0的一根，则这个三角形的周长为（）

A、11 B、17 C、19 D、17或19

查看试题解析
10. 如图，有两颗树，一颗高10米，另一颗高4米，两树相距8米．一只鸟从一颗树的树梢飞到另一颗树的树梢，问小鸟至少飞行（）

A、8米 B、10米 C、12米 D、14米

查看试题解析
11. 如图，在宽为20米、长为30米的矩形地面上修建两条同样宽的道路，余下部分作为耕地．若耕地面积需要551米² ，则修建的路宽应为（）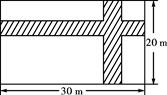

A、1米 B、1.5米 C、2米 D、2.5米

查看试题解析
12. 若实数a在数轴上的位置如图所示，则化简 $\sqrt{(a + 1)^{2}} + \sqrt{(a - 2)^{2}}$ 的结果是（）

A、3 B、-3 C、2a-1 D、1-2a

查看试题解析

二、填空题

13. 比较大小：4 $\sqrt{17}$ （填“>”“<”或“=”）.

查看试题解析
14. 如图，一棵大树在一次强台风中距地面5 $m$ 处折断，倒下后树顶端着地点A距树底端B的距离为12 $m$ ，这棵大树在折断前的高度为.

查看试题解析
15. 一元二次方程2x²-x+1＝0的根的情况是实数根（填“有”或“没有”）.

查看试题解析
16. $\sqrt{3}$ 与最简二次根式 $\sqrt{m + 1}$ 是同类二次根式，则m＝.

查看试题解析
17. 某超市销售一种水果，每月可售出500千克，每千克盈利10元.经市场分析，售价每涨1元，月销售量将减少10千克.如果该超市销售这种水果每月盈利8000元，那么该水果的单价涨了多少元？设水果单价涨了x元，根据题意，可列方程为.

查看试题解析
18. 如图，在一个高为5m ，长为13m的楼梯表面铺地毯，则地毯的长度至少是．

查看试题解析

三、解答题

19. 计算： $\sqrt{27} - \sqrt{2} \times \sqrt{6} + \sqrt{18}$ .

查看试题解析
20. 请任意选择下列其中的一个方程作答，并用适当的方法解这个方程.

(1)、x²+2x-3＝0

(2)、x²-3x+1＝0.

查看试题解析
21. 已知：如图，在Rt△ABC中，∠ACB＝90°，AC＝8cm，BC＝6cm，CD⊥AB于D，求：

(1)、斜边AB的长；

(2)、高CD的长.

查看试题解析
22. 已知关于x的方程 $x^{2} + 2 k x + k^{2} - 1 = 0$ .试说明：无论k取何值时，方程总有两个不相等的实数根.

查看试题解析
23. 先化简，再求值： $\frac{a^{2} + 2 a + 1}{a + 2} \div \frac{a^{2} - 1}{a - 1} - \frac{a}{a + 2}$ ，其中a $= \sqrt{3} -$ 2.

查看试题解析
24. 已知实数x，y满足y $= \sqrt{x - 13} + \sqrt{13 - x} +$ 5，求：

(1)、x与y的值；

(2)、x²-y²的平方根.

查看试题解析
25. 如图，为建设美丽校园，学校准备利用一面围墙和旁边的空地，建一个面积为160m²的长方形花坛，另三边用木质围栏围成，木栏总长36m，若围墙足够长，则花坛垂直于墙的一边长应安排多少米？

查看试题解析
26. 2013年，东营市某楼盘以每平方米6500元的均价对外销售，因为楼盘滞销，房地产开发商为了加快资金周转，决定进行降价促销，经过连续两年下调后，2015年的均价为每平方米5265元．

(1)、求平均每年下调的百分率.

(2)、假设2016年的均价仍然下调相同的百分率，张强准备购买一套100平方米的住房，他持有现金20万元，可以在银行贷款30万元，张强的愿望能否实现？（房价每平方米按照均价计算）

查看试题解析