广西壮族自治区来宾市忻城县2021-2022学年八年级下学期期中数学试题

试卷更新日期：2023-04-18 类型：期中考试

进入出卷网下载

一、单选题

1. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，则与∠A互余的角有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ， CD是斜边AB上的中线，且 $B C = C D$ ，则∠B的度数等于（）

A、30° B、45° C、60° D、90°

查看试题解析
3. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， D是AB中点，DE⊥AC于点E， $∠ A = 30 °$ ， $A B = 12$ ，则DE的长等于（）

A、6 B、5 C、4 D、3

查看试题解析
4. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ，且 $A B = 10$ ， $B C = 6$ ，则AC等于（）

A、12 B、8 C、4 D、2

查看试题解析
5. 如图，一架梯子AB长为5米，顶端A靠在墙AC上，这时梯子下端B与墙底端C的距离是3米，梯子下滑后停在DE的位置上，这时测得BE为1米，则梯子顶端A下滑了（）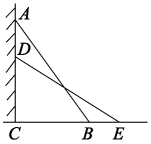

A、1米 B、1.5米 C、2米 D、2.5米

查看试题解析
6. 下列各组线段能构成直角三角形的一组是（）

A、1，2，3 B、6，10，8 C、12，13，25 D、3，4，6

查看试题解析
7. 判断两个直角三角形全等的方法不正确的有（　　）

A、两条直角边对应相等 B、斜边和一锐角对应相等 C、斜边和一条直角边对应相等 D、两个锐角对应相等

查看试题解析
8. 从多边形的一个顶点出发可引出7条对角线，则它是（）

A、七边形 B、八边形 C、九边形 D、十边形

查看试题解析
9. 如图，在 $▱ A B C D$ 中，E，F是对角线AC上的点，如果添加一个条件，使 $△ A D E ≌ △ C B F$ ，则添加的条件不能为（）

A、 $∠ 1 = ∠ 2$ B、 $A F = C E$ C、 $D E = B F$ D、 $A E = C F$

查看试题解析
10. 下列图形：①圆；②菱形；③平行四边形；④矩形中，既是轴对称图形又是中心对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. 如图，在菱形 $A B C D$ 中，对角线 $A C$ ， $B D$ 分别为16和12， $D E ⊥ A B$ 于点E，则 $D E =$ （）

A、 $\frac{48}{5}$ B、 $\frac{96}{5}$ C、10 D、8

查看试题解析
12. 如图，正方形ABCD的面积为16，点E为正方形内一点，且 $△ A B E$ 为等边三角形，点P为正方形对角线AC上的点，则 $P D + P E$ 的最小值为（）

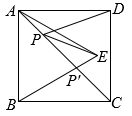A、3 B、4 C、5 D、6

查看试题解析

二、填空题

13. 在Rt△ABC中，已知∠C=90°，∠B=46°，则∠A的度数为．

查看试题解析
14. 已知一个三角形的三边之比为 $1 ： 2 ： \sqrt{3}$ ，则这个三角形的最小角等于度.

查看试题解析
15. 菱形ABCD的一个内角为120°，边长为6，则这个菱形较长的对角线长＝.

查看试题解析
16. 如图，在 $▱ A B C D$ 中，对角线AC与BD交于点O，点E是CD中点， $A D = 20$ ，则OE的长为.

查看试题解析
17. 如图，AD是 $R t △ A B C$ 的角平分线， $A B = 12$ ， $A C = 8$ ，则 $△ A B D$ 的面积与 $△ A C D$ 的面积之比是.

查看试题解析
18. 如图，将矩形 $A B C D$ 沿直线 $A E$ 折叠，顶点 $D$ 恰好落在 $B C$ 边上 $F$ 点处，已知 $C E = 3 c m$ ， $A B = 8 c m$ ，则图中阴影部分面积为

查看试题解析

三、解答题

19. 如图，已知 $∠ A B C = ∠ A D C = 90 °$ ， E是AC上一点，且 $A B = A D$ ，求证： $B E = D E$ .

查看试题解析
20. 如图，公路OA与OB相交于点O，在两条公路相交内部有两个村庄E，F，现要修建一个电站，使得该电站到两条公路OA和OB的距离相等，且到两个村庄的距离相等.请你用尺规作出该电站的位置.（不写作法，保留作图痕迹，写出结论）

查看试题解析
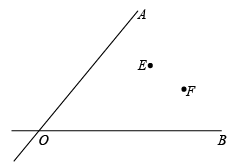21. 如果一个多边形的每一个外角都等于与它相邻的内角，那么这个多边形是几边形？求这个多边形的每一个内角是多少度.

查看试题解析
22. 钓鱼岛自古以来就是中国的神圣领土，为宣誓主权，我海监船编队奉命在钓鱼岛附近进行维权活动，如图，一艘海监船以60海里/小时的速度向正北方向航行，海监船在A处，测得钓鱼岛P在该船的北偏东30°方向上，航行半小时后，该船到达点B处，发现此时该船与钓鱼岛P的距离最短.

(1)、请在图中作出点B的位置；

(2)、求钓鱼岛P到点B的距离.

查看试题解析
23. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， DE垂直平分AB，BD是∠ABC的平分线.

(1)、求∠A的度数：

(2)、若 $A B = 8$ ，求AD的长.

查看试题解析
24. 如图，E，F，G，H分别是矩形ABCD各边的中点，依次顺序连接各边中点得到四边形EFGH.

(1)、猜想四边形EFGH是什么特殊四边形？

(2)、对你的猜想给予证明.

查看试题解析
25. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， AD平分∠BAC，交BC于点D，DE⊥AB于E，点F在AC上，且 $D F = B D$ .

(1)、求证： $B E = C F$ ；

(2)、若 $A B = 20$ ， $A F = 8$ ，求BE的长.

查看试题解析
26. 如图①，在正方形ABCD中，P是CD边上一个动点（P与C，D不重合），以CP为边在正方形ABCD外作矩形PCEF，连接AP，DE，且 $B P = D E$ .

(1)、求证：矩形PCEF是正方形；

(2)、在图①中，连接AP，当点P在什么位置时， $A P = D E$ ？请证明；

(3)、将图①中的正方形PCEF绕点C按顺时针方向旋转任意角度，得到如图②的情形，请你猜想图②中BP与DE的位置关系与数量关系，并证明你的结论.

查看试题解析