广西壮族自治区贵港市桂平市2021-2022学年八年级下学期期中数学试题
试卷更新日期：2023-04-18 类型：期中考试
一、单选题
-
1. 在△ABC中，若∠A＝90°，∠B＝45°，则∠C的度数为（ ）A、35° B、40° C、45° D、50°2. 在Rt△ABC中，斜边AB的长为5，则斜边上的中线CD是（ ）A、2.5 B、5 C、7.5 D、103. 下列图形既属于轴对称图形，又属于中心对称图形的是（ ）A、平行四边形 B、菱形 C、等边三角形 D、正五边形4. 下列各组线段中，能够组成直角三角形的一组是（ ）A、1，2，3 B、2，2，4 C、3，4，5 D、6，7，85. 下列命题中，真命题是（ ）A、对角线互相垂直的矩形是正方形 B、对角线互相垂直且相等的四边形是菱形 C、有三条边相等的四边形是菱形 D、对角线互相垂直且相等的四边形是矩形6. 如图，平行四边形中，对角线 ， 交于点O，点E是的中点.若 ， 则的长为（ ）
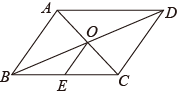A、 B、 C、 D、7. 如图，菱形ABCD的周长为16，对角线AC与BD相交于点O，OE⊥AB，垂足为E，若∠ADC＝120°，则OE的长为（ ）
A、 B、 C、1 D、28. 如图点 在 内，且到三边的距离相等.若 ，则 等于（ ）
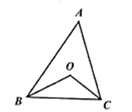A、 B、 C、 D、9. 在 中，∠A∶∠B∶∠C∶∠D可能是（ ）A、1∶2∶2∶1 B、1∶2∶3∶4 C、2∶1∶1∶2 D、2∶1∶2∶110. 如图，已知□ABCD的对角线BD=4cm，将□ABCD绕其对称中心O旋转180°，则点D所转过的路径长为（ ）
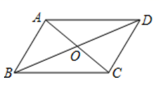A、4π cm B、3π cm C、2π cm D、π cm11. 如图，在中， ， ， ， 点为斜边AB上一动点，过点作于点E，于 ， 连接 ， 则线段的长的最小值为（ ）
A、 B、 C、 D、512. 如图，在正方形ABCD外取一点E，连接AE，BE，DE.过点A作AE的垂线交DE于点P.若AE＝AP＝1，PB＝ ， 下列结论：①△APD≌△AEB；②点B到直线AE的距离为2；③BP＝PD；④S△APD+S△APB＝.其中正确结论的序号是（ ）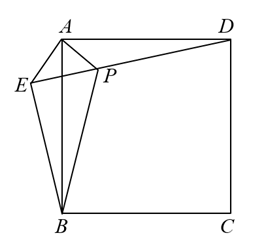
A、①③④ B、①②③ C、②③④ D、①②④二、填空题
-
13. 在Rt△ABC中，∠C=90°，若a=3，b=4，则c=.14. 八边形的内角和为度．15. 如图， ABCD的一个外角为38°，则∠A=度.
16. 菱形的周长为20cm，两个相邻的内角的度数之比为1：2，则较长的对角线长度是cm．17. 把一张矩形纸片（矩形ABCD）按如图方式折叠，使顶点B和点D重合，折痕为EF，若AB＝3cm，BC＝5cm，则重叠部分△DEF的面积为cm2。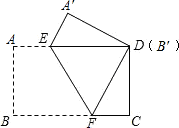
18. 如图，四边形ABCD为菱形，AB=3，∠ABC=60°，点M为BC边上一点且BM=2CM，过M作MNAB交AC，AD于点O，N，连接BN.若点P，Q分别为OC，BN的中点，则PQ的长度为.
三、解答题
-
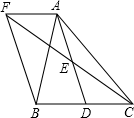
19. 已知某多边形的内角和与外角和的总和为1080°，求此多边形的边数.20. 如图，在△ABC中，边BC＝30，点D在边AB上，BD＝18，连接CD，CD＝24，当AD＝CD时，求AC的长.
21. 如图，点E，F在平行四边形ABCD的边BC，AD上，AF＝CE，连接BF，DE.求证：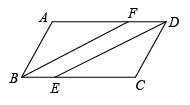
(1)、△ABF≌△CDE；(2)、四边形BEDF是平行四边形.22. 如图，已知线段 ， 求作直角三角形，使一直角边为 ， 斜边为2.（保留作图痕迹，不写作法）
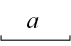23. 如图，在△ABC中，∠C＝90°，AD平分∠BAC，DE⊥AB于点E，点F在AC上，且BD＝DF.求证：
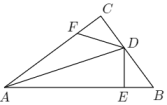(1)、CF＝EB；(2)、AF+EB＝AE.24. 如图，在▱ABCD中，各内角的平分线相交于点E，F，G，H.
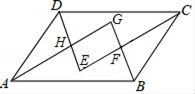(1)、求证：四边形EFGH是矩形；(2)、若AB=6，BC=4，∠DAB=60°，求四边形EFGH的面积.
