苏科版常考题微专练：单项式与多项式的乘法（七年级第二学期数学复习）

试卷更新日期：2023-04-18 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列运算错误的是（）

A、 ${(3 a)}^{2} = 6 a^{2}$ B、 $2 a \cdot 3 a = 6 a^{2}$ C、 $x^{3} \div x^{2} = x$ D、 $- x + 2 x = x$

查看试题解析
2. 下列式子，计算结果为 $x^{2} + 4 x - 21$ 的是（）

A、 $(x + 7) (x - 3)$ B、 $(x - 7) (x + 3)$ C、 $(x + 7) (x + 3)$ D、 $(x - 7) (x - 3)$

查看试题解析
3. 计算 ${(- x y)}^{3} \cdot (7 x y^{2} - 9 x^{2} y)$ 正确的是（）

A、 $- 7 x^{2} y^{5} + 9 x^{3} y^{4}$ B、 $7 x^{2} y^{5} - 9 x^{3} y^{4}$ C、 $- 7 x^{4} y^{5} + 9 x^{5} y^{4}$ D、 $7 x^{4} y^{5} + 9 x^{5} y^{4}$

查看试题解析
4. 若 $(x^{2} + a x + 2) (2 x - 4)$ 的结果中不含 $x$ 项，则 $a$ 的值为（）

A、0 B、2 C、 $\frac{1}{2}$ D、-2

查看试题解析
5. 若 $(x + 2) (2 x - n) = 2 x^{2} + m x + 2$ ，则 $m - n$ 的值是（）

A、6 B、4 C、2 D、 $- 6$

查看试题解析
6. 计算x（y﹣z）﹣y（z﹣x）+z（x﹣y），结果正确的是（）

A、2xy﹣2yz B、﹣2yz C、xy﹣2yz D、2xy﹣xz

查看试题解析
7. 单项式乘以多项式运算法则的依据是（）

A、乘法交换律 B、加法结合律 C、乘法分配律 D、加法交换律

查看试题解析
8. 某同学在计算 $- 3 x^{2}$ 乘一个多项式时错误的计算成了加法，得到的答案是 $x^{2} - x + 1$ ，由此可以推断正确的计算结果是（）

A、 $4 x^{2} - x + 1$ B、 $x^{2} - x + 1$ C、 $- 12 x^{4} + 3 x^{3} - 3 x^{2}$ D、无法确定

查看试题解析
9. 若M=（x-2）（x-7），N=（x-6）（x-3），则M与N的关系为（）

A、M=N B、M＞N C、M＜N D、M与N的大小由x的取值而定

查看试题解析
10. 如图，正方形卡片A类，B类和长方形卡片C类若干张，要拼一个长为（a+mb），宽为（3a+b）的大长方形（m为常数），若知道需用到的B类卡片比A类卡片少1张，则共需C类卡片（）张.

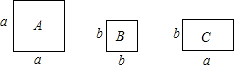A、5 B、6 C、7 D、8

查看试题解析

二、填空题

11. 计算 $3 x \cdot 2 x^{2} y$ 的结果是．

查看试题解析
12. 计算 $4 x \cdot (- 3 x y^{2}) =$ .

查看试题解析
13. 计算 $a (2 a - 1)$ 的结果等于．

查看试题解析
14. 已知 $(x + 4) (x - 9) = x^{2} + m x - 36$ ，则 $m$ 的值为．

查看试题解析
15. 若（x+2m）（x﹣4）去括号后不含x的一次项，则m的值为．

查看试题解析
16. 若多项式 $(x + m)$ 与 $(x + 1)$ 乘积的结果中不含 $x$ 的一次项，则m=.

查看试题解析
17. 对于任意的x、y，若存在a、b使得8x+y（a﹣2b）＝ax﹣2b（x﹣2y）恒成立，则a+b＝.

查看试题解析
18. 一个长方体的长、宽、高分别是3x-4，2x和x，它的体积等于

查看试题解析

三、计算题

19. 计算.

(1)、 $- 1^{2018} + {(π - 3)}^{0} + {(\frac{1}{2})}^{- 1}$

(2)、 $- 6 a b (2 a^{2} b - a b^{2})$

查看试题解析
20. 计算：

(1)、 $m^{3} \cdot m \cdot {(m^{2})}^{3}$ ；

(2)、 $(a + 9) (a + 1)$ ．

查看试题解析
21.

(1)、若3^m=6，3ⁿ=2，求3^2m-3n+1的值.

(2)、已知x²-3x-1=0，求代数式(x-1)(3x+1)-(x+2)²+5的值.

查看试题解析
22. 计算

(1)、（－t）⁵÷（－t）³·（－t）²；

(2)、（2a－b）（a－2b）.

查看试题解析

四、解答题

23. 若单项式 $\frac{1}{3}$ xⁿ⁺¹y与单项式3xyz乘积的结果是一个六次单项式，求n的值．

查看试题解析
24. 已知多项式 $(x^{2} + p x + q) (x^{2} - 3 x + 2)$ 的结果中不含 $x^{3}$ 项和 $x^{2}$ 项，求 $p$ 和 $q$ 的值.

查看试题解析
25. 已知 $(x + a) (x - 2)$ 的结果中不含关于字母 $x$ 的一次项.先化简，再求： ${(a + 1)}^{2} + (2 - a) (2 + a)$ 的值.

查看试题解析
26. 计算：
（1）（﹣5x²y²）•（ $\frac{1}{2}$ x²yz）；
（2）（﹣ $\frac{1}{2}$ ab²c）•（﹣ $\frac{4}{3}$ a²bc²）；
（3）（2x²y）•（﹣x²y²）•（ $\frac{1}{2}$ y²）

查看试题解析
27. 若 $(x + 3 p) (x^{2} - x + \frac{1}{3} q)$ 的积中不含x项与 $x^{2}$ 项

(1)、求p、q的值；

(2)、求代数式 $p^{2019} q^{2020}$ 的值

查看试题解析
28. 借助表格进行多项式乘多项式运算，可以方便合并同类项得出结果，下面尝试利用表格试一试：
例题：（a＋b）（a－b）
解：填表

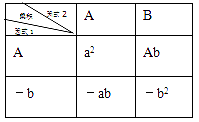
则（a＋b）（a－b）＝a²－b².
根据所学完成下列问题：

(1)、如表，填表计算（x＋2）（x²－2x＋4），（m＋3）（m²－3m＋9），直接写出结果.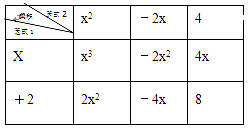
结果为；

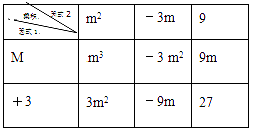
结果为

(2)、根据以上获得的经验填表：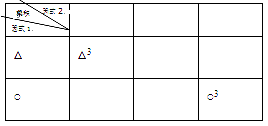
结果为 △³ ＋ ○³ ，根据以上探索，请用字母a、b来表示发现的公式为．

(3)、用公式计算：（2x＋3y）（4x²－6xy＋9y²）＝；
因式分解：27m³－8n³＝．

查看试题解析