苏科版常考题微专练：多边形的内角和和外角和（七年级第二学期数学复习）
试卷更新日期：2023-04-18 类型：复习试卷
一、单选题（每题3分，共24分）
-
1. 一个多边形的内角和的度数可能是（ ）A、1700° B、1800° C、1900° D、2000°2. 一个多边形的外角和是360°，这个多边形是（ ）A、四边形 B、五边形 C、六边形 D、不确定3. 从一个十边形的某个点出发，分别连接这个顶点与其余各顶点，可以把这个多边形分割成三角形（ ）A、10个 B、9个 C、8个 D、7个4. 若从一个多边形的一个顶点出发，最多可以引10条对角线，则它是( )A、十三边形 B、十二边形 C、十一边形 D、十边形5. 若△ABC三个角的大小满足条件∠A：∠B：∠C＝1：3：4，则∠C的大小为（ ）A、22.5° B、45° C、67.5° D、90°6. 如图BE是△ABC的外角∠CBD的平分线，且BE交AC的延长线于点E．若∠A=30°，∠E=20°，则∠ACB的度数是（ ）
A、50° B、60° C、70° D、80°7. 如图，将三角尺的直角顶点放在直尺的一边上，∠1=30°，∠2=50°，则∠3的度数为（ ）
A、 B、 C、 D、8. 如图，将三角形纸片ABC沿DE折叠，当点A落在四边形BCDE的外部时，测量得∠1＝70°，∠2＝152°，则∠A为（ ）
A、40° B、42° C、30° D、52°二、填空题（每空4分，共28分）
-
9. 若多边形的内角和比外角和大540°，则该多边形的边数是 ．10. 五边形的外角和等于 ．11. 如图所示，求∠A＋∠B＋∠C＋∠D＋∠E＋∠F＝ .
12. 如图，直线AB、CD相交于点O，∠BOC＝α，点F在直线AB上且在点O的右侧，点E在射线OC上，连接EF，直线EM、FN交于点G．若∠MEF＝n∠CEF，∠NFE＝（1﹣2n）∠AFE，且∠EGF的度数与∠AFE的度数无关，则∠EGF= ． （用含有α的代数式表示）
13. 如图，.
14. 如图，△ABC中，∠ABC、∠ACB的三等分线交于点E、D，若∠BFC＝120°，∠BGC＝102°，则∠A的度数为
15. 如图，铅笔放置在△ABC的边AB上，笔尖方向为点A到点B的方向，把铅笔依次绕点A、点C、点B按逆时针方向旋转∠A、∠C、∠B的度数后，笔尖方向变为点B到点A的方向，这种变化说明 ．
三、解答题（共9题，共68分）
-
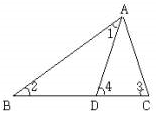
16. 一个多边形的外角和是内角和的 ，求这个多边形的边数及这个多边形共有几条对角线.17. 一个多边形的内角和比它的外角和的4倍多180°，求这个多边形的边数和它的内角和.18. 在△ABC中，∠1=∠2，∠3=∠4，∠BAC=54°，求∠DAC的度数.
19. 将一副直角三角尺 和 如图放置，其中 ， ， ，若 ，试判断 与 的位置关系，并说明理由.
20. 如图，在△ABC中，∠B＝36°，∠C＝76°，AD是△ABC的角平分线，BE是△ABD中AD边上的高，求∠ABE的度数．
21.
(1)、光线从空气中射入水中会产生折射现象，同时光线从水中射入空气中也会产生折射现象，如图1，光线a从空气中射入水中，再从水中射入空气中，形成光线b，根据光学知识有∠1＝∠2，∠3＝∠4，请判断光线a与光线b是否平行，并说明理由；(2)、如图2，直线EF上有两点A、C，分别引两条射线AB、CD．已知∠BAF＝150°，∠DCF＝80°，射线AB、CD分别绕点A、点C以1度/秒和3度/秒的速度同时顺时针转动，设时间为t秒，当射线CD转动一周时，两条射线同时停止．则当直线CD与直线AB互相垂直时，t＝秒．22. 直线MN与直线PQ垂直相交于O，点A在射线OP上运动，点B在射线OM上运动．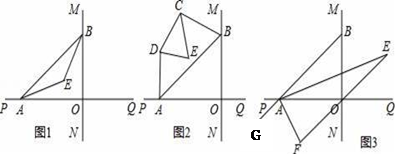
(1)、如图1，已知AE、BE分别是∠BAO和∠ABO角的平分线，点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出∠AEB的大小．(2)、如图2，已知AB不平行CD，AD、BC分别是∠BAP和∠ABM的角平分线，又DE、CE分别是∠ADC和∠BCD的角平分线，点A、B在运动的过程中，∠CED的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值．(3)、如图3，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F，在△AEF中，如果有两个角度数的比是3：2，请直接写出∠ABO的度数 ．23. 探究与发现：(1)、：我们知道，三角形的一个外角等于与它不相邻的两个内角的和.那么，三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢？
已知：如图1，∠FDC与∠ECD分别为△ADC的两个外角，试探究∠A与∠FDC+∠ECD的数量关系.
(2)、三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系？已知：如图2，在△ADC中，DP、CP分别平分∠ADC和∠ACD，试探究∠P与∠A的数量关系.
(3)、若将△ADC改为任意四边形ABCD呢？已知：如图3，在四边形ABCD中，DP、CP分别平分∠ADC和∠BCD，试利用上述结论探究∠P与∠A+∠B的数量关系.
(4)、若将上题中的四边形ABCD改为六边形ABCDEF（图4）呢？请直接写出∠P与∠A+∠B+∠E+∠F的数量关系：.
24. 我们知道：光线反射时，反射光线、入射光线和法线在同一平面内，反射光线、入射光线分别在法线两侧，反射角等于入射角．如图1，EF为一镜面，AO为入射光线，入射点为点O，ON为法线（过入射点O且垂直于镜面EF的直线），OB为反射光线，此时反射角∠BON等于入射角∠AON．
(1)、如图1，若∠AOE=65°，则∠BOF=°；若∠AOB=80°，则∠BOF= °；(2)、两平面镜OP、OQ相交于点O，一束光线从点A出发，经过平面镜两次反射后，恰好经过点B．①如图2，当∠POQ为多少度时，光线？请说明理由．
②如图3，若两条光线AM、NB相交于点E，请探究∠POQ与∠MEN之间满足的等量关系，并说明理由．
③如图4，若两条光线AM、NB所在的直线相交于点E，∠POQ与∠MEN之间满足的等量关系是 ▲ （直接写出结果）