苏科版常考题微专练:平行线的判定与性质(七年级第二学期数学复习)
试卷更新日期:2023-04-18 类型:复习试卷
一、单选题(每题3分,共30分)
-
1. 如图,不能推出的条件是( )
 A、 B、 C、 D、2. 如图,弯形管道ABCD的拐角∠ABC=120°,要保证管道 , 则∠BCD等于( )
A、 B、 C、 D、2. 如图,弯形管道ABCD的拐角∠ABC=120°,要保证管道 , 则∠BCD等于( ) A、60° B、50° C、70° D、65°3. 若∠1与∠2的关系是同位角,∠1=30°,则∠2=( )A、30° B、150° C、50°或130° D、不确定4. 如图,已知a∥b,∠1=75°,则∠2的度数是( )
A、60° B、50° C、70° D、65°3. 若∠1与∠2的关系是同位角,∠1=30°,则∠2=( )A、30° B、150° C、50°或130° D、不确定4. 如图,已知a∥b,∠1=75°,则∠2的度数是( ) A、35° B、75° C、105° D、125°5. 如图,AB∥CD,BC平分∠ABD,若∠1=65°,则∠2的度数是( )
A、35° B、75° C、105° D、125°5. 如图,AB∥CD,BC平分∠ABD,若∠1=65°,则∠2的度数是( )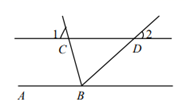 A、65° B、60° C、55° D、50°6. 如图,下列条件能判断AB∥CD的是( )
A、65° B、60° C、55° D、50°6. 如图,下列条件能判断AB∥CD的是( ) A、∠1=∠3 B、∠2=∠3 C、∠1=∠4 D、∠2=∠47. 如图,下列推理中正确的是( )
A、∠1=∠3 B、∠2=∠3 C、∠1=∠4 D、∠2=∠47. 如图,下列推理中正确的是( )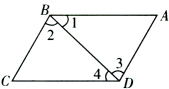 A、∵∠1=∠4,∴BC//AD B、∵∠2=∠3,∴AB//CD C、∵∠BCD+∠ADC=180°,∴AD//BC D、∵∠CBA+∠C=180°,∴BC//AD8. 如图, ,若 , , , 则下列说法正确的是( )
A、∵∠1=∠4,∴BC//AD B、∵∠2=∠3,∴AB//CD C、∵∠BCD+∠ADC=180°,∴AD//BC D、∵∠CBA+∠C=180°,∴BC//AD8. 如图, ,若 , , , 则下列说法正确的是( ) A、 B、 C、 D、9. 如图,直线 , 将含30°角的直角三角板ABC的直角顶点C放在直线b上,若 , 则的度数为( )
A、 B、 C、 D、9. 如图,直线 , 将含30°角的直角三角板ABC的直角顶点C放在直线b上,若 , 则的度数为( ) A、35° B、45° C、55° D、65°10. 如图,小明用两块同样的三角板,按下面的方法做出了平行线,则AB∥CD的理由是( )
A、35° B、45° C、55° D、65°10. 如图,小明用两块同样的三角板,按下面的方法做出了平行线,则AB∥CD的理由是( ) A、∠2=∠4 B、∠3=∠4 C、∠5=∠6 D、∠2+∠3+∠6=180°
A、∠2=∠4 B、∠3=∠4 C、∠5=∠6 D、∠2+∠3+∠6=180°二、填空题(每题3分,共24分)
-
11. 如图,木工用角尺画出 , 其依据是 .
 12. 如图 , CB平分 , 则的度数为 .
12. 如图 , CB平分 , 则的度数为 .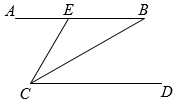 13. 如图所示,请添加一个条件,使AB//CE.则添加的条件为.
13. 如图所示,请添加一个条件,使AB//CE.则添加的条件为.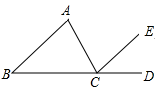 14. 如图,若ABCDEF,则∠x,∠y,∠z三者之间的数量关系是.
14. 如图,若ABCDEF,则∠x,∠y,∠z三者之间的数量关系是. 15. 如图, , , 若∠B=72°,则∠D的度数是.
15. 如图, , , 若∠B=72°,则∠D的度数是.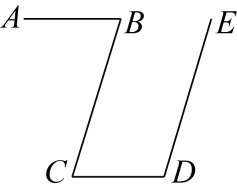 16. 一副三角板按如图所示(共顶点A)叠放在一起,若固定三角板AOB,改变三角板ACD的位置(其中A点位置始终不变),则当∠BAD=°时,.
16. 一副三角板按如图所示(共顶点A)叠放在一起,若固定三角板AOB,改变三角板ACD的位置(其中A点位置始终不变),则当∠BAD=°时,.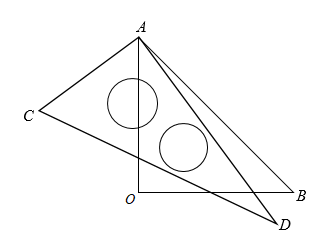 17. 如图,直线、被直线所截,交点分别为M、N,则的同位角是.
17. 如图,直线、被直线所截,交点分别为M、N,则的同位角是.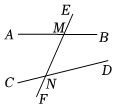 18. 如图,与 是内错角的是.
18. 如图,与 是内错角的是.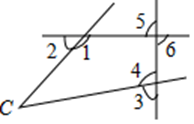
三、解答题(共8题,共66分)
-
19. 根据下列推理进行填空:
已知:如图,点 在 上,且 平分 , .求证: .
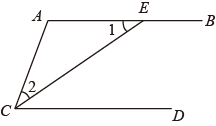
证明:∵ 平分 (已知)
∴ __▲_( )
又∵ ( )
∴ _▲( )
∴ ( )
20. 完成下面的证明过程.已知:如图,点E、F分别在AB、CD上,AD分别交EC、BF于点H、G,∠1=∠2,∠B=∠C.求证∠A=∠D.

证明:∵∠1=∠2(已知),
∠2=∠AGB( ),
∴∠1= .
∴EC∥BF( ).
∴∠B=∠AEC( ).
又∵∠B=∠C(已知),
∴∠AEC= .
∴ ( ).
∴∠A=∠D( ).
21. 已知:如图,∠BAE+∠AED=180°,∠1=∠2,∠M和∠N有怎样的数量关系,并说明理由. 22. 如图,AB//CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AD//BC.
22. 如图,AB//CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AD//BC. 23. 如图,在△ABC中,E、G分别是AB、AC上的点,F、D是BC上的点,连接EF、AD、DG,ADEF,∠1+∠2=180°.
23. 如图,在△ABC中,E、G分别是AB、AC上的点,F、D是BC上的点,连接EF、AD、DG,ADEF,∠1+∠2=180°. (1)、说明:ABDG;(2)、若∠2=145°,∠B=35°,说明:DG是∠ADC的平分线.24. 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
(1)、说明:ABDG;(2)、若∠2=145°,∠B=35°,说明:DG是∠ADC的平分线.24. 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F. (1)、CD与EF平行吗?请说明理由;(2)、如果∠1=∠2,且∠3=110°,求∠ACB的度数.25. 如图1,已知直线AB//CD,∠A=∠C=100°.
(1)、CD与EF平行吗?请说明理由;(2)、如果∠1=∠2,且∠3=110°,求∠ACB的度数.25. 如图1,已知直线AB//CD,∠A=∠C=100°. (1)、试判断直线AD和BC的位置关系?并说明理由;(2)、如图2若E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF,是否存在∠BEC=∠ADB?如果存在,请求出∠ADB的度数,如果不存在,请说明理由.
(1)、试判断直线AD和BC的位置关系?并说明理由;(2)、如图2若E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF,是否存在∠BEC=∠ADB?如果存在,请求出∠ADB的度数,如果不存在,请说明理由.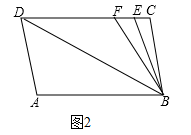 26. 如图
26. 如图 (1)、光线从空气中射入水中会产生折射现象,同时光线从水中射入空气中也会产生折射现象,如图1,光线a从空气中射入水中,再从水中射入空气中,形成光线b,根据光学知识有∠1=∠2,∠3=∠4,请判断光线a与光线b是否平行,并说明理由.(2)、光线照射到镜面会产生反射现象,由光学知识,入射光线与镜面的夹角与反射光线与镜面的夹角相等,如图2有一口井,已知入射光线a与水平线OC的夹角为36°,问如何放置平面镜MN,可使反射光线b正好垂直照射到井底?(即求MN与水平线的夹角)(3)、如图3,直线EF上有两点A、C,分别引两条射线AB、CD.∠BAF=110°,∠DCF=50°,射线AB、CD分别绕A点,C点以1度/秒和3度/秒的速度同时顺时针转动,设时间为t,在射线CD转动一周的时间内,当t= , 使得CD与AB平行.
(1)、光线从空气中射入水中会产生折射现象,同时光线从水中射入空气中也会产生折射现象,如图1,光线a从空气中射入水中,再从水中射入空气中,形成光线b,根据光学知识有∠1=∠2,∠3=∠4,请判断光线a与光线b是否平行,并说明理由.(2)、光线照射到镜面会产生反射现象,由光学知识,入射光线与镜面的夹角与反射光线与镜面的夹角相等,如图2有一口井,已知入射光线a与水平线OC的夹角为36°,问如何放置平面镜MN,可使反射光线b正好垂直照射到井底?(即求MN与水平线的夹角)(3)、如图3,直线EF上有两点A、C,分别引两条射线AB、CD.∠BAF=110°,∠DCF=50°,射线AB、CD分别绕A点,C点以1度/秒和3度/秒的速度同时顺时针转动,设时间为t,在射线CD转动一周的时间内,当t= , 使得CD与AB平行.