浙江省常考题微专练：整式的混合运算（七年级第二学期数学复习）

试卷更新日期：2023-04-18 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列等式正确的是（）

A、 $- a (1 + a^{2}) = - a + a^{3}$ B、 $2 (a - 2 b) = 2 a - 2 b$ C、 ${(m - 2)}^{2} = m^{2} - 4$ D、 ${(a - 1)}^{2} = a^{2} - 2 a + 1$

查看试题解析
2. 已知 $(- x) (2 x^{2} - a x - 1) - 2 x^{3} + 3 x^{2}$ 中不含 $x$ 的二次项，则 $a$ 的值是（）

A、3 B、2 C、-3 D、-2

查看试题解析
3. 已知：x﹣3y＝4，那么代数式x﹣3y﹣3（y﹣x）﹣2（x﹣3）的值为（）

A、12 B、13 C、14 D、16

查看试题解析
4. 要使等式（x-2y）²+A=（x+2y）²成立，代数式A应是（）

A、4xy B、-4xy C、8xy D、-8xy

查看试题解析
5. 下面四个整式中，不能表示图中阴影部分面积的是（）

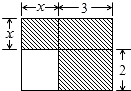A、x²+5x B、（x+3）（x+2）﹣2x C、3（x+2）+x² D、x（x+3）+6

查看试题解析
6. 用如图所示的正方形和长方形卡片若干张，拼成一个长为 $3 a + 2 b$ ，宽为 $a + b$ 的长方形，需要 $B$ 类卡片（）张.

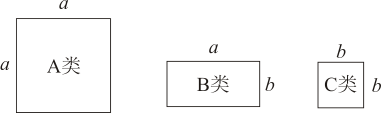A、3 B、4 C、5 D、6

查看试题解析
7. 互不重合的A，B，C三点在同一直线上，已知AC=2a+1，BC=a+4，AB=3a，这三点的位置关系是（）

A、点A在B，C两点之间 B、点B在A，C两点之间 C、点C在A，B两点之间 D、无法确定

查看试题解析
8. 某天数学课上，老师讲了单项式乘多项式，放学回到家，小明拿出课堂笔记复习，发现一道题：- $3 x y (4 y - 2 x -$ $1) = - 12 x y^{2} + 6 x^{2} y + □ ， □$ 的地方被钢笔水弄污了，你认为 $□$ 内应填写（）

A、3xy B、 $- 3 x y$ C、-1 D、1

查看试题解析
9. 某厂原来生产一种边长为a厘米的正方形地砖，现将地砖的一边扩大3厘米，另一边缩短3厘米，改成生产长方形地砖.若材料的成本价为每平方厘米b元，则这种长方形地砖每块的材料成本价与正方形地砖相比（）

A、增加了9b元 B、增加了3ab元 C、减少了9b元 D、减少了3ab元

查看试题解析
10. 将大小不一的正方形纸片①、②、③、④放置在如图所示的长方形ABCD内（相同纸片之间不重叠），其中AB＝a.小明发现：通过边长的平移和转化，阴影部分⑤的周长与正方形①的边长有关，那么阴影部分⑥与阴影部分⑤的周长之差与正方形（）（填编号）的边长有关.

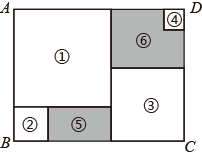A、① B、② C、③ D、④

查看试题解析

二、填空题

11. 已知x²﹣3x＝2，那么多项式x³﹣x²﹣8x+9的值是．

查看试题解析
12. 已知 $x y^{2} = - 2$ ，则 $- x y (x^{2} y^{5} - x y^{3} - y)$ 的值为.

查看试题解析
13. 已知实数a²＋b²＝7，a＋b＝3，则（a﹣2）（b﹣2）＝.

查看试题解析
14. 若m²＝n+2020，n²＝m+2020（m≠n），那么代数式m³﹣2mn+n³的值．

查看试题解析
15. 已知某三角形第一条边长为 $（ 3 a - 2 b ）$ cm，第二条边比第一条边长 $（ a + 2 b ）$ cm，第三条边比第一条边的2倍少bcm，则这个三角形的周长为cm．

查看试题解析
16. 小亮用边长为a的正方形纸片，边长为b的正方形纸片，及边长分别为a和b的长方形纸片，各若干张，拼出了邻边长分别为3a+b和4a+3b的大长方形，那么小亮用了三种纸片一共张.

查看试题解析

三、解答题

17. 计算：

(1)、 ${(- 1)}^{2022} + {(- \frac{1}{2})}^{- 2} - {(3.14 - π)}^{0}$

(2)、4x³ ÷（-2x）²-（2x²-x）÷（ $\frac{1}{2}$ x）

查看试题解析
18. 计算与化简：

(1)、 ${(- \frac{1}{2})}^{- 3} + {(π - \sqrt{2})}^{0}$ ；

(2)、（-2t²)³+(-3t³)²；

(3)、(2m-3n)(3n-2m)-(2m-3n)(3n+2m)

查看试题解析
19.

(1)、先化简，再求值： $m (m - 2 n) + {(m + n)}^{2} - (m + n) (m - n)$ ，其中 $m = - 1$ ， $n = 4$ ；

(2)、已知 $x + y = 3$ ， $x y = 2$ ，求 ${(x - y)}^{2}$ 的值．

查看试题解析
20. 先化简，再求值： ${(2 x + y)}^{2} + (2 x + y) (2 x - y) - 8 x^{2}$ ，其中 $x = - 3$ ， $y = \frac{1}{2}$ .

查看试题解析
21. 先化简，后求值： $(2 x + 3) (2 x - 3) - {(x - 2)}^{2} - 4 x (x - 1)$ ，其中 $x = 2$ .

查看试题解析
22. 先化简，再求值： $(x + 1) (x - 1) + x (2 - x) + {(x - 1)}^{2}$ ，其中 $x = 100$

查看试题解析
23. 先化简，再求值：(2a－3b)²－(2a＋3b)(2a－3b)＋6b(a-3b).其中a= $-$ 6，b= $\frac{1}{2}$ .

查看试题解析
24. 先化简，再求值： $(2 m + 3) \cdot (2 m - 3) - {(m - 1)}^{2} + {(2 m)}^{3} \div (- 8 m)$ ，其中 $m$ 满足 $m^{2} + m - 2 = 0.$

查看试题解析
25.

(1)、化简：（a+2b）²+（2a+b）（2a-b）-4b（a+b）；

(2)、设b = ma，是否存在实数m，使得（a+2b）²+（2a+b）（2a-b）-4b（a+b）能化简为2a² ，若能，请求出满足条件的m值；若不能，请说明理由.

查看试题解析
26. 先化简，再求值.

(1)、 $(2 x + y) (2 x - y) - 4 x (x - y)$ ，其中 $x = \frac{1}{2} ， y = - 1$ ；

(2)、已知 $x^{2} - 3 x + 2 = 0$ ，求代数式 $(x - 1) (3 x + 1) - {(x + 2)}^{2} + 5$ 的值；

(3)、已知 $x^{3 m} = 2 ， y^{2 m} = 3$ ，求 ${(x^{2 m})}^{3} + {(y^{m})}^{6} - {(x^{2} y)}^{3 m} \cdot y^{m}$ 的值.

查看试题解析