浙江省常考题微专练：平方差公式（七年级第二学期数学复习）

试卷更新日期：2023-04-18 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列算式可用平方差公式的是（）

A、（n+2m）(m-2n) B、（-m-n）(m+n) C、（-m-n）(m-n) D、（m-n）(-m+n)

查看试题解析
2. 下列各式不能使用平方差公式的是（）

A、 $(2 a + 3 b) (2 a - 3 b)$ B、 $(2 a - 3 b) (- 2 a - 3 b)$ C、 $(- 2 a + 3 b) (- 2 a - 3 b)$ D、 $(- 2 a + 3 b) (3 b - 2 a)$

查看试题解析
3. 下列各式，不能用平方差公式计算的是（）

A、 $(x + 2 y) (x - 2 y)$ B、 $(- x - 2 y) (2 y - x)$ C、 $(x - 2 y) (x + 3 y)$ D、 $(2 x + y + 3) (2 x + y - 3)$

查看试题解析
4. 下列多项式中能用平方差公式分解因式的是（）

A、 $x^{2} + y^{2}$ B、 $- a^{2} - b^{2}$ C、 $x^{3} - y^{2}$ D、 $a^{2} - b^{2}$

查看试题解析
5. 若 $a + b = 3$ ，则 $a^{2} + 6 b - b^{2}$ 的值为（）

A、3 B、6 C、9 D、12

查看试题解析
6. 计算（a﹣b）（a+b）（a²﹣b²）的结果是（）

A、a⁴﹣2a²b²+b⁴ B、a⁴+2a²b²+b⁴ C、a⁴+b⁴ D、a⁴﹣b⁴

查看试题解析
7. 一个长方形的长为2x﹣y，宽为2x+y，则这个长方形的面积是（）

A、4x²﹣y² B、4x²+y² C、2x²﹣y² D、2x²+y²

查看试题解析
8. 对于任意整数 n，多项式 ${(n + 7)}^{2} - {(n - 3)}^{2}$ 的值都能（）

A、被20整除 B、被7整除 C、被21整除 D、被 $n + 4$ 整除

查看试题解析
9. 已知 $M = 2022^{2} ， N = 2021 \times 2023$ ，则 $M$ 与 $N$ 的大小关系是（）

A、 $M > N$ B、 $M < N$ C、 $M = N$ D、不能确定

查看试题解析
10. 化简 $(2 + 1) (2^{2} + 1) (2^{4} + 1) (2^{8} + 1) (2^{16} + 1)$ 的结果是（）

A、 $2^{32} - 1$ B、 $2^{32} + 1$ C、 ${(2^{16} + 1)}^{2}$ D、 ${(2^{16} - 1)}^{2}$

查看试题解析

二、填空题

11. 计算 $① (2 x + y) (2 x - y) =$ ； $② {(2 x + 3 y)}^{2} =$ .

查看试题解析
12. 若 $m^{2} - n^{2} = 6$ ， m+n＝3，则 $\frac{m - n}{2}$ ＝.

查看试题解析
13. 若 $x + y + z = 2 ， x^{2} - {(y + z)}^{2} = 8$ ，则 $x - y - z$ =.

查看试题解析
14. 已知 $4 m^{2} - 9 n^{2} = 26 ， 2 m + 3 n = 13$ ，则 $2 m - 3 n =$ .

查看试题解析
15. 若 $a + b = 4 ， a - b = 1$ ，则 ${(a + 1)}^{2} - {(b - 1)}^{2}$ 的值为.

查看试题解析
16. 已知 ${\begin{cases} x = a \\ y = b \end{cases}$ 是方程组 ${\begin{cases} 2 x - 3 y = - 2 \\ 2 x + 3 y = 7 \end{cases}$ 的解，则代数式4a²-9b²的值

查看试题解析

三、综合题

17. 计算：

(1)、 $a^{6} - {(a^{2})}^{3} - {(- 2 a^{3})}^{2}$ ；

(2)、 $(y + 2) (y - 2) - 2 (y - 1)$ ．

查看试题解析
18.

(1)、已知a+b＝5，ab＝ $- \frac{1}{4}$ ，求下列各式的值：
①a²+b²； ②（a﹣b）².

(2)、若2x+3y﹣4z+1＝0，求9^x•27^y÷81^z的值.

查看试题解析
19. 先化简，再求值： $(2 x + 5) (2 x - 5) + {(x - 3)}^{2} - 6 x (x - 1)$ ，其中 $x = 6$ .

查看试题解析
20. 阅读材料：已知 $a + b = - 4$ ， $a b = 3$ ，求 $a^{2} + b^{2}$ 的值.
∵ $a + b = - 4$ ， $a b = 3$ ，
∴ $a^{2} + b^{2} = {(a + b)}^{2} - 2 a b = {(- 4)}^{2} - 2 × 3 = 10$ .
请你参考上述材料解答下面问题：

(1)、已知 $a - b = 6$ ， $a b = - 2$ ，求 $a^{2} + b^{2}$ 的值.

(2)、已知 $x + y = 6$ ，求 $x^{2} - y^{2} + 12 y$ 的值.

查看试题解析
21. 若x满足(9 $-$ x)(x $-$ 4)=4，求(9 $-$ x)² $+$ (x $-$ 4)²的值.
解：设9 $-$ x=a，x $-$ 4=b，则(9 $-$ x)(x $-$ 4)=ab=4，a $+$ b=(9 $-$ x) $+$ (x $-$ 4)=5
∴(9 $-$ x)² $+$ (x $-$ 4)²=a²+b²=(a+b)² $-$ 2ab=5²—2 $\times$ 4=17

请仿照上面的方法求解下面问题：

(1)、若x满足 $(x - 10) (x - 20) = 15$ ，求 ${(x - 10)}^{2} + {(x - 20)}^{2}$ 的值；

(2)、若x满足 ${(x - 2021)}^{2} + {(x - 2022)}^{2} = 33$ ，求 $(x - 2021) (x - 2022)$ 的值

(3)、已知正方形ABCD的边长为x，E，F分别是AD、DC上的点，且AE=1，CF=3，长方形 EMFD的面积是48，分别以MF，DF为边长作正方形MFRN和正方形GFDH，求阴影部分的面积.

查看试题解析
22. 如图1，边长为 $a$ 的大正方形有一个边长为 $b$ 的小正方形，把图1中的阴影部分拼成一个长方形（如图2所示）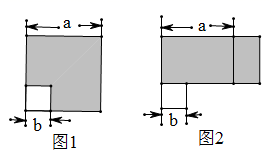

(1)、如图1，可以求出阴影部分的面积是（写成平方差的形式）

(2)、如图2，若将阴影部分裁剪下来，重新拼成一个长方形，它的宽是，长是，面积是.（写成多项式乘法形式）

(3)、比较左、右两图的阴影部分面积，可以得到公式.

(4)、请应用这个公式完成下列各题：
①已知 $4 m^{2} - n^{2} = 12$ ， $2 m + n = 4$ ，则 $2 m - n =$

②计算： $202 0^{2} - 2018 \times 2022$ =

③计算： $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) ⋯ (1 - \frac{1}{201 9^{2}}) (1 - \frac{1}{202 0^{2}})$

查看试题解析

浙江省常考题微专练： 平方差公式（七年级第二学期数学复习）

一、单选题

二、填空题

三、综合题

浙江省常考题微专练：平方差公式（七年级第二学期数学复习）