浙江省常考题微专练: 完全平方公式(七年级第二学期数学复习)
试卷更新日期:2023-04-18 类型:复习试卷
一、单选题
-
1. 运算结果为2mn﹣m2﹣n2的是()A、(m﹣n)2 B、﹣(m﹣n)2 C、﹣(m+n)2 D、(m+n)22. 若 的值使得 成立,则 的值为( )A、5 B、4 C、3 D、23. 已知a+b=3,ab=2,则 的值是( )A、1 B、4 C、16 D、94. 已知 ,若M=a2-ac,N=ac-c2 , 则M与N的大小关系是( )A、M>N B、M=N C、M<N D、不能确定5. 如图,给出了正方形 的面积的四个表达式,其中错误的是( )
 A、 B、 C、 D、6. 图(1)是一个长为2a,宽为的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )
A、 B、 C、 D、6. 图(1)是一个长为2a,宽为的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( ) A、 B、 C、 D、7. 如图,有甲、乙、丙三种纸片各若干张,其中甲、乙分别是边长为a,b的正方形,丙是长为b,宽为a的长方形.若同时用甲、乙、丙纸片分别为4张、9张、12张拼成正方形,则拼成的正方形的边长为( )
A、 B、 C、 D、7. 如图,有甲、乙、丙三种纸片各若干张,其中甲、乙分别是边长为a,b的正方形,丙是长为b,宽为a的长方形.若同时用甲、乙、丙纸片分别为4张、9张、12张拼成正方形,则拼成的正方形的边长为( ) A、a+2b B、a+3b C、2a+3b D、3a+2b8. 在数学活动课上,一位同学用四张完全一样的长方形纸片(长为 ,宽为 , )搭成如图一个大正方形,面积为132,中间空缺的小正方形的面积为28.下列结论中,正确的有( ).
A、a+2b B、a+3b C、2a+3b D、3a+2b8. 在数学活动课上,一位同学用四张完全一样的长方形纸片(长为 ,宽为 , )搭成如图一个大正方形,面积为132,中间空缺的小正方形的面积为28.下列结论中,正确的有( ).
① ;② ;③ ;④
A、①②③ B、①②④ C、①③④ D、②③④9. 已知长、宽分别为x,y的长方形周长为6,面积为1,则(x-y)2的值为( )A、5 B、7 C、11 D、1310. 如图,为了美化校园,某校要在面积为30平方米长方形空地中划出长方形和长方形 , 若两者的重合部分恰好是一个边长为3米的正方形,现将图中阴影部分区域作为花圃,若长方形空地的长和宽分别为和 , , 花圃区域和总周长为14米,则m-n的值为( )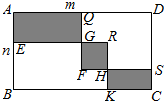 A、米 B、米 C、米 D、米
A、米 B、米 C、米 D、米二、填空题
-
11. 若x2+mx+4=(x+2)2 , 则常数m的值是 .12. 已知 , ,则 的值为.13. 若a-b=7,ab=-12,则(a+b)2=14. 若等式x2+6x+m=(x+3)2-1成立,则常数m的值是 .15. 已知4n+4-n=a,则16n+16-n的值为(用字母a表示).16. 如图,在边长为a(cm)的大正方形内放入三个边长都为b(cm)(a>b)的小正方形纸片,这三张纸片没有盖住的面积是4cm2 , 则a2-2ab+b2的值为.
 17. 已知(2022-a)2+(a-2023)2 = 7,则(2022-a)(a-2023)的值为
17. 已知(2022-a)2+(a-2023)2 = 7,则(2022-a)(a-2023)的值为三、计算题
-
18.(1)、解方程:① ② .(2)、简便计算:19.92+19.9×0.2+0.12.19. 利用乘法公式简便计算:(1)、1002﹣992+982﹣972+…+22﹣12;(2)、1252﹣50×125+252.
四、综合题
-
20. 已知实数a,b满足(a+b)2=9,(a﹣b)2=3,求a2+b2﹣ab的值.21.(1)、化简:.(2)、利用(1)中的结果,计算的值,其中 , , .(3)、若 , , , 求的值.22. 先化简,再求值: ,其中 .23. 如图
 (1)、数学中有很多等式可以用图形的面积来表示.观察上图,直接写出代数式(a+b)2 , (a-b)2 , ab之间的等量关系;(2)、根据(1)题中的等量关系,解决如下问题:
(1)、数学中有很多等式可以用图形的面积来表示.观察上图,直接写出代数式(a+b)2 , (a-b)2 , ab之间的等量关系;(2)、根据(1)题中的等量关系,解决如下问题:①已知m-n = 7,mn=-12.求m+n的值;
②若(6-x)(8+x) = 7,求(6-x)2+(8+x)2的值.
24. 图①是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它平均分成形状和大小都一样的四块小长方形,然后按图②那样拼成一个正方形.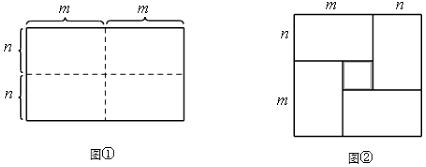 (1)、观察图②,请用两种不同的方法表示图②中阴影部分的面积:
(1)、观察图②,请用两种不同的方法表示图②中阴影部分的面积:方法1:;
方法2:;
(2)、直接写出三个代数式(m+n)2 , (m﹣n)2 , mn之间的等量关系:;(3)、若a+b=7,ab=6,求a﹣b的值.25. 两个边长分别为a、b(a>b)的正方形如图(1)放置,现在取BD的中点P,连接PA、PE,如图(2),把图形分割成三部分,分别标记①、②、③,对应的图形面积分别记为S①、S②、S③.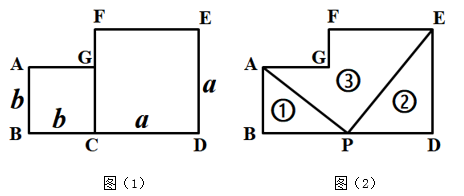 (1)、用字母a、b分别表示S①、S②.(2)、若a-b=2,ab=15,求S①+S②.(3)、若S①+S②=3,ab=1,求S③.26. 若x满足(9 x)(x 4)=4,求(9 x)² (x 4)²的值.
(1)、用字母a、b分别表示S①、S②.(2)、若a-b=2,ab=15,求S①+S②.(3)、若S①+S②=3,ab=1,求S③.26. 若x满足(9 x)(x 4)=4,求(9 x)² (x 4)²的值.解:设9 x=a,x 4=b,则(9 x)(x 4)=ab=4,a b=(9 x) (x 4)=5
∴(9 x)² (x 4)²=a²+b²=(a+b)² 2ab=5²—2 4=17请仿照上面的方法求解下面问题:
 (1)、若x满足 ,求 的值;
(1)、若x满足 ,求 的值;
(2)、若x满足 ,求 的值
(3)、已知正方形ABCD的边长为x,E,F分别是AD、DC上的点,且AE=1,CF=3,长方形 EMFD的面积是48,分别以MF,DF为边长作正方形MFRN和正方形GFDH,求阴影部分的面积.