浙江省常考题微专练: 平行线的判定与性质(七年级第二学期数学复习)
试卷更新日期:2023-04-18 类型:复习试卷
一、单选题
-
1. 如图,已知 , 则( )
 A、 B、 C、 D、2. 如图,直线a,b被直线c所截,下列条件中,不能得到 的 是( )
A、 B、 C、 D、2. 如图,直线a,b被直线c所截,下列条件中,不能得到 的 是( ) A、∠1=∠3 B、∠2=∠4 C、∠3+∠4=180° D、∠1+∠4=180°3. 如图,若 , 要使 , 则需具备另一个条件是( )
A、∠1=∠3 B、∠2=∠4 C、∠3+∠4=180° D、∠1+∠4=180°3. 如图,若 , 要使 , 则需具备另一个条件是( )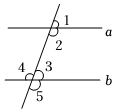 A、 B、 C、 D、4. 如图,能判定直线a∥b的条件是( )
A、 B、 C、 D、4. 如图,能判定直线a∥b的条件是( )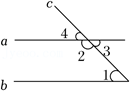 A、∠1=∠2 B、∠3=∠4 C、∠1+∠3=180° D、∠1=∠45. 如图,两只手的食指和拇指在同一平面内,在以下四种摆放方式中,它们构成的一对角可以看成同位角的是( )A、
A、∠1=∠2 B、∠3=∠4 C、∠1+∠3=180° D、∠1=∠45. 如图,两只手的食指和拇指在同一平面内,在以下四种摆放方式中,它们构成的一对角可以看成同位角的是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上,若∠2=65°,则∠1的度数是( )
6. 如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上,若∠2=65°,则∠1的度数是( )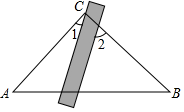 A、15° B、25° C、35° D、65°7. 如图, , 直线分别交、于E、F两点,若 , 则等于( )
A、15° B、25° C、35° D、65°7. 如图, , 直线分别交、于E、F两点,若 , 则等于( )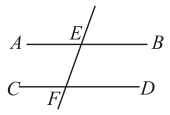 A、 B、 C、 D、8. 如图,已知AB、CD、EF互相平行,且 , EC为的角平分线,则的度数为( )
A、 B、 C、 D、8. 如图,已知AB、CD、EF互相平行,且 , EC为的角平分线,则的度数为( ) A、125° B、55° C、110° D、145°9. 将一个直角三角板和一把直尺按如图所示的方式摆放,若∠2=55°,则∠1的度数为( )
A、125° B、55° C、110° D、145°9. 将一个直角三角板和一把直尺按如图所示的方式摆放,若∠2=55°,则∠1的度数为( ) A、45° B、55° C、25° D、35°10. 如图,有下列判定,其中正确的有( )
A、45° B、55° C、25° D、35°10. 如图,有下列判定,其中正确的有( )①若∠1=∠3,则 AD∥BC;
②若 AD∥BC,则∠1=∠2=∠3;③若∠1=∠3,AD∥BC,则∠1=∠2;
④若∠C+∠3+∠4=180°,则 AD∥BC. A、1 个 B、2 个 C、3 个 D、4 个
A、1 个 B、2 个 C、3 个 D、4 个二、填空题
-
11. 如图,已知 , , ,则 度.
 12. 如图, , ,当 °时, .
12. 如图, , ,当 °时, .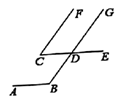 13. 如图表示钉在一起的木条a,b,c.若测得∠1=50°,∠2=75°,要使木条a//b,木条a至少要旋转°.
13. 如图表示钉在一起的木条a,b,c.若测得∠1=50°,∠2=75°,要使木条a//b,木条a至少要旋转°. 14. 如图,木棒AB、CD与EF分别在G、H处可旋转的螺丝铆住,∠EGB=100°,∠EHD=80°,将木棒AB绕点G旋转到与木棒CD平行,则至少要旋转 度.
14. 如图,木棒AB、CD与EF分别在G、H处可旋转的螺丝铆住,∠EGB=100°,∠EHD=80°,将木棒AB绕点G旋转到与木棒CD平行,则至少要旋转 度. 15. 如图,下列条件中能推出a∥b的有.
15. 如图,下列条件中能推出a∥b的有.
①∠3=∠5, ②∠1=∠7,③∠2+∠5=180°,④∠1+∠4=180°.
16. 如图所示,一条街道的两个拐角∠ABC和∠BCD,若∠ABC=150°, 当街道AB和CD平行时,∠BCD=度.
三、解答题
-
17. 如图,EF∥AD,∠DGA+∠BAC=180°,说明:∠1=∠2,请将说明过程填写完成.
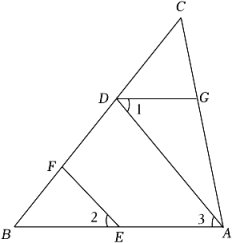
解:∵EF∥AD,(已知)
∴∠2=▲ .( )
∵∠DGA+∠BAC=180°,( )
∴DG∥AB,( )
∴∠1=∠3,( )
∴∠1=∠2.( )
18. 如图是潜望镜示意图,代表镜子.且 , , .求证:.
请补全下述证明过程:
证明:∵ ,
∴ ▲ .
∵ ,
∴.
∵ ,
▲ ,
∴ ▲ .
∴( ).
19. 如图, , 求的度数.请完善其解答过程,并在括号内填写相应的理论依据.
解:∵(已知),
∴ ▲ ▲ ( ),
∴( ),
∵( ),
∴ ▲ .
20. 如图,已知AB∥CD,∠1=∠2.求证:∠E=∠F.
 21. 如图,已知 于点A , 交 于点E , 且 于点F.
21. 如图,已知 于点A , 交 于点E , 且 于点F.
求证: .
证明:∵ 于点A , 于点F , (已知)
∴ . (垂直的定义)
∴ , ( )
∴▲ ( )
∵ ,(已知)
∴ ▲ . (两直线平行,同位角相等)
∵ ,
∴ . (等量代换)
四、综合题
-
22. 如图,已知CFAG,E是直线AB上的一点,CE平分∠ACD,射线CF⊥CE,∠2=58°.
 (1)、求∠ACE的度数;(2)、若∠1=32°,说明:ABCD.23. 如图,AB、CD被AC所截,AB∥CD,∠CAB=108°,点P为直线AB上一动点(不与点A重合),连CP,作∠ACP和∠DCP的平分线分别交直线AB于点E、F.
(1)、求∠ACE的度数;(2)、若∠1=32°,说明:ABCD.23. 如图,AB、CD被AC所截,AB∥CD,∠CAB=108°,点P为直线AB上一动点(不与点A重合),连CP,作∠ACP和∠DCP的平分线分别交直线AB于点E、F.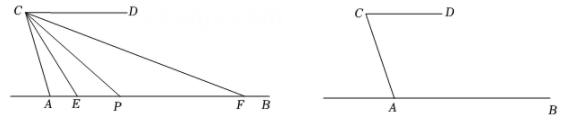 (1)、当点P在点A的右侧时;
(1)、当点P在点A的右侧时;①若∠ACP=36°,则此时CP是否平分∠ECF,请说明理由.
②求∠ECF的度数.
(2)、在点P运动过程中,直接写出∠APC与∠AFC之间的数量关系.24. 数学课上,老师要求同学们利用三角尺画两条平行线. (1)、如图1,小颖用两个含30°的三角尺画出平行线a,b.那么小颖得到 的直接依据是 .(2)、同桌小亮用一个含45°的三角尺和两个含30°的三角尺按如图2方式摆放,并画出平行线a,b.
(1)、如图1,小颖用两个含30°的三角尺画出平行线a,b.那么小颖得到 的直接依据是 .(2)、同桌小亮用一个含45°的三角尺和两个含30°的三角尺按如图2方式摆放,并画出平行线a,b.请帮助小亮完成下面的证明:
由题意得∠ABC=90°,∠1=30°,∠2=60°,过点B作 ,
又∵∠2=60°(已知),∴▲ =∠2=60°( ).
∵∠ABC=90°(已知),∴∠CBD= ▲ °.
又∵∠1=30°(已知),∴∠CBD=∠1(等量代换),
∴▲ ▲ (内错角相等,两直线平行).
∵ ,∴ ( ).
25. 如图 (1)、如图1,点E在BC上,∠A=∠D,∠ACB =∠CED.请说明 AB∥CD 的理由.(2)、如图2,AB∥CD,BG 平分∠ABE,与∠EDF 的平分线交于 H 点,若∠DEB比∠DHB 大60°,求∠DEB 的度数.(3)、保持(2)中所求的∠DEB 的度数不变,如图3,AB∥CD,BM 平分∠EBK,DN 平分∠CDE,作 BP∥DN,则∠PBM 的度数是否改变?若不变,请直接写出∠PBM 的度数;若改变,请说明理由.
(1)、如图1,点E在BC上,∠A=∠D,∠ACB =∠CED.请说明 AB∥CD 的理由.(2)、如图2,AB∥CD,BG 平分∠ABE,与∠EDF 的平分线交于 H 点,若∠DEB比∠DHB 大60°,求∠DEB 的度数.(3)、保持(2)中所求的∠DEB 的度数不变,如图3,AB∥CD,BM 平分∠EBK,DN 平分∠CDE,作 BP∥DN,则∠PBM 的度数是否改变?若不变,请直接写出∠PBM 的度数;若改变,请说明理由.