2023学苏科版数学七年级下学期期中考试模拟卷(2)【范围:第7~9章】
试卷更新日期:2023-04-18 类型:期中考试
一、单选题(每题3分,共24分)
-
1. 下列图案中,能通过左边的图案平移得到的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 下列运算正确的是( )A、 B、 C、 D、3. 下列因式分解正确的是()A、 B、 C、 D、4. 如图,P为△ABC内一点,连接AP、BP、CP并延长分别交边BC、AC、AB于点D、E、F,则把△ABC分成六个小三角形,其中四个小三角形面积已在图上标明,则△ABC的面积为( )
2. 下列运算正确的是( )A、 B、 C、 D、3. 下列因式分解正确的是()A、 B、 C、 D、4. 如图,P为△ABC内一点,连接AP、BP、CP并延长分别交边BC、AC、AB于点D、E、F,则把△ABC分成六个小三角形,其中四个小三角形面积已在图上标明,则△ABC的面积为( )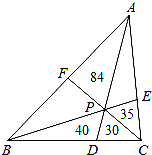 A、300 B、315 C、279 D、3425. 如图,下面推理过程正确的是( )
A、300 B、315 C、279 D、3425. 如图,下面推理过程正确的是( ) A、因为∠B=∠BCD,所以AB∥CD B、因为∠1=∠2.所以AB∥CD C、因为∠BAD+∠B=180°,所以AD∥BC D、因为∠1=∠B,所以AD∥BC6. 已知 , , , 则a,b,c的大小关系是( )A、 B、 C、 D、7. 如图所示、有三种卡片,其中边长为a的正方形卡片有1张,长为a,宽为b的矩形卡片有4张,边长为b的正方形卡片有4张,用这9张卡片刚好供成一个大正方形,则这个大正方形的边长为( )
A、因为∠B=∠BCD,所以AB∥CD B、因为∠1=∠2.所以AB∥CD C、因为∠BAD+∠B=180°,所以AD∥BC D、因为∠1=∠B,所以AD∥BC6. 已知 , , , 则a,b,c的大小关系是( )A、 B、 C、 D、7. 如图所示、有三种卡片,其中边长为a的正方形卡片有1张,长为a,宽为b的矩形卡片有4张,边长为b的正方形卡片有4张,用这9张卡片刚好供成一个大正方形,则这个大正方形的边长为( ) A、a+2b B、2a+2b C、2a+b D、a+b8. 如图, , , , 分别是 , 的平分线,于 . 下列结论:①;②;③;④平分;⑤ . 其中正确结论的个数是( )
A、a+2b B、2a+2b C、2a+b D、a+b8. 如图, , , , 分别是 , 的平分线,于 . 下列结论:①;②;③;④平分;⑤ . 其中正确结论的个数是( )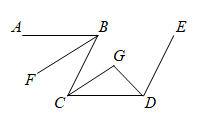 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空3分,共30分)
-
9. 如图,AB∥EF,BC∥DE,则∠E+∠B的度数为.
 10. 如图,已知∠1=∠2,∠B=30°,则∠3=°.
10. 如图,已知∠1=∠2,∠B=30°,则∠3=°. 11. 中国抗疫新型冠状病毒2019−nCoV取得了巨大成就,堪称奇迹,为世界各国防控疫情提供了重要的借鉴和支持,让中国人倍感自豪,该病毒直径在0.00008毫米到0.00012毫米之间,将0.00012用科学记数法表示为.12. 计算的值是 .13. 若 , , 则 .14. 若与的乘积中不含x的一次项,则实数n的值为 .15. 已知某三角形的两条边长分别为4和9,则其第3三边的长可能是 . (写出一个即可)16. 已知一个三角形的面积等于8x3y2﹣4x2y3 , 一条边长等于8x2y2 , 则这条边上的高等于 .
11. 中国抗疫新型冠状病毒2019−nCoV取得了巨大成就,堪称奇迹,为世界各国防控疫情提供了重要的借鉴和支持,让中国人倍感自豪,该病毒直径在0.00008毫米到0.00012毫米之间,将0.00012用科学记数法表示为.12. 计算的值是 .13. 若 , , 则 .14. 若与的乘积中不含x的一次项,则实数n的值为 .15. 已知某三角形的两条边长分别为4和9,则其第3三边的长可能是 . (写出一个即可)16. 已知一个三角形的面积等于8x3y2﹣4x2y3 , 一条边长等于8x2y2 , 则这条边上的高等于 .三、计算题(共24分)
-
17. 计算:(1)、(2)、18. 计算(1)、x5•(-2x)3+x9÷x2•x-(3x4)2(2)、(2a-3b)2-4a(a-2b)(3)、(3x-y)2(3x+y)2(4)、(2a-b+5)(2a+b-5)
四、作图题(共8分)
-
19. 如图,在边长为1个单位的正方形网格中,△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用网格点和无刻度的直尺画图并解答相关的问题(保留画图痕迹):

( 1 )在给定方格纸中画出平移后的△A'B'C';
( 2 )画出AB边上的中线CD;
( 3 )画出BC边上的高线AE;
( 4 )△A'B'C'的面积为____ ;
( 5 )在图中能使S△PAC=S△ABC的格点P的个数有 个(点P异于点B).五、综合题(共7题,共62分)
-
20. 如图,在△ABC中,∠B=36°,∠C=76°,AD是△ABC的角平分线,BE是△ABD中AD边上的高,求∠ABE的度数.
 21. 有这样一道题:计算(2x﹣3)(3x+1)﹣6x(x+3)+25x+15的值,其中x=2018.小刚把x=2018错抄成x=2081,但他的计算结果也是正确的,请通过计算说明原因.22. 已知 , , .(1)、求的值;(2)、求的值.23. 阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.
21. 有这样一道题:计算(2x﹣3)(3x+1)﹣6x(x+3)+25x+15的值,其中x=2018.小刚把x=2018错抄成x=2081,但他的计算结果也是正确的,请通过计算说明原因.22. 已知 , , .(1)、求的值;(2)、求的值.23. 阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.解:∵m2﹣2mn+2n2﹣8n+16=0,
∴(m2﹣2mn+n2)+(n2﹣8n+16)=0
(m﹣n)2+(n﹣4)2=0,
∴(m﹣n)2=0且(n﹣4)2=0,
∴ m=n=4.
根据你的观察,探究下面的问题:
(1)、a2﹣2a+1+b2=0,则a= , b=;(2)、已知x2+2y2﹣2xy+4y+4=0,求xy的值;(3)、已知△ABC的三边长a、b、c都是正整数,且满足2a2+b2﹣4a﹣10b+27=0,求△ABC的周长.24. 如图,是的角平分线, , 交于点E. (1)、若 , , 求的度数;(2)、若 , , 求的度数.25. 将图1中的长方形纸片剪成1号、2号、3号、4号四个正方形和5号长方形,1号正方形的边长为x,2号正方形的边长为y.
(1)、若 , , 求的度数;(2)、若 , , 求的度数.25. 将图1中的长方形纸片剪成1号、2号、3号、4号四个正方形和5号长方形,1号正方形的边长为x,2号正方形的边长为y.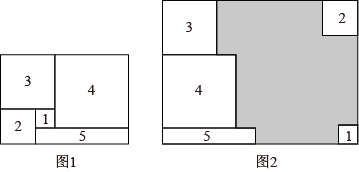 (1)、求5号长方形的面积(用含x,y的代数式表示);(2)、若图1中长方形的周长为24.
(1)、求5号长方形的面积(用含x,y的代数式表示);(2)、若图1中长方形的周长为24.①若2号正方形与1号正方形的面积差为3,求5号长方形的面积;
②将图1中的1号、2号、3号、4号四个正方形和5号长方形按图2的方式放入周长为40的长方形中,则没有覆盖的阴影部分的周长为 ▲ .
26. 我们知道:光线反射时,反射光线、入射光线和法线在同一平面内,反射光线、入射光线分别在法线两侧,反射角等于入射角.如图1,EF为一镜面,AO为入射光线,入射点为点O,ON为法线(过入射点O且垂直于镜面EF的直线),OB为反射光线,此时反射角∠BON等于入射角∠AON.
 (1)、如图1,若∠AOE=65°,则∠BOF=°;若∠AOB=80°,则∠BOF= °;(2)、两平面镜OP、OQ相交于点O,一束光线从点A出发,经过平面镜两次反射后,恰好经过点B.
(1)、如图1,若∠AOE=65°,则∠BOF=°;若∠AOB=80°,则∠BOF= °;(2)、两平面镜OP、OQ相交于点O,一束光线从点A出发,经过平面镜两次反射后,恰好经过点B.①如图2,当∠POQ为多少度时,光线?请说明理由.
②如图3,若两条光线AM、NB相交于点E,请探究∠POQ与∠MEN之间满足的等量关系,并说明理由.
③如图4,若两条光线AM、NB所在的直线相交于点E,∠POQ与∠MEN之间满足的等量关系是 ▲ (直接写出结果)
-