2023年中考数学复习考点一遍过——概率

试卷更新日期：2023-04-17 类型：一轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 抛一枚均匀的骰子，下列事件中，发生可能性最大的是（）

A、点数是奇数 B、点数是3的倍数 C、点数大于5 D、点数小于5

查看试题解析
2. 下列成语所描述的事件属于不可能事件的是（）

A、守株待兔 B、水中捞月 C、水滴石穿 D、百发百中

查看试题解析
3. 下列说法正确的是（）

A、若你在上一个路口遇到绿灯，则在下一路口必遇到红灯 B、某篮球运动员2次罚球，投中一个，则可断定他罚球命中的概率一定为50% C、“明天我市会下雨”是随机事件 D、若某种彩票中奖的概率是1%，则买100张该种彩票一定会中奖

查看试题解析
4. 下列事件是必然事件的是（）

A、足球运动员在罚球区射门一次，射中 B、从煮熟的鸡蛋里孵出小鸡，神奇 C、将实心铅球投入水中，下沉 D、雨后见彩虹，幸运

查看试题解析
5. 10件产品中有5件次品，从中任意抽取1件，恰好抽到次品的概率是（　　）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{5}$

查看试题解析
6. 在一个不透明的盒子中装有n个除颜色外完全相同的球，其中有4个红球.若每次将球充分搅匀后，任意摸出1个球记下颜色再放回盒子，通过大量重复试验后，发现摸到红球的频率稳定在 $20 %$ 左右，则n的值大约为（）

A、16 B、18 C、20 D、24

查看试题解析
7. 利用六张编号为1，2，3，4，5，6的扑克牌进行频率估计概率的试验中，同学小张统计了某一结果出现的频率，绘出的统计图如图所示，则符合这一结果的试验可能是（）

A、抽中的扑克牌编号是3的概率 B、抽中的扑克牌编号是3的倍数的概率 C、抽中的扑克牌编号大于3的概率 D、抽中的扑克牌编号是偶数的概率

查看试题解析
8. 在六张卡片上分别写有5， $- \frac{22}{7}$ ， 3.1415， $π$ ， 0， $\sqrt{2}$ 六个数，从中随机抽取一张，卡片上的数为无理数的概率是（）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{6}$

查看试题解析
9. 如图，一个游戏转盘中，红、黄、蓝三个扇形的圆心角度数分别为 $60 °$ ， $90 °$ ， $210 °$ .让转盘自由转动，转盘停止后指针（指针指向分隔线，则重新转动转盘）落在红色区域的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{6}$ D、 $\frac{7}{12}$

查看试题解析
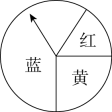10. 在一个暗箱里放有 $m$ 个除颜色外完全相同的球，这 $m$ 个球中红球只有4个，每次将球充分摇匀后，随机从中摸出一球，记下颜色后放回，通过大量的重复试验后发现，摸到红球的频率为0.4，由此可以推算出 $m$ 约为（）

A、7 B、3 C、10 D、6

查看试题解析

二、填空题（每空3分，共15分）

11. 甲、乙、丙三位同学做传球游戏：第一次由甲将球随机传给乙、丙中的某一人，从第二次起，每一次都由持球者将球再随机传给其他两人中的某一人，则第二次传球后球回到甲手里的概率是.

查看试题解析
12. 周末小张和小王去同一个公园跑步，这个公园有 $A$ ， $B$ ， $C$ 三个入口，则他们从同一个入口进入公园的概率是.

查看试题解析
13. 如图，在水平地面上的甲、乙两个区域分别由若干个大小完全相同的正三角形瓷砖组成，琪琪在甲、乙两个区域内分别随意抛一个小球，P（甲）表示小球停留在甲区域中灰色部分的概率，P（乙）表示小球停留在乙区域中灰色部分的概率，则P（甲）P（乙）．（选镇“＞”“＜”或“＝”）

查看试题解析
14. 淘宝某商户为了解新商品主图是否吸引人，对该商品的点击量和展现量进行了监测，得到商品点击率如下表所示：（注： $点击率 = \frac{点击量}{展现量} \times 100 %$ ）
展现量
50
100
1000
5000
10000
50000
100000
点击量
4
7
78
385
760
3800
7600
点击率
$8.0 %$
$7.0 %$
$7.8 %$
$7.7 %$
$7.6 %$
$7.6 %$
$7.6 %$
根据上表，估计该商品展现量为30000时，点击率约为.

查看试题解析
15. 已知不透明的袋中装有红色、黄色、蓝色的乒乓球共120个，某学习小组做“用频率估计概率”的摸球试验（从中随机换出一个球，记下颜色后放回，统计了“摸出球为红色”出现的频率，绘制了如图的折线统计图，那么估计袋中红色球的数目为.（填整十数）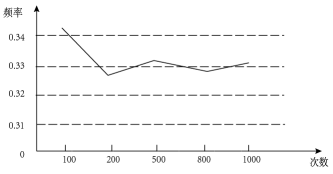

查看试题解析

三、解答题（共8题，共75分）

16. 一个不透明的袋子中装有三个大小、质地都相同的小球，球面上分别标有数字 $1 、 - 2 、 3$ ，搅匀后先从中任意摸出一个小球（不放回），记下数字作为点A的横坐标，再从余下的小球中任意摸出一个小球，记下数字作为A点的纵坐标．

(1)、“A点坐标为 $(0 ， 0)$ ”的事件是事件（填“随机”或“不可能”或“必然”）；

(2)、用列表法或画树状图法列出所有可能出现的结果，并求点A落在第四象限的概率．

查看试题解析
17.

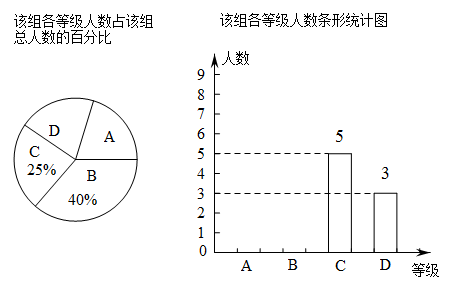(1)、求D等级所对扇形的圆心角，并将条形统计图补充完整；

(2)、该组达到A等级的同学中只有1位男同学，杨老师打算从该组达到A等级的同学中随机选出2位同学在全班介绍经验，请用列表法或画树状图的方法，求出所选两位同学恰好是1位男同学和1位女同学的概率．

查看试题解析
18. 如图，甲、乙两人在玩转盘游戏时，准备了两个可以自由转动的转盘A，B，每个转盘被分成面积相等的几个扇形，并在每一个扇形内标上数字．游戏规则：同时转动两个转盘，当转盘停止后，指针所指区域的数字之和为1时，甲获胜；数字之和为2时，乙获胜．如果指针恰好指在分割线上，那么重转一次，直到指针指向某一区域为止．

(1)、用画树状图或列表法求乙获胜的概率；

(2)、这个游戏规则对甲、乙双方公平吗？对谁有利？请判断并说明理由．

查看试题解析
19. 为了贯彻“减负增效”精神，某校掌握2022～2023学年度九年级600名学生每天的自主学习情况，某校学生会随机抽查了2022～2023学年度九年级的部分学生，并调查他们每天自主学习的时间.根据调查结果，制作了两幅不完整的统计图（图1，图2），请根据统计图中的信息回答下列问题：

(1)、本次调查的学生人数有人；

(2)、图2中α是 ▲ 度，并将图1补充完整；

(3)、请估算该校2022～2023学年度九年级学生自主学习时间不少于1.5小时的有人；

(4)、老师想从学习效果较好的4位同学（分别记为A、B、C、D，其中A为小亮）中随机选择两位进行学习经验交流，用列表法或画树状图的方法求出选中小亮的概率.

查看试题解析
20. 学校某数学调查小组通过随机调查了某社交App的6000名用户（男性4000人，女性2000人），从中随机抽取了60人（其中女性20人），统计他们在日常消费时是否使用手机支付的情况，定义：使用手机支付的为“手机支付族”，其他的为“非手机支付族”．根据抽样数据，绘制如下统计表．

手机支付族
非手机支付族
合计
男
30
10
40
女
a
8
20
合计
42
b
60

(1)、① $a =$ ▲ ， b ▲ ；
②用样本估计总体，若从该社交App女性用户中随机抽取1位，这位女性用户是“手机支付族”的概率是多少?

(2)、某商场对“手机支付族”和“非手机支付族”有奖酬宾活动：凡购物满100元，均可得到一次抽奖的机会．在一个纸盒里装有2个红球和2个白球，它们除颜色外其他都相同，抽奖者一次从中摸出两个球，根据球的颜色决定赠送相应券值的礼金券．（如下表）
手机支付族：
球
两红
一红一白
两白
礼金券/元
5
10
5
非手机支付族：
球
两红
一红一白
两白
礼金券/元
10
5
10
①用树状图表示某顾客进行一次摸奖的结果的所有情况；
②如果只考虑中奖因素，你将会选择哪种付费方式?请说明理由．

查看试题解析
21. 为落实中小学课后服务工作的要求，某校开设了四门校本课程供学生选择：A（合唱社团）、B（陶艺社团）、C（数独社团）、D（硬笔书法），七年级共有120名学生选择了C课程．为了解选择C课程学生的学习情况，张老师从这120名学生中随机抽取了30名学生进行测试，将他们的成绩（百分制，单位：分）分成六组，绘制成频数分布直方图．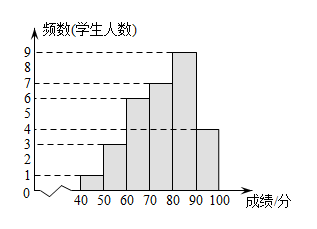

(1)、 $80 ～ 90$ 分这组的数据为：81、89、84、84、84、86、85、88、83，则这组数据的中位数是分、众数是分；

(2)、根据题中信息，可以估算七年级选择C课程的学生成绩在 $70 ～ 90$ 分的人数是人；

(3)、七年级每名学生必须选两门不同的课程，小明和小华在选课程的过程中，第一门都选了课程C．他俩决定随机选择第二门课程，请用列表法或树状图的方法求他俩同时选到课程A或课程B的概率．

查看试题解析

22. 在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个，小明做摸球实验，他将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是实验中的一组统计数据：

摸球的次数n	100	200	300	500	800	1000	3000
摸到白球的次数m	70	128	171	302	481	599	903
摸到白球的频率 $\frac{m}{n}$	0.75	0.64	0.57	0.604	0.601	0.599	0.602

(1)、请估计：当n很大时，摸到白球的概率约为.（精确到0.1）

(2)、估算盒子里有白球个.

(3)、若向盒子里再放入x个除颜色以外其它完全相同的球，这x个球中白球只有1个，每次将球搅拌均匀后，任意摸出一个球记下颜色再放回，通过大量重复摸球试验后发现，摸到白球的频率稳定在50%，那么可以推测出x最有可能是.

查看试题解析

23. 2022年3月23日15：40，“天宫课堂”第二课开讲，本次太空授课活动同样采取天地对话方式进行，在约45分钟的授课中，神舟十三号飞行乘组生动演示了微重力环境下太空“冰雪”实验、液桥演示实验、水油分离实验、太空抛物实验．某校组织全体学生观看了本次授课活动，并让同学们选出自己最感兴趣的实验．学校教务处随机抽取了部分学生对授课活动最感兴趣的实验进行了问卷调查，具体问卷如下：
将调查结果绘制成如下所示的条形统计图和扇形统计图（均不完整）
请根据统计图中提供的信息，解答下列问题：

(1)、参与本次问卷调查的总人数为人；在扇形统计图中，“太空抛物实验”的圆心角是度．

(2)、请将条形统计图补充完整．

(3)、若该校有3600名学生，请你估计选择太空“冰雪”实验的有多少人．

(4)、为弘扬科学精神，传播航天知识、感悟榜样精神与力量，学校教务处决定开展
“飞天梦永不失重，科学梦张力无限”的主题活动，包含了以下四个内容：A．书写观后感；B．演示科学实验；C．绘制手抄报；D．开展主题班会．王老师在四张完全相同的卡片上分别写了A，B，C，D，然后背面朝上放置，搅匀后要求先由七年级派一名代表从中随机抽取一张，记下标号后放回，再由八年级派一名代表从中随机抽取一张，请用列表或画树状图的方法，求两个年级代表抽到的主题卡片中有演示科学实验（B）的概率．

查看试题解析

展现量	50	100	1000	5000	10000	50000	100000
点击量	4	7	78	385	760	3800	7600
点击率	$8.0 %$	$7.0 %$	$7.8 %$	$7.7 %$	$7.6 %$	$7.6 %$	$7.6 %$

	手机支付族	非手机支付族	合计
男	30	10	40
女	a	8	20
合计	42	b	60

球	两红	一红一白	两白
礼金券/元	5	10	5

球	两红	一红一白	两白
礼金券/元	10	5	10