鲁教版（五四制）2022-2023学年度第二学期六年级数学用尺规作角期中复习

试卷更新日期：2023-04-17 类型：复习试卷

进入出卷网下载

一、单选题

1. 一把三角尺和一把直尺如图摆放，已知∠BAC是直角，且∠BAC的顶点A在直尺的边DE上，那么在下列结论中，不一定成立的（）

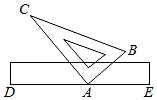A、∠BAE与∠CAD互余 B、∠BAD＝∠CAE C、∠CAE＞∠BAE D、∠BAE＝180°﹣∠CAD﹣∠CAB

查看试题解析
2. 如图，已知∠AOB与∠EO′F，分别以O，O′为圆心，以同样长为半径画弧，分别交OA，OB于点A′，B′，交O′E，O′F于点E′，F′，以B′为圆心，以E′F′长为半径画弧，交弧A′B′于点A″．下列结论错误的是（）

A、∠AOB＝2∠EO′F B、∠AOB＞∠EO′F C、∠A″OB＝∠EO′F D、∠AOA″＝∠AOB﹣∠EO′F

查看试题解析
3. 如图所示， $∠ A O B = 90 °$ ， $∠ B O C = 40 °$ ， OD平分 $∠ A O C$ ，则 $∠ B O D$ 的度数是（）

A、 $25 °$ B、 $30 °$ C、 $40 °$ D、 $60 °$

查看试题解析
4. 若∠1=50°5′，∠2=50.5°，则∠1与∠2的大小关系是（）

A、∠1=∠2 B、∠2>∠1 C、∠1>∠2 D、无法确定

查看试题解析
5. 若 $∠ A = 99.6 °$ ， $∠ B = 99 ° 3 5^{'} 5 4^{″}$ ，则 $∠ A$ 与 $∠ B$ 的大小关系是（）

A、 $∠ A > ∠ B$ B、 $∠ A = ∠ B$ C、 $∠ A < ∠ B$ D、无法判断

查看试题解析
6. 如图，一副三角板（直角顶点重合）摆放在桌面上，若 $∠ A O D = 160 °$ ，则 $∠ B O C$ 等于（）

A、 $20 °$ B、 $30 °$ C、 $40 °$ D、 $50 °$

查看试题解析
7. 如图，∠AOC与∠BOC互为余角，OD平分∠BOC，∠EOC＝2∠AOE.若∠COD＝18°，则∠AOE的大小是（）

A、12° B、15° C、18° D、24°

查看试题解析
8. 下列说法正确的有（）个
①两点确定一条直线；②两点之间，直线最短；③角的两边越长，角就越大；④若线段 $A B = B C$ ，则点B是线段 $A C$ 的中点.

A、4个 B、3个 C、2个 D、1个

查看试题解析
9. 借助一副三角尺的拼摆，你能画出（）度的角.

A、65 B、70 C、75 D、85

查看试题解析
10. 如图所示的网格是正方形网格，则∠AOB与∠MPN的关系是（）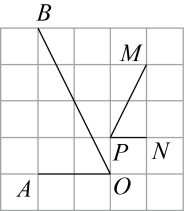

A、∠AOB＞∠MPN B、∠AOB＜∠MPN C、∠AOB＝∠MPN D、∠AOB＝2∠MPN

查看试题解析

二、填空题

11. 如图所示的网格是正方形网格，点 A，B，C，D，O 是网格线交点，那么 $∠ A O B$ $∠ C O D$

查看试题解析
12. 如图所示， $O$ 是直线 $A C$ 上一点， $O B$ 是一条射线， $O D$ 平分 $∠ A O B$ ， $O E$ 在 $∠ B O C$ 内， $∠ B O E = \frac{1}{3} ∠ E O C$ ， $∠ D O E = 60 °$ ，则 $∠ E O C$ 的度数是．

查看试题解析
13. 如图，C为直线 $A B$ 上一点， $∠ D C E$ 为直角， $C F$ 平分 $∠ A C D$ ， $C H$ 平分 $∠ B C D$ ， $C G$ 平分 $∠ B C E$ ，则 $∠ A C F - ∠ B C G =$ .

查看试题解析
14. 比较大小： $60 ° 2 5^{'}$ $60.25 °$ （填“ $>$ ”，“ $<$ ”或“ $=$ ”）．

查看试题解析
15. 用10倍放大镜看30°的角，你观察到的角是.

查看试题解析

三、解答题

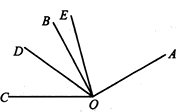
16. 如图，OD是∠BOC的平分线，OE是∠AOC的平分线，∠AOB︰∠BOC=3︰2，若∠BOE=13°，求∠DOE的度数.

查看试题解析
17. 如图，直线AB、CD相交于点O，OE平分∠AOD，OF⊥CD，∠AOE=70°，求∠BOF的度数.

查看试题解析
18. 尺规作图：已知线段a和 $∠ α$ ．作一个 $△ A B C$ ，使 $B C = a$ ， $A C = 2 a$ ， $∠ B C A = ∠ α$ ．
要求：不写作法，保留作图痕迹．

查看试题解析

四、综合题

19. 如图， $A B$ 是直线， $O D ， O E$ 分别是 $∠ A O C ， ∠ B O C$ 的平分线.

(1)、 $∠ B O C = 72 ° 2 0^{'}$ ，求 $∠ 1 ， ∠ 2 ， ∠ D O E$ 的度数.

(2)、若 $∠ B O C = α$ ，求 $∠ D O E$ .

查看试题解析
20. 如图，点A，O，B在同一条直线上， $∠ A O C = ∠ B O D$ ， $O M$ ， $O N$ 分别是 $∠ A O C$ ， $∠ B O D$ 的平分线.

(1)、若 $∠ C O D = 80 °$ ，求 $∠ M O N$ 的度数；

(2)、比较 $∠ D O M$ 和 $∠ C O N$ 的大小，并说明理由.

查看试题解析
21. 如图，已知直线 $A B$ 与 $C D$ 相交于点O， $O E$ 平分 $∠ A O D$ .

(1)、若 $∠ A O C = 50 °$ ，求 $∠ B O E$ 的度数.

(2)、直接写出图中与 $∠ B O E$ 相等的角：.

查看试题解析
22. 如图，直线AB、CD相交于点O，OA平分∠EOC.

(1)、若∠EOC=70°，求∠BOD的度数；

(2)、若∠EOC= $\frac{2}{3}$ ∠EOD，求∠BOD的度数.

查看试题解析
23. 已知，O是直线 $A B$ 上的一点， $∠ C O D$ 是直角， $O E$ 平分 $∠ B O C$ .

(1)、如图1，若 $∠ A O C = 36 °$ ，求 $∠ D O E$ 的度数；

(2)、将图1中的 $∠ D O C$ 绕顶点O顺时针旋转至图2的位置.
①探究 $∠ A O D$ （小于平角）和 $∠ D O E$ 的度数之间的关系，写出你的结论，并说明理由.

②在 $∠ A O C$ （小于平角）的内部有一条射线OF，满足： $3 ∠ C O F + 2 ∠ B O E = \frac{1}{2} (∠ A O D + 4 ∠ A O F)$ ，试确定 $∠ A O F$ 与 $∠ B O E$ 的之间的数量关系，并说明理由.

查看试题解析

鲁教版（五四制）2022-2023学年度第二学期六年级数学 用尺规作角 期中复习

一、单选题

二、填空题

三、解答题

四、综合题

鲁教版（五四制）2022-2023学年度第二学期六年级数学用尺规作角期中复习