鲁教版（五四制）2022-2023学年度第二学期六年级数学 平行线的性质 期中复习
试卷更新日期：2023-04-17 类型：复习试卷
一、单选题
-
1. 如图，已知直线AB∥CD．DA⊥CE于点A．若∠D＝36°20′，则∠EAB的度数是（ ）
A、63°40′ B、53°40′ C、44°40′ D、36°20′2. 在同一平面内，若∠A与∠B的两边分别平行，且∠A比∠B的3倍少40°，则∠A的度数为（ ）A、20° B、55° C、20°或125° D、20°或55°3. 如图直线l1∥l2 ， AB⊥CD，∠1＝34°，那么∠2的度数是（ ）
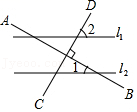A、34° B、56° C、46° D、44°4. 如图，A，B，C，D，E分别在的两条边上，若 ， ， ， ， ， 则下列结论中错误的是（ ）
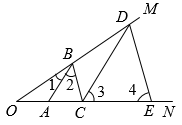A、 B、 C、 D、5. 一副直角三角板如图放置，点C在的延长线上， ， ， ， ， 则为（ ）
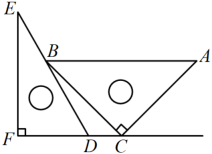A、 B、 C、 D、6. 直线、、中， ， ， 则直线与直线的关系是（ ）.A、相交 B、平行 C、垂直 D、不能确定7. 下列图形中，根据 ， 能得到的是（ ）A、
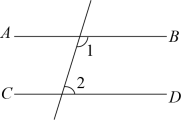B、
C、
D、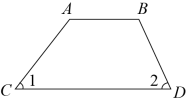
8. 如图，已知直线a∥b，直线a、b被直线c所截，若∠1=58°，则∠2的度数为（ ）
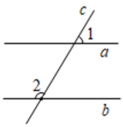A、132° B、122° C、58° D、22°9. 如图，四边形ABCD是梯形， ， 与 的角平分线交于点E， 与 的角平分线交于点F，则 与 的大小关系为（ ）
A、 B、 C、 D、无法确定10. 如图，已知直线AD∥BC，BE平分∠ABC交直线DA于点E，若∠DAB＝54°，则∠E等于（ ）
A、25° B、27° C、29° D、45°二、填空题
-
11. 如图，在四边形中， ， ， 则度.
12. 如图，已知DEBC，BE平分∠ABC，若∠1=70°，则∠AEB的度数为.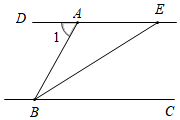
13. 有一条长方形纸带，按如图所示沿折叠，若 ， 则纸带重叠部分中°.
14. 一副直角三角板如图放置，点C在的延长线上， ， ， 则的度数为 ．
15. 将含30°角的三角板如图摆放，AB CD，若 ＝20°，则 的度数是.
三、解答题
-
16. 如图， ， ， 直线与平行吗？直线与平行吗？说明理由.（请在下面的解答过程的空格内填空或在括号内填写理由）
解：直线与平行，直线与平行，理由如下：
∵ ， （已知）
∴ ▲ ， （ ）
∴ ， （ ）
又∵ ， （已知）
∴ ▲ ， （等量代换）
∴ ▲ ， （ ）.
17. 如图，AB∥CD，CB平分∠ACD，∠ACD＝140°，∠CBF＝20°，∠EFB＝130°．求∠CEF的度数．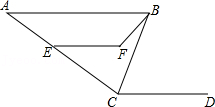
18. 如图，AB∥CD，∠FGB＝154°，FG平分∠EFD，求∠AEF的度数．
四、综合题
-
19. 如图，∠AFD＝∠1，AC∥DE．
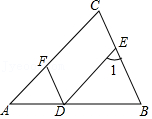(1)、试说明：DF∥BC；(2)、若∠1＝68°，DF平分∠ADE，求∠B的度数．20. 如图，已知∠EAF＝∠NCM＝∠MCB＝46°．
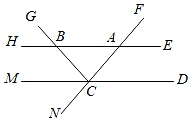(1)、请说明AB∥CD．（把说明理由的过程补充完整，括号里面填写结论得出的依据）理由：∵∠ACD＝∠＝46°（），
又∵∠EAF＝46°，
∴∠EAF＝∠ACD，
∴AB∥CD（）．
(2)、求∠ABG的度数．21. 如图，直线MN分别与直线AC、DG交于点B、F，且∠1=∠2．∠ABF的角平分线BE交直线DG于点E．∠BFG的角平分线FC交直线AC于点C．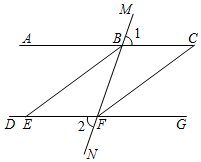
(1)、求证：BE∥CF：(2)、若∠C=35°．求∠BED的度数。22. 如图，在△ABC中，点D在边BC上，点G在边AB上，点E、F在边AC上，∠AGF=∠ABC =70° ，∠1+∠2=180° .
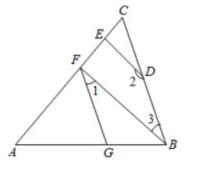(1)、试判断BF与DE的位置关系，并说明理由：(2)、若DE⊥AC，∠2=150°，求∠AFG的度数.23. 已知：如图1，直线AB、CD被直线MN所截，且AB∥CD．点E在直线AB、CD之间的线段MN上，P、Q分别在直线AB、CD上，连接PE、EQ．
(1)、小明探究发现：∠PEQ＝∠APE+∠CQE，请你帮小明说明理由；(2)、如图2，已知∠FPB＝ ∠EPB，∠FQD＝ ∠EQD，若∠PEQ＝80°，请你利用小明发现的结论求∠PFQ的度数；(3)、如图3，若∠FPB＝ ∠EPB，∠FQD＝ ∠EQD，请你直接写出∠PEQ和∠PFQ之间的数量关系．