鲁教版(五四制)2022-2023学年度第二学期六年级数学 探索直线平行的条件 期中复习
试卷更新日期:2023-04-17 类型:复习试卷
一、单选题
-
1. 如果两条平行线被第三条直线所截,那么其中一组同位角的角平分线( )A、垂直 B、相交 C、平行 D、不能确定2. 在如图所示的四种沿AB进行折叠的方法中,不一定能判断纸带两条边a,b互相平行的是( )
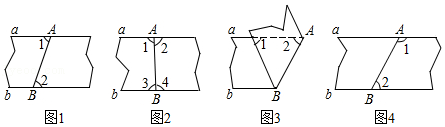 A、如图1,展开后测得∠1=∠2 B、如图3,测得∠1=∠2 C、如图2,展开后测得∠1=∠2且∠3=∠4 D、在图4,展开后测得∠1+∠2=180°3. 下列四个选项中,∠1与∠2是同位角的是( )A、
A、如图1,展开后测得∠1=∠2 B、如图3,测得∠1=∠2 C、如图2,展开后测得∠1=∠2且∠3=∠4 D、在图4,展开后测得∠1+∠2=180°3. 下列四个选项中,∠1与∠2是同位角的是( )A、 B、
B、 C、
C、 D、
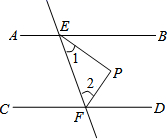
D、 4. 如图,下列能判定∥的条件有几个( )(1)、 (2)(3) (4).
4. 如图,下列能判定∥的条件有几个( )(1)、 (2)(3) (4).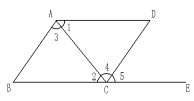 A、4 B、3 C、2 D、15. 如图,下列判断中正确的是( )
A、4 B、3 C、2 D、15. 如图,下列判断中正确的是( )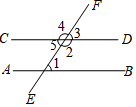 A、如果 , 那么 B、如果 , 那么 C、如果 , 那么 D、如果 , 那么6. 如图所示,给出下列条件:①∠1=∠B;②∠EFD+∠B=180°;③∠B=∠D;④∠E=∠B;⑤∠BFD=∠B.其中,一定能判断AB∥CD的条件的个数为( )
A、如果 , 那么 B、如果 , 那么 C、如果 , 那么 D、如果 , 那么6. 如图所示,给出下列条件:①∠1=∠B;②∠EFD+∠B=180°;③∠B=∠D;④∠E=∠B;⑤∠BFD=∠B.其中,一定能判断AB∥CD的条件的个数为( ) A、2个 B、3个 C、4个 D、5个7. 如图所示,不能推出AD∥BC的是( )
A、2个 B、3个 C、4个 D、5个7. 如图所示,不能推出AD∥BC的是( ) A、∠DAB+∠ABC=180° B、∠2=∠4 C、∠1=∠3 D、∠CBE=∠DAE8. 如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠7+∠4﹣∠1=180°,⑤∠7=∠2+∠3,⑥∠2=∠3中能判断直线a∥b的有( )
A、∠DAB+∠ABC=180° B、∠2=∠4 C、∠1=∠3 D、∠CBE=∠DAE8. 如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠7+∠4﹣∠1=180°,⑤∠7=∠2+∠3,⑥∠2=∠3中能判断直线a∥b的有( )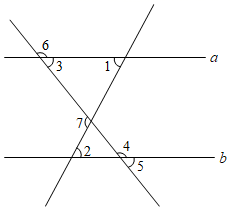 A、3个 B、4个 C、5个 D、6个9. 为了检验一条纸带的两条边线是否平行,小明沿折叠后,如图,测量得到:①;②;③;④ . 其中能够判定两条边线、互相平行的个数是( )
A、3个 B、4个 C、5个 D、6个9. 为了检验一条纸带的两条边线是否平行,小明沿折叠后,如图,测量得到:①;②;③;④ . 其中能够判定两条边线、互相平行的个数是( ) A、1 B、2 C、3 D、410. 如图,直线b、c被直线a所截,则与是( )
A、1 B、2 C、3 D、410. 如图,直线b、c被直线a所截,则与是( ) A、对顶角 B、同位角 C、内错角 D、同旁内角
A、对顶角 B、同位角 C、内错角 D、同旁内角二、填空题
-
11. 如图,不添加辅助线,请写出一个能判定ADBC的条件 .
 12. 如图,若 , 被 所截,则 与是内错角.
12. 如图,若 , 被 所截,则 与是内错角. 13. 如图,已知AB∥CD, =
13. 如图,已知AB∥CD, = 14. 如图, ,点M为CD上一点,MF平分∠CME.若∠1=57°,则∠EMD的大小为度.
14. 如图, ,点M为CD上一点,MF平分∠CME.若∠1=57°,则∠EMD的大小为度. 15. 如图,给出下列条件:① ;② ;③ ;④ ;⑤ .其中,一定能判定 ∥ 的条件有(填写所有正确的序号).
15. 如图,给出下列条件:① ;② ;③ ;④ ;⑤ .其中,一定能判定 ∥ 的条件有(填写所有正确的序号).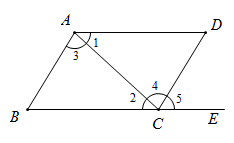
三、解答题
-
16. 如图,如果 , , 试说明与平行.请完善解答过程,并填空(理由或数学式).

解:∵( )
∴( )(内错角相等,两直线平行.)
∴( )
∵(已知)
∴( )( )
∴( )
17. 如图,A、B是直线MN上的两个点,且不重合,分别过点A、B作直线MN的垂线AC、BD,点C、D在直线MN的同侧.若 , , 则AC与BD平行吗?AE与BF平行吗?完成下面的解答过程,并填空(理由或数学式).
解:∵ , ( )
∴( )
∵ ,
∴( )
∴ ,
同理可得 ,
∵ , ,
∴( )( )
∴( )=∠2.
∴( ).
18. 如图,已知:∠1=∠2,求直线a,b的关系.
四、综合题
-
19.(1)、如图,已知 , , 求证: .
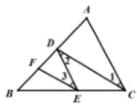
证明:∵ ,
∴∠ ▲ =∠ ▲ (两直线平行, ▲ )
又∵ ,
∴∠ ▲ =∠ ▲ ,
∴ ▲ ▲ . ( ▲ , 两直线平行)
(2)、如图,已知 , , 求证: .20. 如图, 和 的边BC、DF在同一直线上(D点在C点的左边),已知 , , . (1)、求证: .(2)、求证: .
(1)、求证: .(2)、求证: .