鲁教版（五四制）2022-2023学年度第二学期六年级数学平方差公式期中复习

试卷更新日期：2023-04-17 类型：复习试卷

进入出卷网下载

一、单选题

1. 如图所示，将四张全等的长方形硬纸片围成一个正方形，根据图形阴影部分面积的关系，可以直观地得到一个关于a、b的恒等式为（）

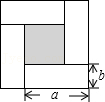A、a²﹣b²＝（a+b）（a﹣b） B、（a+b）²＝a²+2ab+b² C、（a﹣b）²＝（a+b）²﹣4ab D、a²+ab＝a（a+b）

查看试题解析
2. 若代数式M•（3x﹣y²）＝y⁴﹣9x² ，那么代数式M为（）

A、﹣3x﹣y² B、﹣3x+y² C、3x+y² D、3x﹣y²

查看试题解析
3. 下列多项式乘法中，不能用平方差公式计算的是（）。

A、（﹣x﹣y）（x﹣y） B、（﹣x+y）（x﹣y） C、（﹣x﹣y）（﹣x+y） D、（x+y）（﹣x+y）

查看试题解析
4. 如果用平方差公式计算 $(x - y + 5) (x + y + 5)$ ，则可将原式变形为（）

A、 $[(x - y) + 5] [(x + y) + 5]$ B、 $[(x - y) + 5] [(x - y) - 5]$ C、 $[(x + 5) - y] [(x + 5) + y]$ D、 $[x - (y + 5)] [x + (y + 5)]$

查看试题解析
5. 如图，从边长为a的大正方形中去掉一个边长为b的小正方形，然后将剩余部分剪后拼成一个长方形，则这个长方形的周长为（）

A、 $2 (a + b)$ B、 $2 a + b$ C、 $4 a$ D、 $2 (a - b)$

查看试题解析
6. 下列多项式乘以多项式中，能用平方差公式计算的是（）

A、 $(- x - y) (- x + y)$ B、 $(x - y) (- x + y)$ C、 $(- x - y) (x + y)$ D、 $(- x - y) (- x - y)$

查看试题解析
7. 已知 $a$ ， $b$ 为实数，下列说法：①若 $a b < 0$ ，且 $a$ ， $b$ 互为相反数，则 $\frac{a}{b} = - 1$ ；②若 $| a - b | + a - b = 0$ ，则 $a - b = 0$ ；③若 $a < b$ ， $a b < 0$ 且 $| a | < | b |$ ，则 $a + b < 0$ ；④若 $a + b < 0$ ， $a b > 0$ ，则 $| - 2 a - 3 b | = 2 a + 3 b$ ；⑤若 $| a | > | b |$ ，则 $(a + b) (a - b) < 0$ ，其中正确个数为 $($ $)$

A、1 B、2 C、3 D、4

查看试题解析
8. （2+1）（2²+1）（2⁴+1）…（2¹⁶+1）的结果为（）

A、2³²-1 B、2³²+1 C、2³² D、2¹⁶

查看试题解析
9. 记 $x = (1 + 2) (1 + 2^{2}) (1 + 2^{4}) (1 + 2^{8}) \dots (1 + 2^{n})$ ，且 $x + 1 = 2^{128}$ ，则 $n =$ （）．

A、128 B、32 C、64 D、16

查看试题解析
10. 如图，在边长为a的正方形中挖掉一个边长为b的小正方形，把余下的部分拼成一个长方形（无重叠部分），通过计算两个图形中阴影部分的面积，可以验证的一个等式是（）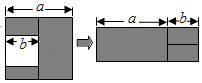

A、a²﹣b²＝（a+b）（a﹣b） B、a（a﹣b）＝a²﹣ab C、（a﹣b）²＝a²﹣2ab+b² D、a（a+b）＝a²+ab

查看试题解析

二、填空题

11. 观察下列各式： $(x - 1) (x + 1) = x^{2} - 1$ ； $(x - 1) (x^{2} - x + 1) = x^{3} - 1$ ； $(x - 1) (x^{3} + x^{2} + x + 1) = x^{4} - 1$ ；……根据前面各式的规律可得到 $(x - 1) (x^{n} + x^{n - 1} + x^{n - 2} + ⋯ + x + 1) =$ ．

查看试题解析
12. 若 $S = (1 - \frac{1}{2^{2}}) \times (1 - \frac{1}{3^{2}}) \times \dots \times (1 - \frac{1}{2021^{2}}) (1 - \frac{1}{2022^{2}})$ ，则 $S$ 的值为．

查看试题解析
13. 根据公式x²﹣y²＝（x+y）（x﹣y）来解题有时能起到简化计算的效果.比如计算50²﹣49＝（50+49）×（50﹣49）＝99×1＝99，根据这种方法计算（ $\frac{9}{11}$ ）²﹣（ $\frac{2}{11}$ ）²结果是

查看试题解析
14. 计算： $99 . 8^{2} - 0 . 2^{2} =$ ．

查看试题解析
15. 若a+b＝﹣3，ab＝1，则（a+1）（b+1）（a﹣1）（b﹣1）＝．

查看试题解析

三、解答题

16. 计算：（a-2b+3c）（a+2b-3c）．

查看试题解析
17. 已知关于 $x$ 的多项式 $4 x^{2} - 5 k x - 9$ 减去 $(\frac{k}{3} x + 3) (\frac{k}{3} x - 3)$ 的差是一个单项式，求 $- k^{2} + 3 k - 1$ 的值．

查看试题解析
18. 先化简，再求值：（2x）²﹣[（3x﹣1）（3x＋1）﹣（x＋3）（x﹣5）﹣（2x﹣3）²]，其中x＝﹣ $\frac{1}{2}$ ．

查看试题解析

四、综合题

19. 计算

(1)、 $(a - 2 b + c) (a + 2 b - c)$ ；

(2)、已知： $x + y = 3$ ， $x y = - 7$ ，求：
① $x^{2} + y^{2}$ ；
② ${(x - y)}^{2}$ .

查看试题解析
20. 已知关于x的多项式A，当A-（x-2）²=x（x+7）时，完成下列各题：

(1)、求多项式A；

(2)、若x²+ $\frac{3}{2}$ x+1=0，求多项式A的值．

查看试题解析
21. 填表并回答问题：
x
1
1
0
2
y
2
3
3
1
（x+y）（x﹣y）
x²﹣y²

(1)、观察并填出表，你有何发现，将你的发现写在横线上：．

(2)、利用你发现的结果计算：2022²﹣2021² ．

查看试题解析
22. 实践与探索
如图1，边长为 $a$ 的大正方形有一个边长为 $b$ 的小正方形，把图1中的阴影部分拼成一个长方形（如图2所示）

(1)、上述操作能验证的等式是____；（请选择正确的一个）

A、 $a^{2} - b^{2} = (a + b) (a - b)$ B、 $a^{2} - 2 a b + b^{2} = {(a - b)}^{2}$ C、 $a^{2} + a b = a (a + b)$

(2)、请应用这个公式完成下列各题：
①已知 $4 a^{2} - b^{2} = 24$ ， $2 a + b = 6$ ，则 $2 a - b =$ ▲ ．
②计算： $10 0^{2} - 9 9^{2} + 9 8^{2} - 9 7^{2} + ⋯ + 4^{2} - 3^{2} + 2^{2} - 1^{2}$

查看试题解析
23. 如图，正方形 $A B C D$ 的边长等于 $a$ ，正方形 $B E F G$ 的边长等于 $b (a > b)$ ，其中，点 $G 、 E$ 分别在 $A B 、 B C$ 上．

(1)、用 $a 、 b$ 的代数式表示图中的阴影部分面积；

(2)、当 $a = 5 ， b = 2$ 时，求图中的阴影部分面积．

查看试题解析

x	1	1	0	2
y	2	3	3	1
（x+y）（x﹣y）
x²﹣y²

鲁教版（五四制）2022-2023学年度第二学期六年级数学 平方差公式 期中复习

一、单选题

二、填空题

三、解答题

四、综合题

鲁教版（五四制）2022-2023学年度第二学期六年级数学平方差公式期中复习