鲁教版（五四制）2022-2023学年度第二学期六年级数学整式的乘法期中复习

试卷更新日期：2023-04-17 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、m+2m＝3m² B、2m³•3m²＝6m⁶ C、（2m）³＝8m³ D、m⁶÷m²＝m³

查看试题解析
2. 下列运算正确的是（）

A、3（a³）²＝6a⁶ B、（a﹣2）（a﹣3）＝a²﹣5a+6 C、x⁸÷x⁴＝x² D、3x³•2x²＝6x⁶

查看试题解析
3. 如图，正方形卡片A类，B类和长方形卡片C类若干张，如果要拼一个长为(a+2b)，宽为(3a+b)的大长方形，则需要C类卡片的张数为（）

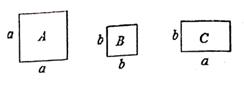A、5张 B、6张 C、7张 D、8张

查看试题解析
4. 若x²+2(m-3)x+1是完全平方式，x+n与x+2的乘积中不含x的一次项，则n^m的值为（）

A、-4 B、16 C、4或16 D、-4或-16

查看试题解析
5. 下列计算正确的是（）

A、(2x+y)(3x-y)=6x²-y² ． B、(-x+2y)²=x²-4xy+4y² ． C、(m+n)³(m+n)²=m⁵+n⁵ D、(2x- $\frac{1}{2}$ y)²=4x²-xy+ $\frac{1}{4}$ y²

查看试题解析
6. 如果计算 $(x + a) (x - 2)$ 的结果是一个二项式，那么a的值是（）

A、1 B、2或0 C、3 D、4

查看试题解析
7. 如果 $(x - 3) (x + 4) = x^{2} + p x + q$ ，那么 $p 、 q$ 的值是（）

A、 $p = 1$ ， $q = 12$ B、 $p = 1$ ， $q = - 12$ C、 $p = - 1$ ， $q = 12$ D、 $p = - 1$ ， $q = - 12$

查看试题解析
8. 下列多项式中，与 $- 3 x + y$ 相乘的结果是 $- 3 x^{2} + 10 x y - 3 y^{2}$ 的多项式是（）

A、 $x + 3 y$ B、 $x - 3 y$ C、 $3 x + y$ D、 $3 x - y$

查看试题解析
9. 如果A、B都是关于x的单项式，且A·B是一个九次单项式，A+B是一个五次多项式，那么A-B的次数（）

A、一定是四次； B、一定是五次； C、一定是九次； D、无法确定.

查看试题解析
10. 下列有四个结论，其中正确的是（）
①若 ${(x - 1)}^{x + 1} = 1$ ，则 $x$ 只能是 $2$ ；②若 $(x - 1) (x^{2} + a x + 1)$ 的运算结果中不含 $x^{2}$ 项，则 $a = 1$ ③若 $a + b = 10$ ， $a b = 2$ ，则 $a - b = 2$ ④若 $4^{x} = a$ ， $8^{y} = b$ ，则 $2^{2 x - 3 y}$ 可表示为 $\frac{a}{b}$

A、①②③④ B、②③④ C、①③④ D、②④

查看试题解析

二、填空题

11. 若 $(x - 1) (x + 6) = x^{2} + m x - 6$ ，则 $m^{2} - 4$ 的结果为.

查看试题解析
12. 若 $(5 x - 3 b) (a x + 1) = 20 x^{2} - 7 x - c$ ，则 ${(a + c)}^{b} =$ ．

查看试题解析
13. 计算： $(3 x - 2) (x + 2) =$ ．

查看试题解析
14. 已知 $(m x + n) (x^{2} - 3 x + 4)$ 展开式中不含 $x^{2}$ 项，且 $x^{3}$ 的系数为2．则 $n^{m}$ 的值为．

查看试题解析
15. 若m，n为常数，等式（x+2）（x-1）=x²+mx+n恒成立，则mⁿ的值为．

查看试题解析

三、解答题

16. 已知二次三项式 $x^{2} - 2 x + 3$ 与多项式 $a x + b$ （a、b为常数）相乘，积中不出现二次项，且一次项系数为 $- 1$ ，求 $a$ 、 $b$ 的值．

查看试题解析
17. 甲、乙两人共同计算一道整式： $(x + a) (2 x + b)$ ．由于甲抄错了 $a$ 的符号，得到的结果是 $2 x^{2} - 7 x + 3$ ，乙漏抄了第二个多项式中 $x$ 的系数，得到的结果是 $x^{2} + 2 x - 3$ ．求 $(a - b) (- 2 a - b)$ 的值．

查看试题解析
18. 小明在进行两个多项式的乘法运算时，不小心把乘 $(x - 2 y)$ 错抄成除以 $(x - 2 y)$ ，结果得到 $3 x$ ，如果小明没有错抄题目，并且计算依然符合题意，那么得到的结果应该是什么？

查看试题解析

四、综合题

19. 如图，用同样规格黑白两色的正方形瓷砖铺设长方形地面．请观察下列图形并解答有关问题：

(1)、在第n个图中，第一横行共块瓷砖，第一竖列共有块瓷砖；（均用含n的代数式表示）

(2)、在铺设第n个图形时，共用多少块瓷砖？

(3)、若黑瓷砖每块15元，白瓷砖每块12元，当白砖共有10横行时，共需花多少钱购买瓷砖？

查看试题解析
20. 计算

(1)、 $(a - 2 b + c) (a + 2 b - c)$ ；

(2)、已知： $x + y = 3$ ， $x y = - 7$ ，求：
① $x^{2} + y^{2}$ ；
② ${(x - y)}^{2}$ .

查看试题解析
21. 老王想靠着一面足够长的旧墙EF，开垦一块长方形的菜地ABCD，如图所示，菜地的一边靠墙，另外三边用竹篱笆围起来，并在平行于墙的一边BC上留1米宽装门，已知现有竹篱笆长共32米．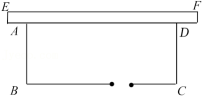

(1)、设垂直于墙面的一边AB长为 $x$ 米，则AD边的长用含 $x$ 的代数式可表示为米．

(2)、设菜地面积为S，用含 $x$ 的代数式来表示S．

(3)、当 $x$ ＝8时，菜地面积为多少平方米？

查看试题解析
22. 小红准备完成题目：计算（x² x+2）（x²﹣x）．她发现第一个因式的一次项系数被墨水遮挡住了．

(1)、她把被遮住的一次项系数猜成3，请你完成计算：（x²+3x+2）（x²﹣x）；

(2)、老师说：“你猜错了，这个题目的正确答案是不含三次项的．”请通过计算说明原题中被遮住的一次项系数是多少？

查看试题解析
23. 观察下列各式：
$(x - 1) (x + 1) = x^{2} - 1$

$(x - 1) (x^{2} + x + 1) = x^{3} - 1$

$(x - 1) (x^{3} + x^{2} + x + 1) = x^{4} - 1$

……

由上面的规律：

(1)、求 $2^{5} + 2^{4} + 2^{3} + 2^{2} + 2 + 1$ 的值；

(2)、求 $2^{2011} + 2^{2010} + 2^{2009} + 2^{2008} +$ …+2+1的个位数字．

(3)、你能用其它方法求出 $\frac{1}{2} + \frac{1}{2^{2}} + \frac{1}{2^{3}} + \dots + \frac{1}{2^{2010}} + \frac{1}{2^{2011}}$ 的值吗？

查看试题解析

鲁教版（五四制）2022-2023学年度第二学期六年级数学 整式的乘法 期中复习

一、单选题

二、填空题

三、解答题

四、综合题

鲁教版（五四制）2022-2023学年度第二学期六年级数学整式的乘法期中复习