鲁教版（五四制）2022-2023学年度第二学期六年级数学零指数幂与负整数指数幂期中复习

试卷更新日期：2023-04-17 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 ${(\frac{1}{2})}^{0} = 0$ B、（a²）³＝a⁵ C、a^﹣1÷a^﹣3＝a² D、（a+b）²＝a²+b²

查看试题解析
2. 已知 a＝2 ^{- 2} ， b＝（π－2）⁰ ， c＝（－1）³ ，则 a，b，c 的大小关系为（）

A、c＜b＜a B、b＜a＜c C、c＜a＜b D、a＜c＜b

查看试题解析
3. 下列运算中，正确的是（）

A、 $4^{- 1} = - 4$ B、 $4^{0} = 1$ C、 $\sqrt{4} = \pm 2$ D、 $| - 4 | = - 4$

查看试题解析
4. 计算 $(- 2022)^{- 1}$ 的正确结果是（）

A、 $2022$ B、 $- 2022$ C、 $\frac{1}{2022}$ D、 $- \frac{1}{2022}$

查看试题解析
5. 已知 $a^{a - 1} \div a = a$ ，则 $a =$ （）

A、3 B、1 C、 $- 1$ D、3或±1

查看试题解析
6. 我们知道…，2^-3= $\frac{1}{8}$ ， 2^-2= $\frac{1}{4}$ ， 2^-1= $\frac{1}{2}$ ， 2⁰=1，2¹=2，2²=4，2³=8，…．如果要把指数推广到有理数，则2^-0.5=（）

A、-0.5 B、2 C、 $\frac{1}{\sqrt{2}}$ D、 $\sqrt{2}$

查看试题解析
7. 根式 $\frac{1}{\sqrt[n]{a^{m}}}$ （ $a > 0$ ， $m 、 n$ 为正整数， $n$ ＞1）用分数指数幂可表示为（）

A、 $a^{\frac{n}{m}}$ B、 $a^{\frac{m}{n}}$ C、 $a^{- \frac{n}{m}}$ D、 $a^{- \frac{m}{n}}$

查看试题解析
8. 下列计算中错误的是（）

A、 $5^{2} \times 5^{9} = 5^{11}$ B、 ${(2^{2})}^{5} = 2^{10}$ C、 ${(\frac{2}{3})}^{2} = \frac{4}{3}$ D、 ${(- 15)}^{0} = 1$

查看试题解析
9. 如果a=（-10）⁰ ， b=（-0.1）^-1 ， c=（- $\frac{1}{3}$ ）^-2 ，那么a、b、c的大小关系为（）

A、a＞b＞c B、c＞a＞b C、a＞c＞b D、c＞b＞a

查看试题解析
10. 我们知道： $2^{1} = 2$ ， $2^{2} = 4$ ， ……， $2^{10} = 1024$ ，那么 $2^{- 30}$ 接近于（）

A、 $1 0^{- 10}$ B、 $1 0^{- 9}$ C、 $1 0^{- 8}$ D、 $1 0^{- 7}$

查看试题解析

二、填空题

11. 当（a- $\frac{1}{3}$ ）⁰＝1时，a的取值范围是.

查看试题解析
12. 已知 $a = {(\frac{2}{3})}^{- 2}$ ， $b = {(- 2)}^{2}$ ， $c = {(π - 2021)}^{0}$ ，则a，b，c的大小关系为．

查看试题解析
13. 计算 ${(- 2022)}^{0}$ 的结果是．

查看试题解析
14. $1 6^{- \frac{1}{2}} =$ ．

查看试题解析
15. 计算 ${(\sqrt{3})}^{0} + {(\frac{1}{2})}^{- 1} =$ .

查看试题解析

三、解答题

16. 某种液体每升含有10¹²个细菌，某种杀菌剂1滴可以杀死10⁹个此种有害细菌，现在若要将3L这种液体中的有害细菌杀死，要用这种杀菌剂多少滴？
若10滴这种杀菌剂为10^-3L，要用多少升？

查看试题解析
17. 课堂上老师出了这么一道题：（2x-3）^x+3-1=0，求x的值.小明同学解答如下：
解：∵（2x-3）^x+3-1=0，

∴（2x-3）^x+3=1.

∵（2x-3）⁰=1，

$∴$ x+3=0，

$∴$ x=-3

请问小明的解答过程正确吗？如果不正确，请求出正确的值.

查看试题解析
18. 若 ${(4 x - 3 y - 5)}^{0}$ 无意义，且3x+2y=8，求x，y的值。

查看试题解析

四、综合题

19. 已知P＝A·B-M．

(1)、若A＝(-3)⁰ ， B＝ ${(- \frac{1}{2})}^{- 1}$ ， M＝|-1|，求P的值；

(2)、若A＝3，B＝x，M＝5x-1，且P≤3，求x的取值范围，并在如图所示的数轴上表示出解集．

查看试题解析
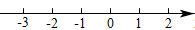20. 阅读材料：若m²﹣2mn+2n²﹣8n+16＝0，求m、n的值.
解：∵m²﹣2mn+2n²﹣8n+16＝0，
∴（m²﹣2mn+n²）+（n²﹣8n+16）＝0
（m﹣n）²+（n﹣4）²＝0，
∴（m﹣n）²＝0且（n﹣4）²＝0，
∴ m＝n＝4.
根据你的观察，探究下面的问题：

(1)、a²﹣2a+1+b²＝0，则a＝， b＝；

(2)、已知x²+2y²﹣2xy+4y+4＝0，求x^y的值；

(3)、已知△ABC的三边长a、b、c都是正整数，且满足2a²+b²﹣4a﹣10b+27＝0，求△ABC的周长.

查看试题解析
21. 规定两数 $a$ ， b之间的一种新运算※，如果 $a^{c} = b$ ，那么 $a ※ b = c$ .例如：因为 $5^{2} = 25$ ，所以 $5 ※ 25 = 2$ ，因为 $5^{0} = 1$ ，所以 $5 ※ 1 = 0$ .

(1)、根据上述规定，填空； $2 ※ 8 =$ ； $2 ※ \frac{1}{16} =$ .

(2)、在运算时，按以上规定：设 $4 ※ 5 = x$ ， $4 ※ 6 = y$ ，请你说明下面这个等式成立： $4 ※ 5 + 4 ※ 6 = 4 ※ 30$ .

查看试题解析
22. 阅读解答：

(1)、填空：2¹-2⁰=2^（^）， 2²-2¹=2^（^）， 2³-2²=2^（^）， …

(2)、探索（1）中式子的规律，试写出第n个等式.

(3)、计算：2⁰+2¹+2²+2³+2⁴+…+2¹⁰⁰⁰

查看试题解析
23.

(1)、计算：2001²-1999×2003；

(2)、计算： $(\frac{1}{3})^{0} \div (- \frac{1}{3})^{- 2} - 16 \times 2^{- 4}$

(3)、已知：x^m=3，xⁿ=2，求x^2m-3n的值．

查看试题解析

鲁教版（五四制）2022-2023学年度第二学期六年级数学 零指数幂与负整数指数幂 期中复习

一、单选题

二、填空题

三、解答题

四、综合题

鲁教版（五四制）2022-2023学年度第二学期六年级数学零指数幂与负整数指数幂期中复习